Toán 11
Phương pháp giải các dạng toán Phép tịnh tiến cực hay
Xin chào các bạn, bài học hôm nay sẽ đem đến cho các bạn nhưng phương pháp để các bạn có thể giải quyết các dạng toán phép tịnh tiến. Hãy theo dõi hết bài viết cung HocThatGioi nhé.
1. Xác định ảnh của một hình qua phép tịnh tiến
Phương pháp giải: Gọi H' là ảnh của hình H qua phép tịnh tiến theo vectơ \overrightarrow{v} = (a;b). Với mọi điểm M(x;y) bất kỳ thuộc H, ta có T_{\overrightarrow{v}}(M) = M'(x';y') \in H'
\left\{\begin{matrix}x' = x + a\\y' = y + b\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x' - a\\y = y' - b\end{matrix}\right. \Rightarrow M(x' - a;y' - b)Thay toạ độ điểm M vào phương trình biểu diễn hình H ta thu được phương trình biểu diễn hình H'.
Ví dụ 1: Trong mặt phẳng Oxy, cho \overrightarrow{v} = (2;1) và điểm M(3;2). Tìm toạ độ điểm A sao cho
a. A = T_{\overrightarrow{v}}(M)
b. M = T_{\overrightarrow{v}}(A)
a. A = T_{\overrightarrow{v}}(M)
b. M = T_{\overrightarrow{v}}(A)
a. A = T_{\overrightarrow{v}}(M)
Giả sử A(x;y) ta có A = T_{\overrightarrow{v}}(M) \Rightarrow \left\{\begin{matrix}x = 3 + 2\\y = 2 + 1\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = 5\\y = 3\end{matrix}\right. \Rightarrow A(5;3)
b. M = T_{\overrightarrow{v}}(A)
Giả sử A(x;y) ta có M = T_{\overrightarrow{v}}(A) \Rightarrow \left\{\begin{matrix}3 = x + 2\\2 = y + 1\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = 1\\y = 1\end{matrix}\right. \Rightarrow A(1;1)
Giả sử A(x;y) ta có A = T_{\overrightarrow{v}}(M) \Rightarrow \left\{\begin{matrix}x = 3 + 2\\y = 2 + 1\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = 5\\y = 3\end{matrix}\right. \Rightarrow A(5;3)
b. M = T_{\overrightarrow{v}}(A)
Giả sử A(x;y) ta có M = T_{\overrightarrow{v}}(A) \Rightarrow \left\{\begin{matrix}3 = x + 2\\2 = y + 1\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = 1\\y = 1\end{matrix}\right. \Rightarrow A(1;1)
Ví dụ 2: Trong mặt phẳng Oxy, cho đường thẳng d. Hãy tìm ảnh của đường thẳng d qua phép tịnh tiến theo vectơ \overrightarrow{v}
a. d: 2x – 3y + 12 = 0, \overrightarrow{v} = (4;3)
b. d: 2x + y – 12 = 0, \overrightarrow{v} = \overrightarrow{AB}, A(3;1), B(-1;8)
a. d: 2x – 3y + 12 = 0, \overrightarrow{v} = (4;3)
b. d: 2x + y – 12 = 0, \overrightarrow{v} = \overrightarrow{AB}, A(3;1), B(-1;8)
Gọi d’ là ảnh của đường thẳng d qua phép tịnh tiến theo vectơ \overrightarrow{v}; M(x;y) là một điểm bất kì trên đường thẳng d và M(x’;y’) = T_{\overrightarrow{v}}(M). Khi đó:
a. d: 2x – 3y + 12 = 0, \overrightarrow{v} = (4;3)
\left\{\begin{matrix}x’ = x + 4\\y’ = y – 3\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x’ – 4\\y = y’ + 3\end{matrix}\right. \Rightarrow M(x’ – 4;y’ + 3). Ma điêm M thuộc đường thẳng d nên:
2(x’ – 4) – 3(y’ + 3) + 12 = 0 \Leftrightarrow 2x’ – 3y’ – 5 = 0
Suy ra phương trình đường thẳng d’ là 2x – 3y – 5 = 0
b. d: 2x + y – 12 = 0, \overrightarrow{v} = \overrightarrow{AB}, A(3;1), B(-1;8)
Ta có: \overrightarrow{v} = \overrightarrow{AB} = (-4;7). Do đó
\left\{\begin{matrix}x’ = x – 4\\y’ = y + 7\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x’ + 4\\y = y’ – 7\end{matrix}\right. \Rightarrow M(x’ + 4;y’ – 7). Mà điêm M thuộc đường thẳng d nên:
2(x’ + 4) – 3(y’ – 7) – 4 = 0 \Leftrightarrow 2x’ + y’ – 3 = 0
Suy ra phương trình đường thẳng d’ là 2x’ + y’ – 3 = 0
a. d: 2x – 3y + 12 = 0, \overrightarrow{v} = (4;3)
\left\{\begin{matrix}x’ = x + 4\\y’ = y – 3\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x’ – 4\\y = y’ + 3\end{matrix}\right. \Rightarrow M(x’ – 4;y’ + 3). Ma điêm M thuộc đường thẳng d nên:
2(x’ – 4) – 3(y’ + 3) + 12 = 0 \Leftrightarrow 2x’ – 3y’ – 5 = 0
Suy ra phương trình đường thẳng d’ là 2x – 3y – 5 = 0
b. d: 2x + y – 12 = 0, \overrightarrow{v} = \overrightarrow{AB}, A(3;1), B(-1;8)
Ta có: \overrightarrow{v} = \overrightarrow{AB} = (-4;7). Do đó
\left\{\begin{matrix}x’ = x – 4\\y’ = y + 7\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x’ + 4\\y = y’ – 7\end{matrix}\right. \Rightarrow M(x’ + 4;y’ – 7). Mà điêm M thuộc đường thẳng d nên:
2(x’ + 4) – 3(y’ – 7) – 4 = 0 \Leftrightarrow 2x’ + y’ – 3 = 0
Suy ra phương trình đường thẳng d’ là 2x’ + y’ – 3 = 0
Ví dụ 3: Trong mặt phẳng Oxy, cho đường tròn (C). Hãy tìm ảnh của đường tròn (C) qua phép tịnh tiến \overrightarrow{v}, biết
a: (C) : (x – 4)^{2} + (y + 3)^{2} = 6, \overrightarrow{v} = (3;2)
b: (C) : x^{2} + y^{2} + 4x – 4y – 1 = 0, \overrightarrow{v} = \overrightarrow{AB} với A(-1;1), B(1;-2)
a: (C) : (x – 4)^{2} + (y + 3)^{2} = 6, \overrightarrow{v} = (3;2)
b: (C) : x^{2} + y^{2} + 4x – 4y – 1 = 0, \overrightarrow{v} = \overrightarrow{AB} với A(-1;1), B(1;-2)
Gọi (C)’ là ảnh của đương tròn (C) qua phép tịnh tiến theo vectơ \overrightarrow{v}, M(x;y) là một điểm bất kì trên đườn tròn (C) và M(x’;y’) = T_{\overrightarrow{v}}(M). Khi đó:
a: (C) : (x – 4)^{2} + (y + 3)^{2} = 6, \overrightarrow{v} = (3;2)
\left\{\begin{matrix}x’ = x + 3\\y’ = y + 2\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x’ – 3\\y = y’ – 2\end{matrix}\right. \Rightarrow M(x’ – 3;y’ – 2). Mà điêm M thuộc đường tròn (C) nên:
(x’ – 3 – 4)^{2} + (y’ -2 + 3)^{2} = 6 \Leftrightarrow (x’ – 7)^{2} – (y’ + 1)^{2} = 6
Phương trình đường tròn (C) là (x’ – 7)^{2} – (y’ + 1)^{2} = 6
b: (C) : x^{2} + y^{2} + 4x – 4y – 1 = 0, \overrightarrow{v} = \overrightarrow{AB} với A(-1;1), B(1;-2)
Ta có \overrightarrow{v} = \overrightarrow{AB} = (2;-3)
\left\{\begin{matrix}x’ = x + 2\\y’ = y – 3\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x’ – 2\\y = y’+ 3\end{matrix}\right. \Rightarrow M(x’ – 2;y’ + 3). Mà điêm M thuộc đường tròn (C) nên:
(x’ – 2)^{2} + (y’ + 3)^{2} + 4(x’ – 2) – 4(y’ – 3) – 1= 0 \Leftrightarrow x’^{2} + y’^{2} + 2y’ + 16= 0
Phương trình đường tròn (C) là x’^{2} + y’^{2} + 2y’ + 16= 0
a: (C) : (x – 4)^{2} + (y + 3)^{2} = 6, \overrightarrow{v} = (3;2)
\left\{\begin{matrix}x’ = x + 3\\y’ = y + 2\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x’ – 3\\y = y’ – 2\end{matrix}\right. \Rightarrow M(x’ – 3;y’ – 2). Mà điêm M thuộc đường tròn (C) nên:
(x’ – 3 – 4)^{2} + (y’ -2 + 3)^{2} = 6 \Leftrightarrow (x’ – 7)^{2} – (y’ + 1)^{2} = 6
Phương trình đường tròn (C) là (x’ – 7)^{2} – (y’ + 1)^{2} = 6
b: (C) : x^{2} + y^{2} + 4x – 4y – 1 = 0, \overrightarrow{v} = \overrightarrow{AB} với A(-1;1), B(1;-2)
Ta có \overrightarrow{v} = \overrightarrow{AB} = (2;-3)
\left\{\begin{matrix}x’ = x + 2\\y’ = y – 3\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = x’ – 2\\y = y’+ 3\end{matrix}\right. \Rightarrow M(x’ – 2;y’ + 3). Mà điêm M thuộc đường tròn (C) nên:
(x’ – 2)^{2} + (y’ + 3)^{2} + 4(x’ – 2) – 4(y’ – 3) – 1= 0 \Leftrightarrow x’^{2} + y’^{2} + 2y’ + 16= 0
Phương trình đường tròn (C) là x’^{2} + y’^{2} + 2y’ + 16= 0
2. Xác định phép tịnh tiến khi biết ảnh và tạo ảnh
Phương pháp giải: Giả sử M'(x';y') là ảnh của M(x;y) qua phép tịnh tiến thepo vectơ \overrightarrow{v} = (a;b). Khi đó, ta có \overrightarrow{v} = \overrightarrow{MM'} và toạ độ \overrightarrow{v} được xác định như sau: \left\{\begin{matrix}a = x' - x\\b = y' - y\end{matrix}\right.
Ví dụ 1: Trong mặt phẳng Oxy. cho một phép tịnh tiến biến đường tròn (C): (x + 1)^{2} + (y – 2)^{2} = 16 thành đường tròn (C’): (x – 10)^{2} + (y + 5)^{2} = 16. Hãy xác định phép tịnh tiến đó.
Từ phương trình đường tròn (C) và (C’), ta suy ra tâm hai đường tròn lần lượt là I(-1;2), I'(10;-5). Ta có T_{\overrightarrow{v}}(C) = C’ \Rightarrow T_{\overrightarrow{v}}(I) = I’ \Rightarrow \overrightarrow{v} = \overrightarrow{II’} = (11;-7)
Ví dụ 2: Trong mặt phẳng Oxy, cho hai đường thẳng lần lượt có phương trình d: 3x – 5y + 3 = 0 và d’: 3x – 5y + 24 = 0. Tìm \overrightarrow{v} có giá vuông góc với đường thẳng d để d’ là ảnh của d qua T_{\overrightarrow{v}}
Chọn điểm A(0;1) \in d. Gọi \Delta là đường thẳng đi qua A và vuông góc với d \Rightarrow \Delta: 3x + 2y – 2 = 0
Gọi A’ = b’ \cap \Delta. Toạ độ điểm A’ thoả mãn hệ phương trình
\left\{\begin{matrix}2x – 3y – 5 = 0\\3x + 2y – 2 = 0\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = \frac{16}{13}\\ \frac{11}{13}\end{matrix}\right.
Vậy \overrightarrow{v} = \overrightarrow{AA’} = (\frac{16}{13};\frac{-24}{13})
Gọi A’ = b’ \cap \Delta. Toạ độ điểm A’ thoả mãn hệ phương trình
\left\{\begin{matrix}2x – 3y – 5 = 0\\3x + 2y – 2 = 0\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x = \frac{16}{13}\\ \frac{11}{13}\end{matrix}\right.
Vậy \overrightarrow{v} = \overrightarrow{AA’} = (\frac{16}{13};\frac{-24}{13})
3. Dùng phép tịnh tiến để giải các bài toán dựng hình
Phương pháp giải:
- Để dựng một điểm M ta tìm cách xem nó là ảnh của một điểm đã biết qua một phép tịnh tiến, hoặc xem M là giao điểm của hai đường trong đó một đường cố định còn một đường là ảnh của một đường đã biết qua phép tịnh tiến.
- Sử dụng kết quả: Nếu T_{\overrightarrow{v}}(N)=M, N∈(H) thì M \in (H′), trong đó (H′)=T_{\overrightarrow{v}}((H)) và kết hợp với M thuộc hình (K) (theo giả thiết) để suy ra M \in (H') \cap (K)
Ví dụ: Cho đường tròn tâm O, bán kính R và hai điểm phân biệt C, D nằm ngoài (O). Hãy dựng dây cung AB của đường tròn (O) sao cho ABCD là hình bình hành
Phân tích: Gỉa sử dựng được dây cung AB thoả mãn yêu cầu bài toán
Do ABCD là hình bình hành nên \overrightarrow{AB} = \overrightarrow{DC} \Rightarrow T_{\overrightarrow{CD}}(A) = B
Nhưng A \in (O) \Rightarrow B \in (O’) = T_{\overrightarrow{DC}}((O)). Vậy B vừa thuộc (O), (O’) nên B chình là giao điểm của (O), (O’)
Cách dựng:
+Dựng đường tròn (O’) là ảnh của đường tròn (O) qua T_{\overrightarrow{DC}}
+ Dựng giao điểm B của (O) và (O’)
+ Dựng đường thẳng qua B và song song với CD cắt (O) tại A
Dây cung AB là dây cung thỏa yêu cầu bài toán.
Chứng minh: Từ các dựng ta có T_{\overrightarrow{DC}}(A) = B \Rightarrow \overrightarrow{AB} = \overrightarrow{DC} \Rightarrow ABCD là hình bình hành.
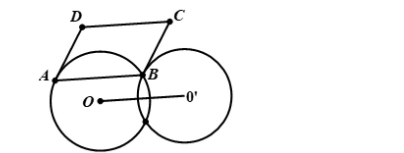
Do ABCD là hình bình hành nên \overrightarrow{AB} = \overrightarrow{DC} \Rightarrow T_{\overrightarrow{CD}}(A) = B
Nhưng A \in (O) \Rightarrow B \in (O’) = T_{\overrightarrow{DC}}((O)). Vậy B vừa thuộc (O), (O’) nên B chình là giao điểm của (O), (O’)
Cách dựng:
+Dựng đường tròn (O’) là ảnh của đường tròn (O) qua T_{\overrightarrow{DC}}
+ Dựng giao điểm B của (O) và (O’)
+ Dựng đường thẳng qua B và song song với CD cắt (O) tại A
Dây cung AB là dây cung thỏa yêu cầu bài toán.
Chứng minh: Từ các dựng ta có T_{\overrightarrow{DC}}(A) = B \Rightarrow \overrightarrow{AB} = \overrightarrow{DC} \Rightarrow ABCD là hình bình hành.
4. Sử dụng phép tịnh tiến để giải các bài toán tìm tập hợp điểm
Phương pháp: Nếu T_{\overrightarrow{v}}(M) = M' và điểm M di động trên hình (H) thì điểm M' thuộc hình (H'), trong đó (H') là ảnh của hình (H) qua T_{\overrightarrow{v}}
Ví dụ: Cho hai điểm phân biệt B, C cố định trên đường tròn (O) tâm O. Điểm A di động trên (O). Chứng minh khi A di động trên (O) thì trực tâm của tam giác ABC di động trên một đường tròn
Gọi H là trực tâm của tam giác ABC và M là trung điểm của BC. Tia BO cắt đường tròn (O) tại D
Vì \widehat{BCD} = 90^{\circ} nên DC\\AH. Tương tự AD\\CH
Do đó ADCH là hình bình hành
Suy ra \overrightarrow{AH} = \overrightarrow{DC} = 2\overrightarrow{OM} không đổi.
\Rightarrow T_{2\overrightarrow{OM}}(A) = H.
Vì vậy khi A di động trên đường tròn (O) thì H di động trên đường tròn (O’) = T_{2\overrightarrow{OM}}(O)
Vì \widehat{BCD} = 90^{\circ} nên DC\\AH. Tương tự AD\\CH
Do đó ADCH là hình bình hành
Suy ra \overrightarrow{AH} = \overrightarrow{DC} = 2\overrightarrow{OM} không đổi.
\Rightarrow T_{2\overrightarrow{OM}}(A) = H.
Vì vậy khi A di động trên đường tròn (O) thì H di động trên đường tròn (O’) = T_{2\overrightarrow{OM}}(O)
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Phương pháp giải các dạng toán Phép tịnh tiến cực hay. Nếu thấy bài viết hay, bổ ích hãy chia sẻ nó đến với bạn bè của mình và đừng quên theo dõi HocThatGioi để cập nhật nhiều kiến thức hay mỗi ngày nhé! Chúc các bạn học tốt!
