Phương pháp giải hình nón ngoại tiếp nội tiếp hình trụ chi tiết nhất

Quang Thái Tháng Mười Hai 6, 2021

Xin chào các bạn, sau khi đã hoàn thành thành bài Phương pháp giải hình nón ngoại tiếp nội tiếp hình chóp. Hôm nay HocThatGioi sẽ đem đến cho các bạn Phương pháp giải hình nón ngoại tiếp nội tiếp hình trụ cũng như một số ví dụ giúp các bạn nắm vững kiến thức nhé.

1. Phương pháp giải hình nón ngoại tiếp hình trụ

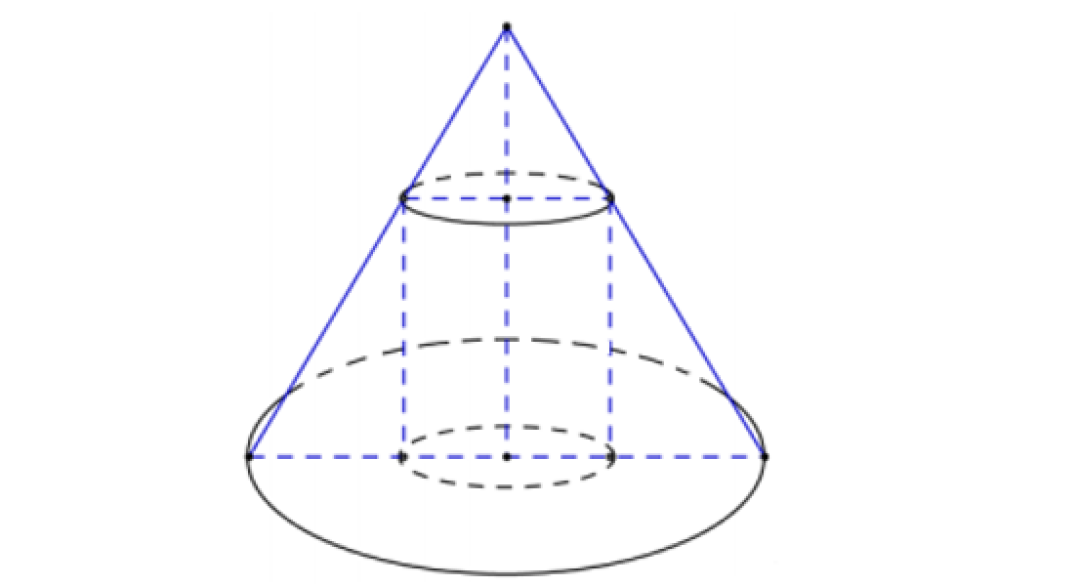
Hình nón ngoại tiếp hình trụ (hình trụ nội tiếp hình nón) thì hình trụ có một đáy nằm trong đáy hình nón, đáy còn lại là thiết diện của mặt phẳng vuông góc với trục của hình nón với hình nón

Phương pháp giải:

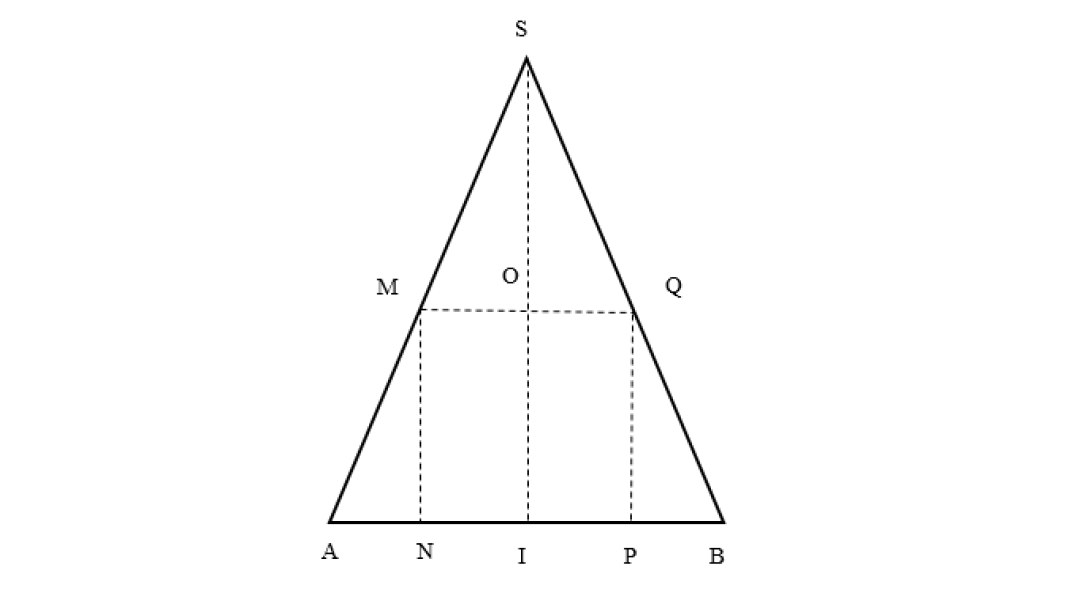
Xét mặt cắt qua trục, ta đưa về bái toán tam giác ngoại tiếp hình chữ nhật, cụ thể $\Delta SAB$ (thiết diện qua trục hình nón) và hình chữ nhật $MNPQ$ (thiết diện qua trục hình trụ)

Gọi $R, h, R', h'$ lần lượt là bán kính đáy và chiều cao của hình nón; bán kính đáy và chiều cao hình trụ :

Ta có : $R = IA; h = SI, R' = IN; h' = OI$

Lưu ý: Ta có

\Delta AMN \backsim \Delta ASI => \frac{MN}{SI} = \frac{AN}{AI} => \frac{h’}h{} = \frac{R – R’}{R}

Ví dụ minh hoạ 1:

Cho hình nón có bán kính đáy R và đường sinh tạo với mặt đáy một góc

60^{\circ}

và một hình trụ nội tiếp hình nón, biết bán kính của hình trụ bằng một nửa bán kính đáy của hình nón. Tính thể tích khối trụ.

Do bán kính của trụ bằng một nửa bán kính đáy của nón nên mặt đáy của hình trụ là thiết diện tạo bởi hình nón và mặt phẳng đi qua trung điểm đường sinh của hình nón và vuông góc với trục của hình nón. Độ dài đường cao của nón

h = \frac{R\sqrt{3}}{2}

nên đường cao trụ bằng

h = \frac{R\sqrt{3}}{4}

.
Vậy

V = \pi r^{2}h = \pi\frac{R^{3}\sqrt{3}}{16}

Ví dụ minh hoạ 2:

Cho một hình nón đỉnh

S

, mặt đáy là hình tròn tâm

O

, bán kính

R = 6cm

và có thiết diện qua trục là tam giác đều. Cho một hình trụ có hai đường tròn đáy là

(O; r)

và

(I; r)

, có thiết diện qua trục là hình vuông, biết đường tròn

(O; r)

nằm trên mặt đáy của hình nón, đường tròn

(I; r)

nằm trên mặt xung quanh của hình nón (

I

thuộc đoạn

SO

). Tính thể tích khối trụ.

Hình nón có bán kính đường tròn đáy

R = 6cm

và có thiết diện qua trục là tam giác đều, nên có :

SM = 2R = 12 cm, SO = SM\frac{\sqrt{3}}{2} = 6\sqrt{3}

Đặt

SI = x

, vì

BI // AO

nên ta có:

\frac{BI}{OM} = \frac{SI}{SO} => \frac{r}{6} = \frac{x}{6\sqrt{3}} => r = \frac{x}{\sqrt{3}}

.
Chiều cao của hình trụ là :

h = OI = SO – SI = 6\sqrt{3} – x

.
Do đó thiết diện qua trục của hình trụ là hình vuông khi và chỉ khi:

h = 2r \Leftrightarrow 6\sqrt{3} – x = \frac{2x}{\sqrt{3}} => x = 18(2 – \sqrt{3})

Khi đó :

h = 12(2\sqrt{3} -3); r = \frac{h}{2} = 6(2\sqrt{3} -3)

Vậy

V = \pi r^{2}h = 1296\pi(26\sqrt{3} -45)

Phương pháp giải hình nón ngoại tiếp nội tiếp hình trụ chi tiết nhất 9

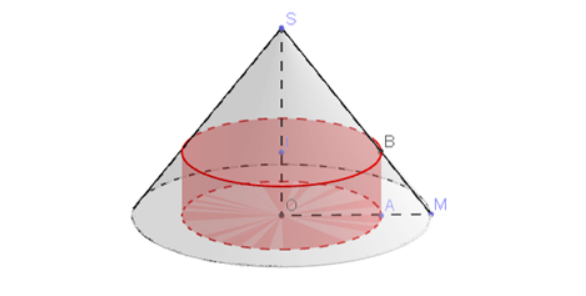
2. Phương pháp giải hình nón nội tiếp hình trụ

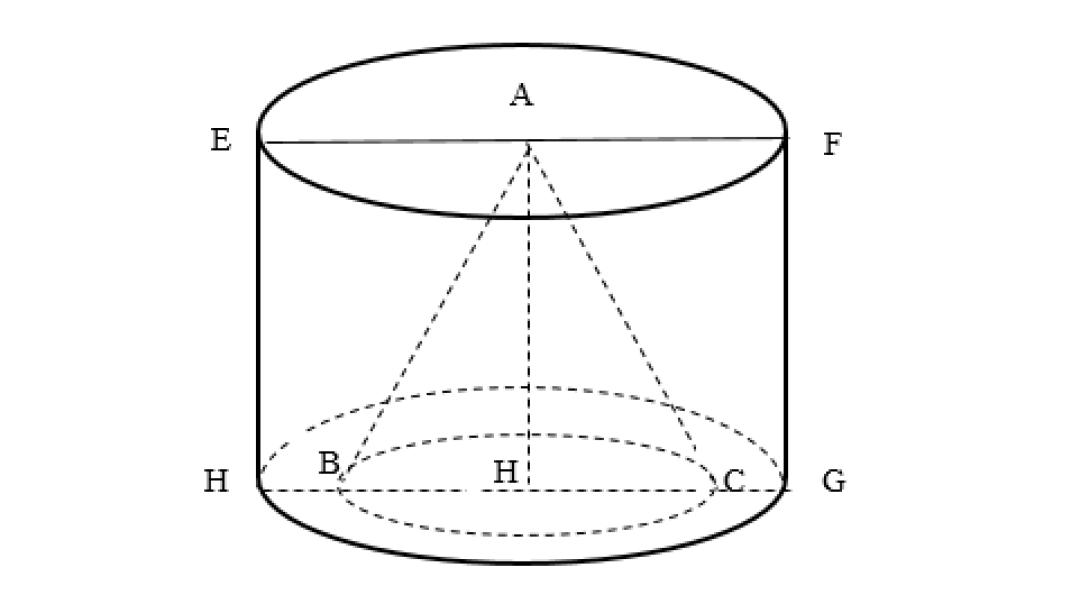
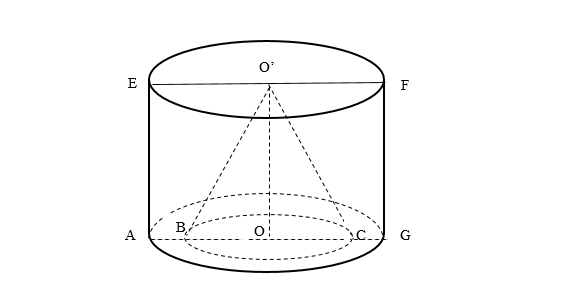
Hình nón nội tiếp hình trụ (hình trụ ngoại tiếp hình nón) thì hình nón có đáy nằm trong đáy của hình tụ, đỉnh thuộc mặt đáy trên của hình trụ.

Phương pháp giải:

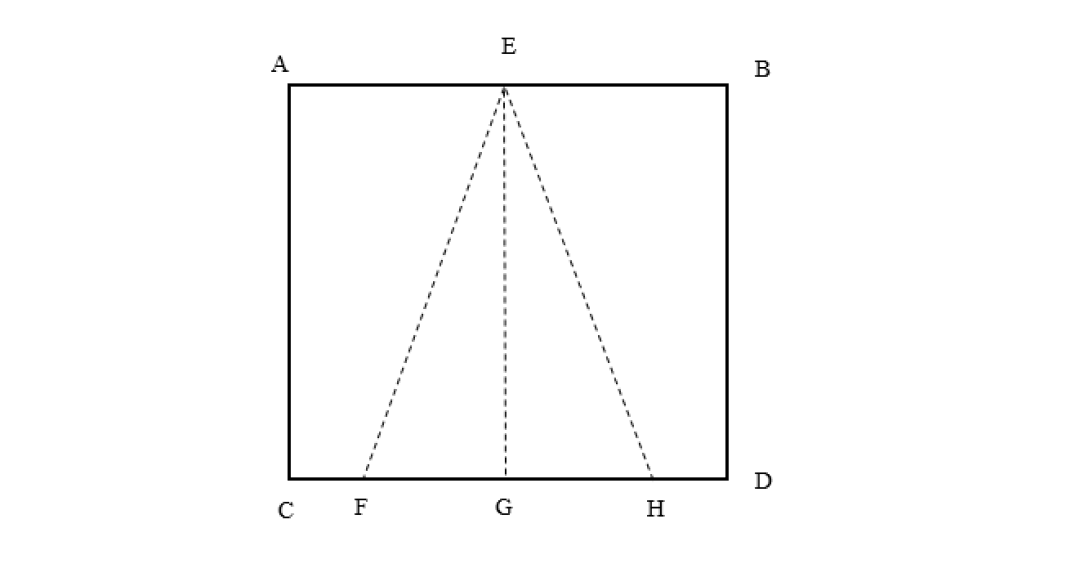
Xét mặt cắt qua trục, ta đưa về bái toán tam giác nội tiếp hình chữ nhật, cụ thể $\Delta EFH$ (thiết diện qua trục hình nón) và hình chữ nhật $ABCD$ (thiết diện qua trục hình trụ).

Gọi $R, h, R', h'$ lần lượt là bán kính đáy và chiều cao của hình nón; bán kính đáy và chiều cao hình trụ :

Ta có: $R = GH, h = EG, R' = GD, h' = EG$

Ví dụ minh hoạ:

Cho hình trụ có chiều

OO’ = h = 6cm

. Tính diện tích xung của của hình nón có đỉnh

O’

, đáy là đường tròn trong đáy của hình trụ có tâm

O

bán kính

r = 3 cm

Ta có

OO’ = 6 cm, OC = 3 cm

=> l = OC = \sqrt{r^{2} + h^{2}} = \sqrt{OO’^{2} + OC^{2}} = 3\sqrt{5} cm

Vậy

S_{xq} = \pi rl = \pi 3.3\sqrt{5} = 9\pi\sqrt{5}

Phương pháp giải hình nón ngoại tiếp nội tiếp hình trụ chi tiết nhất 12

Xin cảm ơn các bạn đã theo dõi hết bài viết hôm nay. Qua bài viết này, Các bạn cùng theo dõi các bài viết tiếp theo về chương Mặt tròn xoay để có một nền tảng thật vững chắc nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt.