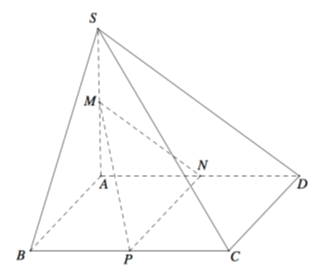
Vị trí tương đối của hai đường thẳng trong không gian siêu dễ.
Xin chào các bạn, bài học hôm nay HocThatGioi sẽ giới thiệu tới các bạn các vị trí tương đối của 2 đường thẳng trong không gian. Đây là một chuyên đề rất quan trong trong chương trình Hình học 11. Với bài học hôm nay các bạn có thể nắm được các kiến thức cơ bản về vị trí tương đối của hai đường thẳng trong không gian cũng như làm được những câu nhận biết trị trí tương đối giữa 2 đường thẳng trong không gian. Hãy cùng mình tìm hiểu nhé.
1.Vị trí tương đối của hai đường thẳng trong không gian
a. Hai đường thẳng đồng phẳng
Trong trường hợp này vị trí tương đối của 2 đường thẳng là những vị trí đã học ở cấp 2.
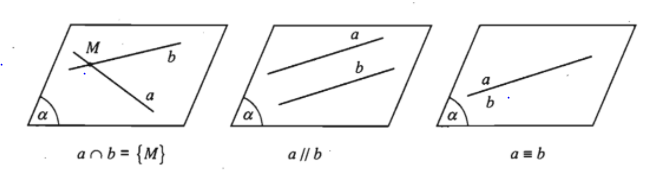
- Đường thẳng a và b cắt nhau khi chúng có 1 điểm chung. Ký hiệu là a\cap b={M}.
- Đường thẳng a và b cắt nhau khi chúng không có điểm chung . Ký hiệu là a//b.
- Đường thẳng a và b cắt nhau khi chúng có vô số điểm chung. Ký hiệu là a\equiv b.
b.Hai đường thẳng chéo nhau
Hai đường thẳng chéo nhau khi chúng không thuộc cùng một mặt phẳng hay không có mặt phẳng nào chứa hai đường thẳng đó.
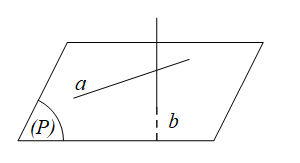
2. Một số tính chất của 2 đường thẳng song song
Có 2 tính chất quan trọng của 2 đường thẳng trong không gian mà các bạn cần lưu ý:
- Tính chất 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.
- Tính chất 2: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Định lí: (về giao tuyến của hai mặt phẳng) Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.
Hệ quả: Nếu hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).
3. Bài tập vận dụng
Cảm ơn các bạn đã theo dõi hết bài viết trên của HocThatGioi. Nếu thấy bài viết này hay và bổ ích hãy chia sẻ nó đến với bạn bè của mình để cùng nhau học thật giỏi nhé! Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 12 – Toán – Phương trình đường thẳng trong không gian
- Phương trình đường thẳng, mặt phẳng và mặt cầu trong không gian Oxyz hay chi tiết nhất
- Phương trình đường thẳng trong không gian Oxyz – Góc và khoảng cách giữa đường thẳng
- Cách tính khoảng cách giữa 2 đường thẳng trong không gian Oxyz – bài tập áp dụng
- Cách viết phương trình đường thẳng trong không gian Oxyz – bài tập áp dụng
- Hình chiếu vuông góc của điểm lên đường thẳng lên mặt phẳng trong không gian Oxyz
- Quan hệ vuông góc và song song của đường thẳng, mặt phẳng trong không gian
- Vị trí tương đối của đường thẳng và mặt phẳng trong không gian siêu chi tiết.
- Góc giữa đường thẳng và mặt phẳng cực chi tiết và dễ hiểu.
- Cách tính khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian Oxyz-bài tập áp dụng
- Cách tính góc giữa 2 đường thẳng trong không gian Oxyz – bài tập áp dụng
- Cách tính góc giữa đường thẳng và mặt phẳng trong không gian Oxyz – bài tập áp dụng
- Vị trí tương đối của đường thẳng và mặt phẳng với mặt cầu trong không gian Oxyz