Lý thuyết về số phức chi tiết nhất

Ngọc Quốc Tháng Năm 8, 2021

Lý thuyết về số phức, khái niệm, biểu diễn hình học, các phép tính trong số phức, mô đun của số phức, số phức liên hợp, căn bậc 2, các lý thuyết nâng cao của số phức, 10 dạng bài tập cơ bản thường gặp

Hôm nay, HocThatGioi và các bạn sẽ cùng tìm hiểu về một dạng số mới – đó là số phức. Đây là một kiến thức mới mà có lẽ ta chưa gặp phải ở các bài trước nhưng chắc hẳn rằng khi ta bấm máy tính tìm nghiệm của phương trình thì đã bắt gặp nghiệm có dạng như $a+bi$ , ta sẽ không cho đây là nghiệm của phương trình nhưng thực ra đây chính là 1 nghiệm của phương trình ở dạng số phức đấy. Vậy số phức là gì? Ngay bây giờ hãy cùng HocThatGioi tìm hiểu ngay về bài Lý thuyết về số phức chi tiết nhất nhé!

1. Khái niệm số phức

Số phức (dạng đại số) sẽ có dạng: $z=a+bi$ , trong đó $a,b$ là các số nguyên, $a$ được gọi là phần thực, $b$ được gọi là phần ảo. Và $i$ được xem là đơn vị ảo, qui ước $i^2=-1$

Tập hợp số phức được kí hiệu là $C$ .

Nếu $z$ là số thực thì phần ảo $b=0$ , ngược lại, nếu $z$ là số thuần ảo thì phần thực của $z$ là $a=0$ .

Xét hai số phức $z = a + bi$ và $z' = a' + b'i$ , đối với số phức, ta chỉ xét xem hai số phức có bằng nhau hay không. Điều kiện 2 số phức bằng nhau $z=z'$ khi và chỉ khi $a=a'$ , $b=b'$ .

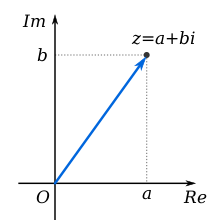
2. Biểu diễn hình học của số phức

Cho số phức $z = a + bi$ ( $a,b$ nguyên). Xét trong mặt phẳng phức $Oxy$ , $z$ sẽ được biểu diễn bởi điểm $M(a;b)$ hoặc bởi vector $u = (a;b)$ . Chú ý ở mặt phẳng phức, trục $Ox$ còn được gọi là trục thực, trục $Oy$ gọi là trục ảo.

Lý thuyết về số phức chi tiết nhất 5 — Biểu diễn hình học của số phức

3. Phép tính trong số phức:

Cho 2 số phức $A=a_1+a_2i(a_1,a_2),B=b_1+b_2i(b_1,b_2)$ . Ta có có phép tính sau:

Lý thuyết về số phức chi tiết nhất 6 — Các phép tính với số phư

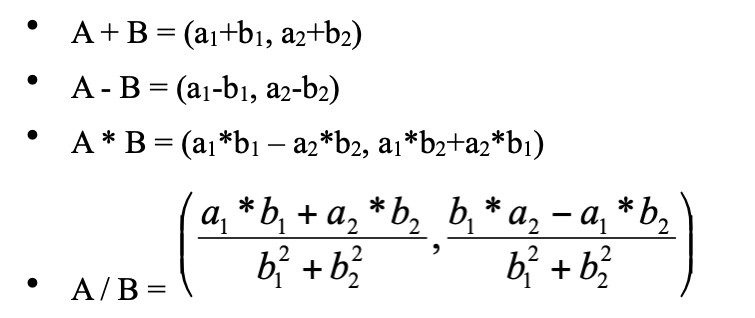
4. Mô đun của số phức

Cho số thực $z=a+bi$

Mô đun của số phức z được kí hiệu là $|z|$ và được tính: $|z|=\sqrt{a^2+b^2}$

5. Số phức liên hợp

Cho số phức $z=a+bi$

Ta có $z'=a-bi$ được gọi là số phức liên hợp của số phức z, và được kí hiệu là $\overline{z}$

Tính chất: $|\overline{z}|=|z|$

6. Căn bậc 2 của số phức

Cho số phức $z=a+bi$

Số phức $w=x+yi$ là căn bậc 2 của số phức $z$

<=> $w^2=z$

<=> $x^2-y^2=a$

và $2xy=b$

Lưu ý:

z=0

có đúng một căn bậc 2 là

w=0

z\ne0

có 2 căn bậc 2 đối nhau

7. Các lý thuyết số phức nâng cao

Lý thuyết về số phức chi tiết nhất 8 — Các lý thuyết số phức nâng cao

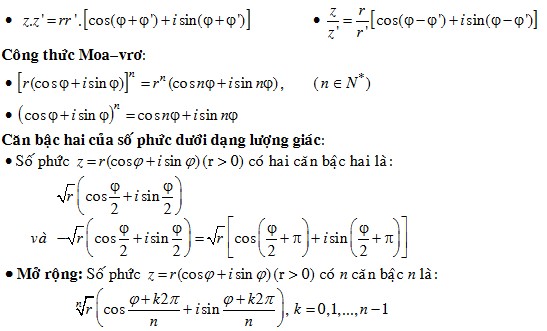
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Lý thuyết về số phức chi tiết nhất. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!