Lý thuyết về tích phân – các phương pháp giải tích phân chi tiết nhất
Lý thuyết về tích phân,tích phân là gì, tích chất của tích phân, các dạng bài thường gặp và phương pháp giải tích phân nhanh gọn chi tiết nhất
Ở bài trước, HocThatGioi đã cùng các bạn tìm hiểu chi tiết về nguyên hàm, trong bài hôm nay, chúng ta sẽ tiếp tục tìm hiểu Lý thuyết về tích phân, các phương pháp giải tích phân chi tiết nhất nhé! Đây là chủ đề khá đa dạng về dạng bài và phương pháp giải. bài viết này sẽ giúp các bạn nhận dạng được các dạng bài cũng như các phương pháp giải nhanh gọn nhất. Cùng HocThatGioi bắt đầu bài học ngay nào!
1. Lý thuyết về tích phân
1.1 Tích phân là gì?
Cho hàm số y=f(x) xác định và liên tục trên đoạn [a;b] và F(x) là một nguyên hàm nào đó của hàm số y=f(x) trên [a;b]. Khi đó:
\int_{a}^{b}f(x)dx=F(x)|^b_a=F(b)-F(a)
1.2 Tính chất của tích phân
Các tính chất của tích phân cần phải lưu ý :
\int _a^b f(u).u'(x)dx=\int _{u(a)}^{u(b)}f(u)du
2. Phương pháp giải tích phân
Có 3 phương pháp thường được sử dụng để giải tích phân:
2.1 Phương pháp tính tích phân trực tiếp
Đây là phương pháp đơn giản nhất, ta sẽ dùng các công thức nguyên hàm đã học ở bài trước để giải và tính kết quả
Ví dụ:
\int_{1}^{2}3x^2dx.
=x^3|^2_1 .
=2^3-1^3 .
=7 .
2.2 Phương pháp dùng đổi biến để tính tích phân
Đây là một phương pháp khá phổ biến trong các dạng bài tích phân:
\int _a^b f(u).u'(x)dx=\int _{u(a)}^{u(b)}f(u)du
Một số dạng tích phân đổi biến thường gặp và cách đổi biến sao cho nhanh nhất có thể

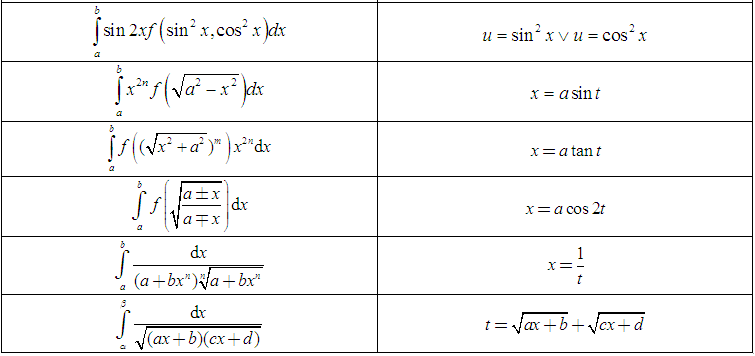
2.3 Phương pháp dùng từng phần để tính tích phân
Các dạng bài tập tích phân cần sử dụng tích phân từng phần khi hàm số dưới dấu tích phân thuộc một trong các loại: Đa thức-lượng giác; Đa thức-mũ; Logarit-đa thức; Mũ-lượng giác. Và tích phân đó không sử dụng được hoặc khó sử dụng phương pháp đổi biến.
Công thức tích phân từng phần:
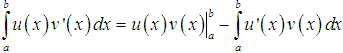
3. Các dạng bài tập về tích phân
Dạng toán 1. Tìm tích phân dựa vào tính chất của tích phân.
- Áp dụng tính chất để giải.
- Áp dụng bảng công thức cơ bản.
Dạng toán 2. Tìm tích phân của hàm số hữu tỷ.
Dạng toán 3. Giải tích phân bằng phương pháp vi phân.
Dạng toán 4. Giải tích phân bằng phương pháp đổi biến số.
- Hàm số chứa căn thức.
- Hàm số chứa hàm lượng giác.
- Hàm số chứa hàm số mũ, logarit.
- Hàm số chứa hàm số đa thức, hửu tỉ.
- Hàm số chứa hàm số không tường minh (hàm ẩn).
Dạng toán 5. Tính tích phân bằng phương pháp từng phần.
- Hàm số tường minh.
- Hàm số không tường minh (hàm ẩn).
Dạng toán 6. Tính tích phân bằng cách kết hợp nhiều phương pháp.
Dạng toán 7. Tính tích phân của các hàm số khác
- Tích phân của hàm số chứa dấu giá trị tuyệt đối.
- Tích phân của hàm số cho bởi nhiều công thức.
- Tích phân của hàm số chẵn, lẻ.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Lý thuyết về tích phân, các phương pháp giải tích phân chi tiết nhất. Nếu các bạn thấy hay và bổ ích, hãy chia sẻ cho bạn bè của mình để cùng nhau học thật giỏi. Đừng quên để lại 1 like, 1 cmt dể tạo động lực cho HocThatGioi và giúp HocThatGioi ngày càng phát triển hơn nhé! Chúc các bạn học thật tốt!
Bài viết khác liên quan đến Lớp 12 – Toán – Tích phân
- Tổng hợp tài liệu nguyên hàm – tích phân cực hay và hữu ích
- Khái niệm và các tính chất của tích phân đầy đủ nhất
- 20 câu bài tập tích phân cơ bản có lời giải chi tiết
- 20 câu bài tập tích phân hàm số hữu tỉ có lời giải chi tiết nhất
- 20 câu bài tập tích phân đổi biến số cơ bản có lời giải chi tiết nhất
- Phương pháp giải tích phân hàm số hữu tỉ hay nhất
- 20 câu bài tập tích phân từng phần có lời giải chi tiết nhất
- Phương pháp giải và bài tập tích phân chứa dấu giá trị tuyệt đối cực hay
- Tính tích phân hàm lượng giác bằng phương pháp đổi biến số cực hay
- Tổng hợp bài tập tích phân lượng giác cực hay có lời giải chi tiết
- Phương pháp tính tích phân bằng phương pháp đổi biến số hay nhất
- 10 câu bài tập tích phân hàm ẩn cực hay có lời giải chi tiết
- Tổng hợp bài tập ứng dụng tích phân để tìm diện tích có lời giải chi tiết
- Tổng hợp bài tập tập ứng dụng tích phân tính thể tích có lời giải cực hay
- Tổng hợp bài tập tích phân đổi biến số khó có lời giải chi tiết
- Phương pháp giải tích phân từng phần hay nhất
- Tính tích phân hàm lượng giác bằng phương pháp từng phần cực hay
- Phương pháp tính tích phân hàm ẩn cực hay
- Lý thuyết ứng dụng tích phân trong hình học cực hay
- Giải nhanh tích phân bằng casio cực hay





