Giải SGK bài Đại lượng tỉ lệ nghịch Toán 7 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Đại lượng tỉ lệ nghịch. Các bài tập sau đây thuộc bài 3 chương 6 – Các đại lượng tỉ lệ trang 16, 17, 18, 19, 20 Toán 7 Chân trời sáng tạo tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Đại lượng tỉ lệ nghịch
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 16, 17, 18, 19 trong bài Đại lượng tỉ lệ nghịch. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 16
Em hãy tính tích s.m và tìm s khi:
m = 0,5
m = 1
m = 2
b) Một vòi nước chảy vào bể cạn có dung tích là 100 l. Gọi V là số lít nước chảy được từ vòi vào bể trong một giờ và gọi t là thời gian để vòi chảy đầy bể.
Em hãy lập công thức tính t theo V và tìm t khi:
V = 50
V = 100
V = 200
Lấy tổng số đậu xanh chia cho khối lượng mỗi gói để tìm ra số gói
Lấy dung tích của bể chia cho lượng nước bơm vào mỗi giờ để tính thời gian
a) Khi m = 0,5 ta có s = 20 : 0,5 = 40
Vậy khi m = 0,5 thì s = 40
Khi m = 1 ta có s = 20 : 1 = 20
Vậy khi m = 1 thì s = 20
Khi m = 2 ta có s = 20 : 2 = 10
Vậy khi m = 2 thì s = 10
b) Ta có: V . t = 100 nên t = 100 : V
Khi V = 50 ta có t = 100 : 50 = 2
Khi V = 100 ta có t = 100 : 50 = 1
Khi V = 200 ta có t = 100 : 200 = 0,5
Thực hành trang 17
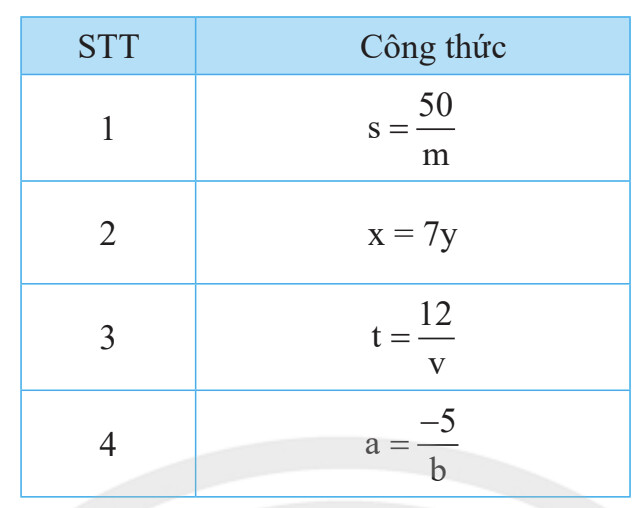
Nếu hai đại lượng y và x liên hệ với nhau bởi công thức
$y=\frac{a}{x}$ hay $x y=a$ ( với a là hằng số) thì $y$ và $x$ là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a.
Xét công thức : $s=\frac{50}{m}$ ta thấy s tỉ lệ nghịch với $\mathrm{m}$ theo hệ số tỉ lệ 50
Xét công thức : x = 7y ta thấy y tỉ lệ thuận với $x$ theo hệ số tỉ lệ 7
Xét công thức : $t=\frac{12}{v}$ ta thấy $t$ tỉ lệ nghịch với v theo hệ số tỉ lệ là 12
Xét công thức : $a=\frac{-5}{b}$ ta thấy a tỉ lệ nghịch với b theo hệ số tỉ lệ -5
Vận dụng 1 trang 17
Chiều dài . Chiều rộng = Diện tích hình chữ nhật
Vì a và b là chiều dài và chiều rộng của hình chữ nhật nên diện tích = a.b =12
⇒ b tỉ lệ nghịch với a theo hệ số tỉ lệ là 12.
Hoạt động 2 trang 17

a) Tìm hệ số tỉ lệ
b) Tìm mỗi giá trị thích hợp cho mỗi dấu ? trong bảng trên
c) Em có nhận xét gì về tích hai giá trị tương ứng $x_1 y_1 ; x_2 y_2 ; x_3 y_3 ; x_4 y_4 ; x_5 y_5$ của x và y
a) Xét $x_1 ; y_1$ vì y tỉ lệ nghịch với x nên ta có công thức :
$x_1 \cdot y_1=1.10=10 \Rightarrow \text { Hệ số tỉ lệ }=10$
b) Vì x.y $=10$ nên ta có :
$ \Rightarrow x_2 . y_2=2.?=10 \Rightarrow ?=5 $
$ \Rightarrow x_3 . y_3=3. ?=10 \Rightarrow ?=\frac{10}{3} $
$ \Rightarrow x_4 . y_4=4 . ?=10 \Rightarrow ?=2,5 $
$ \Rightarrow x_5 y_5=5 . ?=10 \Rightarrow ?=2$
c) Ta thấy tích hai giá trị tương ứng $x_1 y_1 ; x_2 y_2 ; x_3 y_3 ; x_4 y_4 ; x_5 y_5$ không đổi ( luôn bằng 10).
Vận dụng 2 trang 18
Tìm số lần tăng lên của số từ mỗi phút đọc được
Từ đó tìm tỉ lệ thời gian đọc mới và cũ
Vì số trang đọc được 1 phút tăng gấp đôi nên thời gian đọc mới = $\frac{1}{2}$ thời gian đọc cũ.
Ta có tỉ số giữa thời gian đọc xong cùng một quyển sách theo phương pháp mới và cũ của bạn Quỳnh là: $\frac{1}{2}$.
Vận dụng 3 trang 19
Một người đi xe đạp từ A đến B với vận tốc không đổi là 20 km/h mất 6 giờ. Hỏi nếu người đó đi bằng xe gắn máy với vận tốc không đổi là 40 km/h thì mất bao nhiêu thời gian.
Tính độ dài quãng đường AB
Từ độ dài AB vừa tính được ta tính thời gian dựa vào vận tốc
Chú ý: Quãng đường = vận tốc . thời gian
Độ dài quãng đường AB là : 20.6 = 120km
Người đó đi với vận tốc 40km trên quãng đường AB mất:
120 : 40 = 3 giờ
Giải bài tập SGK bài Đại lượng tỉ lệ nghịch
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Đại lượng tỉ lệ thuận trang 20 sách Toán 7 chân trời sáng tạo tập 2 dưới đây nhé!
Bài tập 1 trang 20
a) Tìm hệ số tỉ lệ
b) Hãy biểu diễn a theo b
c) Tính giá trị của a khi b = 2, b = 14
Hai đại lượng a và b tỉ lệ nghịch theo hệ số k nếu a.b = k ( k là hằng số)
a) Vì a tỉ lệ nghịch với b và $a=3, b=-10$
Áp dụng công thức tỉ lệ nghịch ta có :
$a . b=3 .(-10)=-30$
Vậy hệ số tỉ lệ là -30
b) Ta có $a .b=-30$
$\Rightarrow a=\frac{-30}{b}$
c) Theo công thức $a=\frac{-30}{b}$
Khi $b=2$ thì $a=\frac{-30}{2}=-15$
Khi $b=14$ thì $a=\frac{-30}{14}=\frac{-15}{7}$
Bài tập 2 trang 20

a) Tìm hệ số tỉ lệ
b) Tìm các giá trị chưa biết trong bảng trên
a) Nếu đại lượng x và y liên hệ với nhau bởi công thức x.y = a không đổi thì x, y là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ a.
b) Thay giá trị x ( hoặc y) đã biết vào công thức ở câu a để tính giá trị y ( hoặc x) tương ứng.
a) Khi $x=-8$ thì $y=-5$
Theo công thức tỉ lệ nghịch ta có : x.y $=(-5) .(-8)=40$
Vậy hệ số tỉ lệ là 40
b) Khi $x=5$ ta có : $5 . y=40 \Rightarrow y=8$
Khi $x=4$ ta có : $4 . y=40 \Rightarrow y=10$
Khi $\mathrm{y}=9$ ta có $: 9 . \mathrm{x}=40 \Rightarrow x=\frac{40}{9}$
Khi $x=6$ ta có $: 6 . y=40 \Rightarrow y=\frac{40}{6}=\frac{20}{3}$
Khi $x=12$ ta có $12. y=40 \Rightarrow y=\frac{40}{12}=\frac{10}{3}$
Bài tập 3 trang 20
Số công nhân và số ngày hoàn thành là hai đại lượng tỉ lệ nghịch.
Gọi thời gian mà 12 người cần để đóng xong chiếc tàu là $x$(ngày)$(x>0)$
Vì số công nhân tỉ lệ nghịch với số ngày hoàn thành nên theo tính chất 2 đại lượng tỉ lệ nghịch, ta được:
$20.60=12 . x $
$\Rightarrow x=\frac{20.60}{12}=100$
Vậy nếu chỉ còn 12 công nhân thì họ đóng xong chiếc tàu đó trong 100 ngày.
Bài tập 4 trang 20
Sử dụng định nghĩa về tỉ lệ nghịch
Hai đại lượng x và y có tỉ lệ nghịch với nhau vì tích x.y luôn không đổi
Bài tập 5 trang 20
Nếu hai đại lượng x và y liên hệ với nhau bởi công thức x.y = a không đổi thì x và y là hai đại lượng tỉ lệ nghịch với nhau
Chu vi bánh xe . số vòng quay được của bánh xe = Quãng đường xe đi từ A đến B ( không đổi) nên ta được:
$a . b = s$ ( s không đổi).
Do đó, a và b là hai đại lượng tỉ lệ nghịch với nhau.
Bài tập 6 trang 20

Xét các tích a.b tương ứng:
+) Nếu các tích này đều bằng nhau thì a và b là hai đại lượng tỉ lệ nghịch.
+) Nếu các tích này khác nhau thì a và b không là hai đại lượng tỉ lệ nghịch.
a) Xét a.b ta có :
$a.b = 1.60 = 2.30 = 3.20 = 4.15 = 5.12$ vì cùng bằng $60$
Vậy a tỉ lệ nghịch với b
b) Xét $ m.n$ ta có :
$m.n = (-2).(-12) = (-1).(-24) = 1.24 = 2.12 ≠ 3.9$
Ta thấy khi $m = 3$ và $n = 9$ thì hệ số tỉ lệ là khác với các giá trị còn lại nên m không tỉ lệ nghịch với n.
Bài tập 7 trang 20
Sô máy gặt và thời gian là hai đại lượng tỉ lệ nghịch
Vì khối lượng công việc không đổi và các máy có cùng năng suất nên số máy gặt tỉ lệ nghịch với thời gian.
Ta có: Số máy gặt . thời gian = 2.4 = 8
Nếu có 4 máy gặt thì thời gian gặt = 8 : 4 = 2 (giờ)
Vậy nếu có 4 máy gặt như thế sẽ gặt xong cánh đồng đó hết 2 giờ.
Bài tập 8 trang 20
Nếu hai đại lượng a và b liên hệ với nhau theo công thức a . b = k không đổi thì a và b là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ k.
Vì diện tích hình chữ nhật bằng tích chiều dài và chiều rộng nên ta có : $n.d = 24 $
⇒ n tỉ lệ nghịch với d có hệ số tỉ lệ là 24
⇒$n=\frac{24}{d}$
Bài tập 9 trang 20
Thời gian(h) . vận tốc(km/h) = quãng đường (km)
Công thức tính quãng đường là : $S = v.t$
Theo đề bài $S = 200km$ nên ta có$ 200 = v.t$
Vì $v.t = 200$ không đổi nên v tỉ lệ nghịch với t theo hệ số tỉ lệ là 200.
⇒ $t=\frac{200}{v}$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 3 chương 6 – Các đại lượng tỉ lệ trang 16, 17, 18, 19, 20 Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




