Giải SGK bài 3 chương 7 trang 33, 34, 35, 36 Toán 7 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Phép cộng và phép trừ đa thức một biến. Các bài tập sau đây thuộc bài 3 chương 7 – Biểu thức đại số trang 33, 34, 35, 36 Toán 7 Chân trời sáng tạo tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Phép cộng và phép trừ đa thức một biến
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 33, 34, 35 trong bài Phép cộng và phép trừ đa thức một biến. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 33
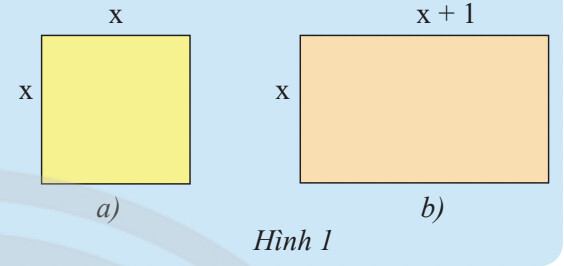
Chu vi hình vuông là: 4. Cạnh
Chu vi hình chữ nhật là: 2.(chiều dài + chiều rộng)
Chu vi của hình vuông là: $4x$.
Chu vi của hình chữ nhật là: $2 . (x + x + 1) = 2 . (2x + 1) = 2 . 2x + 2 . 1 = 4x + 2$.
Tổng chu vi của hình vuông và hình chữ nhật là: $4x + 4x + 2 = 8x + 2$.
Thực hành 1 trang 34
Hãy tính $\mathrm{P}(\mathrm{x})+$ $\mathrm{Q}(\mathrm{x})$ bằng hai cách.
Cách 1: Nhóm các đơn thức cùng lũy thừa rồi thực hiện phép cộng
Cách 2: Sắp xếp đa thức theo bậc giảm dần rồi đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Cách 1:
$ \mathrm{P}(\mathrm{x})+\mathrm{Q}(\mathrm{x})=7 x^3-8 x+12+6 x^2-2 x^3+3 x-5 $
$ =\left(7 x^3-2 x^3\right)+6 x^2+(-8 x+3 x)+(12-5) $
$ =5 x^3+6 x^2-5 x+7$
Cách 2:
$Q(x)=6 x^2-2 x^3+3 x-5=-2 x^3+6 x^2+3 x-5$
Khi đó thực hiện đặt phép tính ta có:
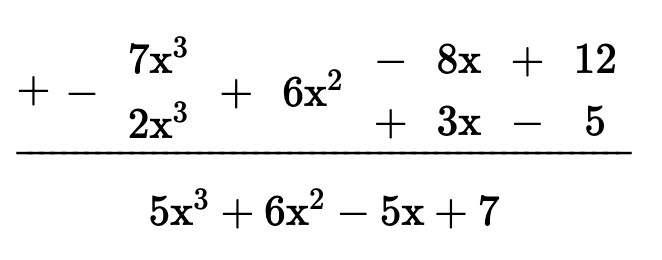
Vậy $P(x)+Q(x)=5 x^3+6 x^2-5 x+7$
Hoạt động 2 trang 34
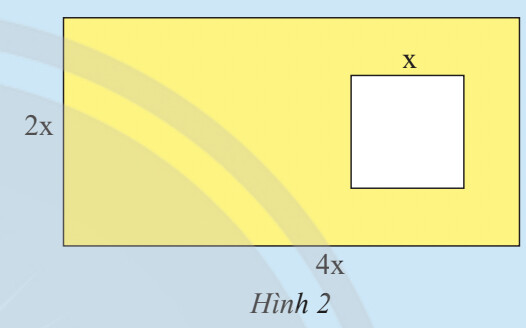
Tính diện tích hình chữ nhật lớn
Tính diện tích hình vuông
Tính diện tích phần màu vàng cần tìm
Biểu thức biểu thị diện tích của hình chữ nhật là: $4x . 2x = 8x^2$.
Biểu thức biểu thị diện tích của hình vuông là: $x^2$.
Biểu thức biểu thị diện tích phần được tô vàng trong Hình 2 là: $8x^2 – x^2 = 7x^2$.
Thực hành 2 trang 35
Hãy tính P(x) – Q(x) bằng hai cách.
Cách 1: Nhóm các đơn thức cùng lũy thừa rồi thực hiện phép trừ
Cách 2: Sắp xếp đa thức theo bậc giảm dần rồi đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.
Cách 1 :
Ta có P(x) – Q(x)
$= 2x^3 – 9x^2 + 5 – (2x^2 + 4x^3 – 7x)$
$= 2x^3 – 9x^2 + 5 – 2x^2 – 4x^3 + 7x$
$= (2x^3 – 4x^3) + (-9x^2 – 2x^2) + 7x + 5$
$= -2x^3 – 11x^2 + 7x + 5$
Cách 2:
$Q(x) = -2x^2 – 4x^3 + 7x = – 4x^3 – 2x^2 + 7x$
Khi đó thực hiện đặt phép tính ta có:
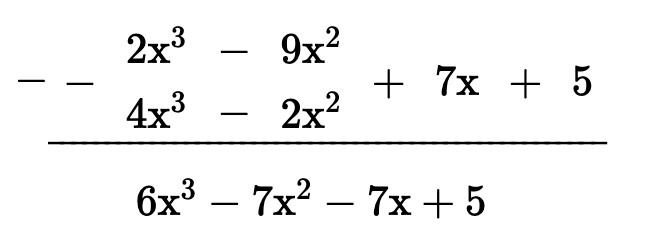
Vậy $P(x) – Q(x) = 6x^3 – 7x^2 – 7x + 5$.
Thực hành 3 trang 35
Bỏ dấu ngoặc rồi nhóm các đơn thức cùng lũy thừa.
$(x – 4) + [(x^2 + 2x) + (7 – x)]$
$= x – 4 + x^2 + 2x + 7 – x$
$= x^2 + (x + 2x – x) + (-4 + 7)$
$= x^2 + 2x + 3$
Giải bài tập SGK bài Phép cộng và phép trừ đa thức một biến
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Phép cộng và phép trừ đa thức một biến trang 35, 36 sách Toán 7 chân trời sáng tạo tập 2 dưới đây nhé!
Bài tập 1 trang 35
Hãy tính P(x) + Q(x) và P(x) – Q(x).
Tính P(x) + Q(x):
P(x) + Q(x) = $(-3x^4 – 8x^2 + 2x) + (5x^3 – 3x^2 + 4x – 6)$
P(x) + Q(x) = $-3x^4 – 8x^2 + 2x + 5x^3 – 3x^2 + 4x – 6$
P(x) + Q(x) = $-3x^4 + 5x^3 + (-8x^2 – 3x^2) + (2x + 4x) – 6$
P(x) + Q(x) = $-3x^4 + 5x^3 – 11x^2 + 6x – 6$
Tính P(x) – Q(x):
P(x) – Q(x) = $(-3x^4 – 8x^2 + 2x) – (5x^3 – 3x^2 + 4x – 6)$
P(x) – Q(x) = $-3x^4 – 8x^2 + 2x – 5x^3 + 3x^2 – 4x + 6$
P(x) – Q(x) = $-3x^4 – 5x^3 + (-8x^2 + 3x^2) + (2x – 4x) + 6$
P(x) – Q(x) = $-3x^4 – 5x^3 – 5x^2 – 2x + 6$
Vậy P(x) + Q(x) = $-3x^4 + 5x^3 – 11x^2 + 6x – 6$; P(x) – Q(x) = $-3x^4 – 5x^3 – 5x^2 – 2x + 6$.
Bài tập 2 trang 35
Tìm đa thức N(x) sao cho M(x) + N(x) =$ 3x^2 – 2x$.
M(x) + N(x) = P(x) thì N(x) = P(x) – M(x)
Do $M(x) + N(x) = 3x^2 – 2x$ nên $N(x) = 3x^2 – 2x – M(x)$
N(x) = $3x^2 – 2x – (7x^3 – 2x^2 + 8x + 4)$
N(x) = $3x^2 – 2x – 7x^3 + 2x^2 – 8x – 4$
N(x) =$ -7x^3 + (3x^2 + 2x^2) + (-2x – 8x) – 4$
N(x) =$ -7x^3 + 5x^2 – 10x – 4$
Vậy N(x) =$ -7x^3 + 5x^2 – 10x – 4$.
Bài tập 3 trang 36
Tìm đa thức B(y) sao cho B(y) – A(y) = $2y^3 – 9y^2 + 4y$.
B(y) = B(y) – A(y) + A(y)
Do $B(y) – A(y) = 2y^3 – 9y^2 + 4y$ nên $B(y) = A(y) + 2y^3 – 9y^2 + 4y$
B(y) = $(-5y^4 – 4y^2 + 2y + 7) + 2y^3 – 9y^2 + 4y$
B(y) =$ -5y^4 – 4y^2 + 2y + 7 + 2y^3 – 9y^2 + 4y
B(y) = $-5y^4 + 2y^3 + (-4y^2 – 9y^2) + (2y + 4y) + 7$
B(y) =$ -5y^4 + 2y^3 -13y^2 + 6y + 7$
Vậy B(y) = $-5y^4 + 2y^3 -13y^2 + 6y + 7$
Bài tập 4 trang 36
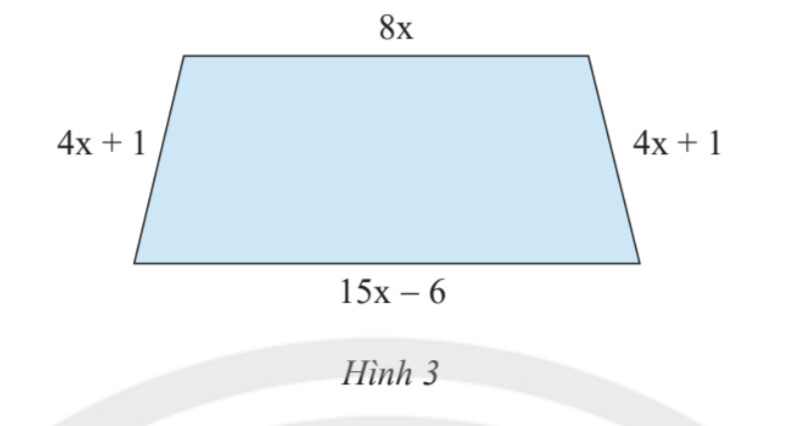
Biểu thức biểu thị chu vi của hình thang cân là:
$8x + 4x + 1 + 15x – 6 + 4x + 1$
$= (8x + 4x + 15x + 4x) + (1 – 6 + 1)$
$= 31x – 4$
Vậy biểu thức biểu thị chu vi của hình thang cân là $31x – 4$.
Bài tập 5 trang 36
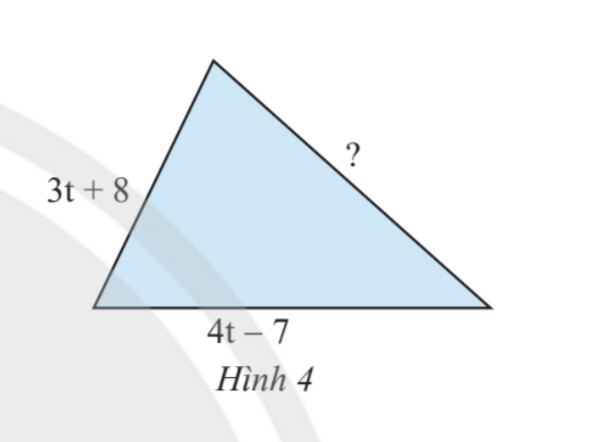
Cạnh tam giác = chu vi – tổng độ dài 2 cạnh còn lại.
Độ dài cạnh còn lại của tam giác bằng:
$12t – 3 – (3t + 8) – (4t – 7)$
$= 12t – 3 – 3t – 8 – 4t + 7$
$= (12t – 3t – 4t) + (-3 – 8 + 7)$
$= 5t – 4$
Bài tập 6 trang 36
R(x) = $-2x^4 + 4x^2 + 2x – 10$.
Tính P(x) + Q(x) + R(x) và P(x) – Q(x) – R(x).
+ Bước 1: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc.
+ Bước 2: Nhóm các đơn thức cùng lũy thừa của biến
+ Bước 3: Thu gọn
P(x) + Q(x) + R(x)=$9 x^4-3 x^3+5 x-1-2 x^3-5 x^2+3 x-8-2 x^4+4 x^2+2 x-10 $
$ =(9 x^4-2 x^4)+(-3 x^3-2 x^3)+(-5 x^2+4 x^2)+(5 x+3 x+2 x)+(-8-10-1)$
$ =7 x^4-5 x^3-x^2+10 x-19$
P(x) – Q(x) – R(x)=$9 x^4-3 x^3+5 x-1+2 x^3+5 x^2-3 x+8+2 x^4-4 x^2-2 x+10 $
$=(9 x^4+2 x^4)+(-3 x^3+2 x^3)+(5 x^2-4 x^2)+(5 x-3 x-2 x)+(10-1+8)$
$ =11 x^4-x^3+x^2+17$
Bài tập 7 trang 36
Ta thấy trong đa thức P(x) chưa có hạng tử thức bậc 4 nên ta sẽ thêm đơn thức bậc 4 vào đa thức sao cho kết quả của đa thức là không đổi.
Đặt A(x) = $x^4 + x^3 – 4x^2$
Khi đó P(x) = A(x) + B(x).
Suy ra B(x) = P(x) – A(x)
B(x) = $(x^3 – 4x^2 + 8x – 2) – (x^4 + x^3 – 4x^2)$
B(x) = $x^3 – 4x^2 + 8x – 2 – x^4 – x^3 + 4x^2$
B(x) = $-x^4 + (x^3 – x^3) + (-4x^2 + 4x^2) + 8x – 2$
B(x) = $-x^4 + 8x – 2$
Vậy P(x) = $(x^4 + x3 – 4x^2) + (-x^4 + 8x – 2)$.
Bài tập 8 trang 36
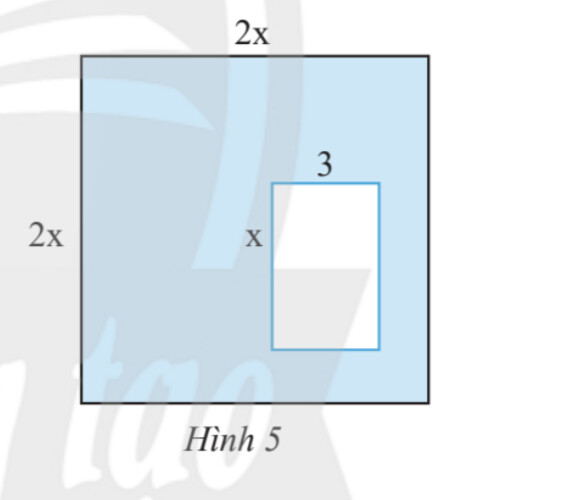
Ta tính diện tích hình vuông lớn
Tính diện tích hình chữ nhật nhỏ
Lấy diện tích hình vuông trừ đi diện tích hình chữ nhật để ra được phần cần tìm
Biểu thức biểu thị diện tích hình vuông là: $2x . 2x = 4x^2$
Biểu thức biểu thị diện tích hình chữ nhật là: $3x$
Biểu thức biểu thị diện tích của phần được tô màu xanh là: $4x^2 – 3x$
Bài tập 9 trang 36
b) Cho A = $4x + 2, C = 5 – 3x^2$. Tìm đa thức B sao cho A + B = C.
a) Bước 1: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc.
+Bước 2: Nhóm các đơn thức cùng lũy thừa
+ Bước 3: Thu gọn
b) Ta tính C – A = B
a)
$ (3 x-1)+[(2 x^2+5 x)+(4-3 x)]=3 x-1+2 x^2+5 x+4-3 x$
$ =2 x^2+(3 x+5 x-3 x)+(4-1)=2 x^2+5 x+3$
b)
Vì $A+B=C$ nên $B=C-A$
Ta được: $B=5-3 x^2-4 x-2$
$=-3 x^2-4 x+3$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Phép cộng và phép trừ đa thức một biến thuộc chương 7 – Biểu thức đại số trang 33, 34, 35, 36 Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




