Giải SGK bài 2 chương 2 trang 35, 36, 37, 38 Toán 7 Chân trời sáng tạo tập 1
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Số thực. Giá trị tuyệt đối của một số thực. Đây là bài học thuộc bài 2 chương 2 trang 35, 36, 37, 38 sách Toán 7 Chân trời sáng tạo tập 1. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK bài Số thực. Giá trị tuyệt đối của một số thực
Dưới đây là phương pháp và bài giải chi tiết cho hoạt động khởi động, hoạt động khám phá, vận dụng cùng phần thực hành ở các trang 35, 36, 37 trong bài Số thực. Giá trị tuyệt đối của một số thực. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động khởi động trang 35
Người ta sẽ gọi tập gồm các số hữu tỉ và các số vô tỉ là tập số thực.
Hoạt động khám phá 1 trang 35
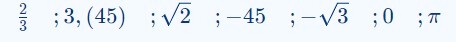
– Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.
– Số hữu tỉ được viết dưới dạng $\frac{a}{b}$, trong đó a và b là các số nguyên, b khác 0 .
Ta có: $3,(45)=\frac{38}{11} ;-45=\frac{-45}{1} ; 0=\frac{0}{1}$ do đó:
Các số hữu tỉ là: $\frac{2}{3} ; 3,(45) ;-45 ; 0$.
Các số vô tỉ là: $\sqrt{2} ;-\sqrt{3} ; \pi$.
Chú ý: Số thập phân vô hạn tuần hoàn cũng là số hữu tỉ.
Thực hành 1 trang 35
a) $\sqrt{3} \in \mathbb{Q}$
b) $\sqrt{3} \in \mathbb{R}$
c) $\frac{2}{3} \notin \mathbb{R}$
d) $-9 \in \mathbb{R}$
Số hữu tỉ được viết dưới dạng $\frac{a}{b}$, trong đó a và b là các số nguyên, b khác 0 . Kí hiệu là $\mathbb{Q}$.
– Số thực bao gồm cả số vô tỉ và số hữu tỉ. Kí hiệu là $\mathbb{R}$.
a) $\quad \sqrt{3} \in \mathbb{Q}$ sai.
Sửa lại: $\sqrt{3} \notin \mathbb{Q}$
b) $\sqrt{3} \in \mathbb{R}$ đúng.
C) $\quad \frac{2}{3} \notin \mathbb{R}$ sai.
Sửa lại: $\frac{2}{3} \in \mathbb{R}$
d) $\quad-9 \in \mathbb{R}$ đúng.
Hoạt động khám phá 2 trang 35
Để so sánh các số thập phân ta so sánh lần lượt các hàng từ trái qua phải với nhau.
Ta có:
$3,14 \lt 3,141515 \lt 3,141515(15)$
Vậy $3,14 \lt 3,141515 \lt 3,14(15)$
Thực hành 2 trang 36
a) $4,(56)$ và $4,56279$ ;
b) $-3,(65)$ và $-3,6491$;
c) $0,(21)$ và $0,2(12)$;
d) $\sqrt{2}$ và $1,42$.
Ta có thể so sánh hai số thực bằng cách so sánh hai số thập phân (hữu hạn hoặc vô hạn) biểu diễn chúng
a) Ta có: $4,(56)=4,5656 \ldots$
Vì $4,5656 … \gt 4,56279$ nên $4,(56) \gt 4,56279$
b) Ta có:
$-3,(65)=-3,6565 \ldots$
Vì $3,6565… \gt 3,6491$ nên $-3,6565 \ldots \lt -3,6491$.
Do đó, $-3,(65) \lt -3,6491$;
c) $0,(21)=\frac{7}{33}$ và $0,2(12)=\frac{7}{33}$
Nên $0,(21)=0,2(12)$.
d) $\sqrt{2}=1,41421 \ldots \lt 1,42$
Vận dụng 1 trang 36
Tính cạnh hình vuông: $a=\sqrt{S}$
– So sánh $a$ và $b$.
Cạnh hình vuông là: $a=\sqrt{5}=2,236 \ldots(\mathrm{m})$
Ta có: $2,236 \ldots \lt 2,361$ nên $a \lt b$.
Hoạt động khám phá 3 trang 36
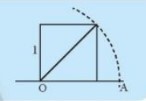
$OA$ là đường chéo của hình vuông có cạnh là $1$ => Độ dài đường chéo.
Đường chéo của hình vuông có độ dài đường chéo là $1$ bằng $\sqrt{2}$.
$\sqrt{2}$ là số vô tỉ.
Thực hành 3 trang 36
Mỗi điểm trên trục số biểu diễn một số thực.
Vẽ trục số, các số thực âm nằm bên trái số 0, các số thực dương nằm bên phải số 0 .

Vận dụng 2 trang 36
Trên trục số, số nhỏ hơn sẽ nằm bên trái số lớn hơn
Do $\sqrt{2}=1,41 \ldots<\frac{3}{2}=1,5$ nên số $\sqrt{2}$ nằm bên trái số $\frac{3}{2}$.
Hoạt động khám phá 4 trang 37

Gọi $A$ và $A’$ lần lượt là hai điểm biểu diễn hai số $4,5$ và $-4,5$ trên trục số. So sánh $OA$ và $OA’$.
Quan sát hình vẽ để tính $OA$ và $OA’$ sau đó so sánh.
Ta có: $OA = 4,5$ và $OA’=4,5$ nên $OA=OA’$.
Thực hành 4 trang 37
Số đối của số thực $x$ kí hiệu là $-x$
Số đối của số: $5,12$ là $-5,12$
Số đối của số: $\pi$ là $-\pi$
Số đối của số: $-\sqrt{13}$ là $\sqrt{13}$.
Chú ý:
Muốn tìm số đối của một số ta chỉ cần đổi dấu của nó.
Vận dụng 3 trang 37
Tìm số đối của hai số trên.
So sánh hai số đối vừa tìm được.
Số đối của hai số $\sqrt{2}$ và $\sqrt{3}$ lần lượt là $-\sqrt{2}$ và $-\sqrt{3}$
Do $2<3 \Rightarrow \sqrt{2}-\sqrt{3}$.
Chú ý:
Với hai số thực a,b dương. Nếu $\mathrm{a}>\mathrm{b}$ thì $\sqrt{a}>\sqrt{b}$.
Hoạt động khám phá 5 trang 37
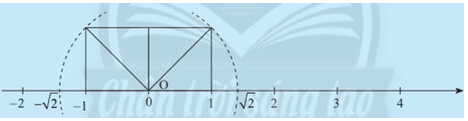
Quan sát hình vẽ và so sánh khoảng cách từ 0 đến hai điểm $\sqrt{2}$ và $-\sqrt{2}$.
Ta thấy khoảng cách từ 0 đến điểm $\sqrt{2}$ bằng $\sqrt{2}$.
Khoảng cách từ 0 đến điểm $-\sqrt{2}$ bằng $\sqrt{2}$
Vậy khoảng cách từ 0 đến hai điểm $\sqrt{2}$ và $-\sqrt{2}$ bằng nhau.
Thực hành 5 trang 37
$$\begin{aligned}& |x|=x \text { nếu } x>0 \\& |x|=-x \text { nếu } x<0 \\& |x|=0 \text { nếu } x=0\end{aligned}$$
|-3,14|=3,14 \\\\ |41|=41 \\\\ |-5|=5 \\\\ |1,(2)|=1,(2) \\\\ |-\sqrt{5}|=\sqrt{5}
Vận dụng 4 trang 37
Giá trị tuyệt đối của một số thực âm hoặc dương đều là một số hữu tỉ dương.
Có hai số thực $x$ thỏa mãn là: $x=\sqrt{3} ; x=-\sqrt{3}$.
Giải bài tập SGK bài Số thực. Giá trị tuyệt đối của một số thực
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 38 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Số thực. Giá trị tuyệt đối của một số thực ở trên.
Bài 1 trang 38
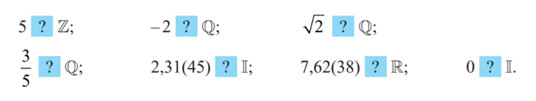
$$\begin{aligned}& \mathbb{Z}=\{\ldots ;-2 ;-1 ; 0 ; 1 ; 2 ; \ldots\} \\& \mathbb{Q}=\left\{\frac{a}{b} \mid a, b \in \mathbb{Z} ; b \neq 0\right\}\end{aligned}$$
Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ. Kí hiệu là II. Tập hợp số hữu tỉ $\mathbb{R}$ bao gồm các số vô tỉ và hữu tỉ.

Bài 2 trang 38
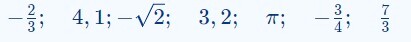
Viết các số thực dưới dạng số thập phân rồi so sánh và sắp xếp theo thứ tự từ nhỏ đến lớn.
Ta có:
-\frac{2}{3}=-0,(6) ; \quad 4,1 ;\quad -\sqrt{2}=-1,414 \ldots ; \quad 3,2 \\\\ \pi=3,141 \ldots ; \quad-\frac{3}{4}=-0,75 ; \quad \frac{7}{3}=2,(3)
Do -1,414 \ldots \lt -0,75 \lt -0,(6) \lt 2,(3) \lt 3,141 \ldots \lt 3,2 \lt 4,1 \\\\ \text { Nên }-\sqrt{2} \lt -\frac{3}{4} \lt -\frac{2}{3} \lt \frac{7}{3} \lt \pi \lt 3,2 \lt 4,1 \text {. }
Bài 3 trang 38
a) $\sqrt{2} ; \sqrt{3} ; \sqrt{5}$ là các số thực.
b) Số nguyên không là số thực.
c) $-\frac{1}{2} ; \frac{2}{3} ;-0,45$ là các số thực.
d) Số $0$ vừa là số hữu tỉ vừa là số vô tỉ.
e) $1; 2; 3; 4$ là các số thực.
Tập hợp số hữu tỉ $\mathbb{R}$ bao gồm các số vô tỉ và hữu tỉ.
a) $\sqrt{2} ; \sqrt{3} ; \sqrt{5}$ là các số thực => Đúng
b) Số nguyên không là số thực => Sai (Do Tất cả các số nguyên đều là số thực)
c) $-\frac{1}{2} ; \frac{2}{3} ;-0,45$ là các số thực => Đúng
d) Số $0$ vừa là số hữu tỉ vừa là số vô tỉ => Sai (Do số 0 không là số vô tỉ)
e) $1; 2; 3; 4$ là các số thực => Đúng.
Chú ý: Số thực là tập hợp số lớn nhất, bao gồm tất cả các tập hợp số đã được học.
Bài 4 trang 38

Sử dụng quy tắc so sánh hai số thập phân rồi điền số vào dấu “?”
a) $2,71467 \gt 2,70932$
b) $5,17934 \lt 5,17946$ nên $-5,17934 \gt -5,17946$
Bài 5 trang 38
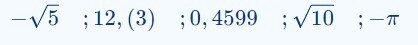
Số đối của số $x$ kí hiệu là $-x$.
Muốn tìm số đối của một số thực bất kì ta chỉ việc đổi dấu của chúng.
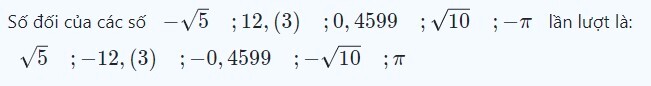
Bài 6 trang 38
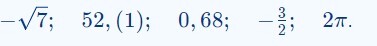
$|x|=x$ nếu $x>0$
$|x|=-x$ nếu $x<0$
$|x|=0$ nếu $x=0$.
$$|-\sqrt{7}|=\sqrt{7} ; \quad|52,(1)|=52,(1) ; \quad|0,68|=0,68 ; \quad\left|-\frac{3}{2}\right|=\frac{3}{2} ; \quad|2 \pi|=2 \pi .$$
Bài 7 trang 38
$$-3,2 ; 2,13 ;-\sqrt{2} ;-\frac{3}{7} \text {. }$$
– Tính giá trị tuyệt đối của các số trên
– So sánh rồi sắp xếp theo thứ tự từ nhỏ đến lớn.
Chú ý: Cách tính giá trị tuyệt đối
$$\begin{aligned}& |x|=x \text { nếu } x>0 \\& |x|=-x \text { nếu } x<0 \\& |x|=0 \text { nếu } x=0\end{aligned}$$
$|-3,2|=3,2 ; \\\\ |2,13|=2,13 ; \\\\ |-\sqrt{2}|=\sqrt{2}=1,41 . . ; \\\\ |-\frac{3}{7}|=\frac{3}{7}=0,42 \ldots$
Do $0,42 \lt 1,41 \ldots \lt 2,13<3,2 $ nên:
|-\frac{3}{7}| \lt |-\sqrt{2}| \lt |2,13| \lt |-3,2| .
Bài 8 trang 38
Tìm $\mathrm{x}$, biết: $|x|=a$
TH1: $a>0$ thì $x=a$ hoặc $x=-a$.
TH2: $a=0$ thì $x=0$.
TH3: $a<0$ thì không có giá trị nào của $x$ thỏa mãn.
\text { +) }|x|=\sqrt{5} \Rightarrow x=\sqrt{5} \text { hoặc } x=-\sqrt{5} \\\\ \text { +) }|y-2|=0 \Rightarrow y-2=0 \Rightarrow y=2 \\\\ \text { Vậy } x \in\{\sqrt{5} ;-\sqrt{5}\} ; y=2
Bài 9 trang 38
– Tính trị tuyệt đối sau đó tính căn bặc hai.
– Cách tính giá trị tuyệt đối:
$|x|=x$ nếu $x>0$
$|x|=-x$ nếu $x<0$
$|x|=0$ nếu $x=0$
Do $|-9|=9$ nên ta có:
$$M=\sqrt{|-9|}=\sqrt{9}=3$$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Số thực. Giá trị tuyệt đối của một số thực Chương Số thực Toán 7 Chân trời sáng tạo tập 1 ở các trang 35, 36, 37, 38. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!




