Giải SGK bài Các góc ở vị trí đặc biệt trang chương 4 Toán 7 Chân trời sáng tạo tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Các góc ở vị trí đặc biệt. Các bài tập sau đây thuộc bài 1 chương 4 – Góc và đường thẳng song song trang 69, 70, 71, 72 Toán 7 Chân trời sáng tạo tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Các góc ở vị trí đặc biệt
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 69, 70, 71 trong bài Các góc ở vị trí đặc biệt. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 69
– Cạnh nào chung?
– Điểm trong nào chung?
b) Hãy đo các góc $\widehat{x O y}, \widehat{y O z}, \widehat{x O z}$ trong Hình 1 rồi so sánh tổng số đo của $\widehat{x O y}$ và $\widehat{y O z}$ với $\widehat{x O z}$.
c) Tính tổng số đo của hai góc $\widehat{m O n}$ và $\widehat{n O p}$ trong Hình 2.
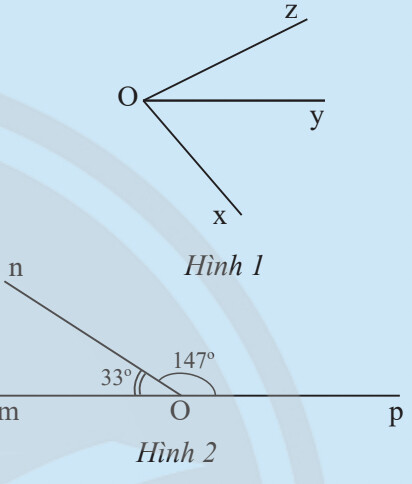
Quan sát, đo và tính.
a) Hai góc $\widehat{x O y}$ và $\widehat{y O z}$ có cạnh Oy chung, không có điểm trong chung
b) Ta có:
$ \widehat{x O y}=30^{\circ}, \widehat{y O z}=45^{\circ}, \widehat{x O z}=75^{\circ} $
$ \Rightarrow \widehat{x O y}+\widehat{y O z}=\widehat{x O z}$
c) Ta có: $\widehat{m O n}+\widehat{n O p}=33^{\circ}+147^{\circ}=180^{\circ}$
Thực hành 1 trang 69
a) Tìm các góc kề với $\widehat{\mathrm{OZz}}$.
b) Tìm số đo của góc kề bù với $\widehat{\mathrm{mOn}}$.
c) Tìm số đo của $\widehat{\mathrm{nOy}}$.
d) Tìm số đo của góc kề bủ với tOz.
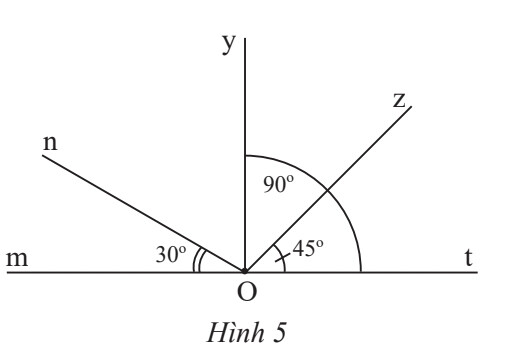
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ
a) Các góc kề với $\widehat{t O z}$ là: $\widehat{z O y}, \widehat{z O n}, \widehat{z O m}$
b) Ta có: $\widehat{m O n}=30^{\circ}$ nên góc kề bù với $\widehat{m O n}$ có số đo là: $180^{\circ}-30^{\circ}=150^{\circ}$
c) Ta có:
$ \widehat{m O n}+\widehat{n O y}+\widehat{y O t}=180^{\circ} $
$ \Rightarrow 30^{\circ}+\widehat{n O y}+90^{\circ}=180^{\circ} $
$ \Rightarrow \widehat{n O y}=180^{\circ}-30^{\circ}-90^{\circ}=60^{\circ}$
Vậy $ \widehat{n O y}=60^{\circ}$
d) Ta có: $\widehat{t O z}=45^{\circ}$ nên góc kề bù với $\widehat{t O z}$ có số đo là: $180^{\circ}-45^{\circ}=135^{\circ}$
Vận dụng 1 trang 70
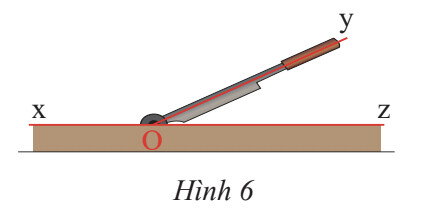
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ
2 góc vừa kề vừa bù nhau thì là hai góc kề bù
Hai góc kề bù trong hình trên là: $\widehat{xOy}$ và $\widehat{yOz}$
Hoạt động 2 trang 70
Xác định các cạnh và đỉnh của các góc $\widehat{O_1}$ và $\widehat{O_3}$.
$\widehat{O_1}$ có cạnh $O x$ và Ot, đỉnh 0
$\widehat{O_3}$ có cạnh Oy và $\mathrm{Oz}$, đỉnh 0
Ta có: $\widehat{O_1}$ và $\widehat{O_3}$ có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
$\widehat{O_1}$ và $\widehat{O_3}$ có chung đỉnh
Thực hành 2 trang 70
b) Vẽ $\widehat{x O y}$ rồi vẽ $\widehat{t O z}$ đối đỉnh với $\widehat{x O y}$
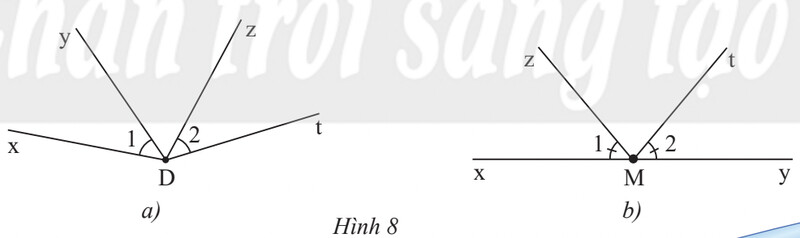
c) Cặp góc $\widehat{x D y}$ và $\widehat{z D t}$ trong Hình 8a và cặp góc $\widehat{x M z}$ và $\widehat{t M y}$ trong Hình 8b có phải là các cặp góc đối đỉnh hay không? Hãy giải thích tại sao.
Vẽ hình
Hai góc đối đỉnh là hai góc có chung gốc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
Chú ý: 2 đường thẳng cắt nhau tạo ra 2 cặp góc đối đỉnh
a)
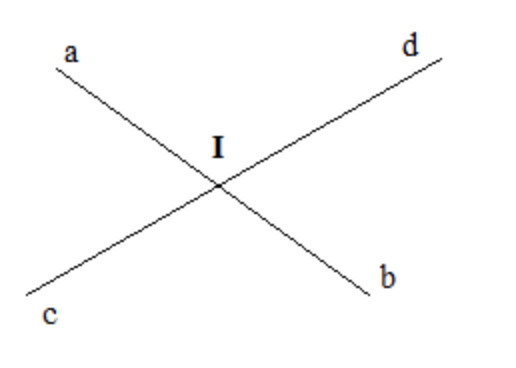
Các cặp góc đối đỉnh trên hình vẽ là: $\widehat{a I d}$ và $\widehat{b I c} ; \widehat{a I c}$ và $\widehat{b I d}$
b)
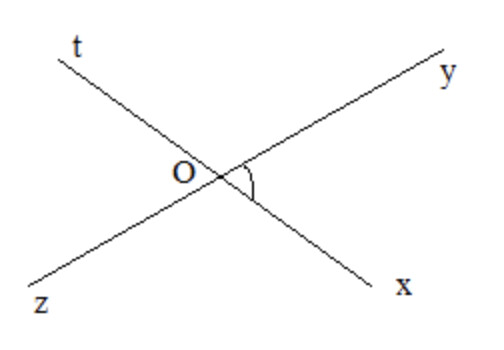
Bước 1: Vẽ góc $\widehat{x O y}$
Bước 2: Vẽ tia Ot là tia đối của tia $O x$
Bước 3: Vẽ tia Oz là tia đối của tia Oy
Ta được $\widehat{t O z}$ đối đỉnh với $\widehat{x O y}$
c) Cặp góc $\widehat{x D y}$ và $\widehat{z D t}$ trong Hình 8a và cặp góc $\widehat{x M z}$ và $\widehat{t M y}$ trong Hình 8b không phải là các cặp góc đối đỉnh vì mỗi cạnh của góc này không là cạnh đối của một cạnh của góc kia
ở Hình 8a, Dt không là tia đối của Dx hay Dy; Dz không là tia đối của Dx hay Dy ở Hình 8b, My là tia đối của $\mathrm{Mx}$ nhưng Mt không là tia đối của Mz
Vận dụng 2 trang 70
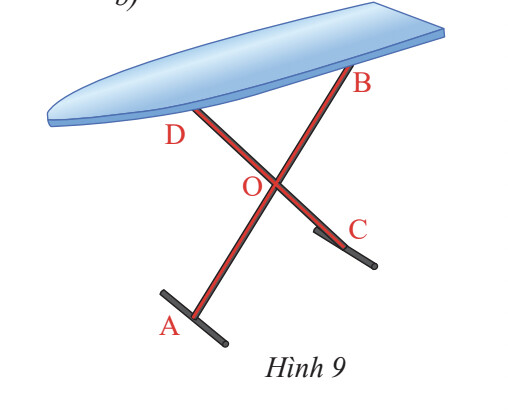
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia
Các góc đối đỉnh trong hình là: $ \widehat{D O B} \text { và } \widehat{C O A} ; \widehat{B O C} \text { và } \widehat{A O D}$
Hoạt động 3 trang 71
a) Hãy dùng thước đo góc đề đo $\widehat{\mathrm{O}}_{1}$ và $\widehat{\mathrm{O}}_{3}$.
So sánh số đo hai góc đó.
b) Hãy duing thước đo góc để đo $\widehat{\mathrm{O}}_{2}$ và $\widehat{\mathrm{O}}_{4}$.
So sánh số đo hai góc đó.
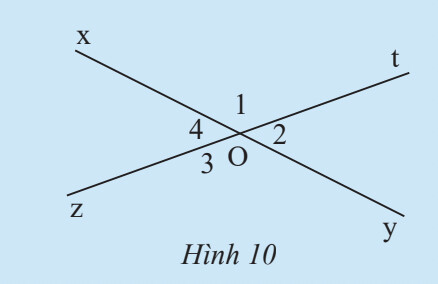
Đo góc bằng thước đo góc.
Ta có:
a) $\widehat{O_1}=135^{\circ} ; \widehat{O_3}=135^{\circ} \Rightarrow \widehat{O_1}=\widehat{O_3}$
b) $\widehat{O_2}=45^{\circ} ; \widehat{O_4}=45^{\circ} \Rightarrow \widehat{O_2}=\widehat{O_4}$
Thực hành 3 trang 71
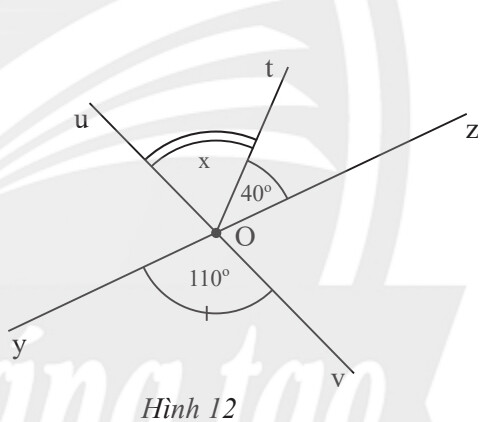
a) Tìm góc đối đỉnh của $\widehat{y O v}$
b) Tính số đo của $\widehat{u O z}$
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia
Hai góc đối đỉnh có số đo bằng nhau
a) Góc đối đỉnh của $\widehat{y O v}$ là $\widehat{z O u}$ vì tia Oz đối tia Oy, Ou đối tia Ov
b) Ta có: $\widehat{u O z}=\widehat{y O v}$ ( 2 góc đối đỉnh), mà $\widehat{y O v}=110^{\circ}$ nên $\widehat{u O z}=110^{\circ}$
Vận dụng 3 trang 71

Bước 1: Tìm số đo $\widehat{u O z}$
Bước 2: $\widehat{u O t}+\widehat{t O z}=\widehat{u O z}$ do $\widehat{u O t}, \widehat{t O z}$ là 2 góc kề nhau
Ta có: $\widehat{u O z}=\widehat{y O v}$ ( 2 góc đối đỉnh), mà $\widehat{y O v}=110^{\circ}$ nên $\widehat{u O z}=110^{\circ}$
Mà $\widehat{u O t}, \widehat{t O z}$ là 2 góc kề nhau nên $\widehat{u O t}+\widehat{t O z}=\widehat{u O z}$
$ \Rightarrow x+40^{\circ}=110^{\circ} $
$ \Rightarrow x=110^{\circ}-40^{\circ}=70^{\circ} $
Vậy $x=70^{\circ}$
Giải bài tập SGK bài Các góc ở vị trí đặc biệt
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Các góc ở vị trí đặc biệt trang 72 sách Toán 7 chân trời sáng tạo tập 1 dưới đây nhé!
Bài tập 1 trang 72
b) Tìm số đo cuia $\widehat{\mathrm{tOz}}$ nếu cho biêt
$\widehat{\mathrm{xOy}}=20^{\circ} ; \widehat{\mathrm{xOt}}=90^{\circ}$;
$ \widehat{\mathrm{yOz}}=\widehat{\mathrm{tOz}}$
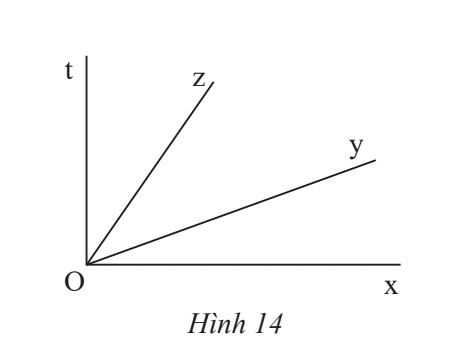
a) Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
b) Nếu $\widehat{u O t}, \widehat{t O z}$ là 2 góc kề nhau thì $\widehat{u O t}+\widehat{t O z}=\widehat{u O z}$
Lời giải chi tiết
a) Các góc kề với $\widehat{x O y}$ là: $\widehat{y O z} ; \widehat{y O t}$
b) Ta có:
$\widehat{x O y}+\widehat{y O z}+\widehat{z O t}=\widehat{x O t}$
$\Rightarrow 20^{\circ}+\widehat{z O t}+\widehat{z O t}=90^{\circ} $
$ \Rightarrow 2 . \widehat{z O t}=90^{\circ}-20^{\circ}=70^{\circ}$
$ \Rightarrow \widehat{z O t}=70^{\circ}: 2=35^{\circ}$
Bài tập 2 trang 72
2 góc bù nhau là 2 góc có tổng số đo bằng 180 độ
Vì hai góc $\widehat{x O y}, \widehat{y O z}$ kề bù với nhau nên
$ \widehat{x O y}+\widehat{y O z}=180^{\circ}$
$ \Rightarrow 25^{\circ}+\widehat{y O z}=180^{\circ}$
$\Rightarrow \widehat{y O z}=180^{\circ}-25^{\circ}=155^{\circ}$
Bài tập 3 trang 72
Nếu $\widehat{u O t}, \widehat{t O z}$ là 2 góc kề nhau thì $\widehat{u O t}+\widehat{t O z}=\widehat{u O z}$
Vì $\widehat{A O B}$ và $\widehat{B O C}$ là 2 góc kề nhau nên $\widehat{A O B}+\widehat{B O C}=\widehat{A O C}$, mà $\widehat{A O C}=80^{\circ}$ nên $\widehat{A O B}+\widehat{B O C}=80^{\circ}$
vì $\widehat{A O B}=\frac{1}{5} . \widehat{A O C}$ nên $\widehat{A O B}=\frac{1}{5} .80^{\circ}=16^{\circ}$
Như vậy,
$ 16^{\circ}+\widehat{B O C}=80^{\circ} $
$ \Rightarrow \widehat{B O C}=80^{\circ}-16^{\circ}=64^{\circ} $
Vậy $\widehat{A O B}=16^{\circ} ; \widehat{B O C}=64^{\circ}$
Bài tập 4 trang 72

Sử dụng tính chất:
+ Hai góc đối đỉnh thì bằng nhau
+ Hai góc kề bù có tổng số đo là 180 độ
a) Ta có: $b = 132^{\circ}$ ( 2 góc đối đỉnh)
$a+132^{\circ}=180^{\circ}$ (2 góc kề bù) nên $a=180^{\circ}-132^{\circ}=48^{\circ}$
$\mathrm{c}=\mathrm{a}=48^{\circ}(2$ góc đối đỉnh)
b) e = $21^{\circ}$ (2 góc đối đỉnh)
$\mathrm{d}+21^{\circ}=180^{\circ}$ (2 góc kề bù) nên $\mathrm{d}=180^{\circ}-21^{\circ}=159^{\circ}$
$\mathrm{f}=\mathrm{d}=159^{\circ}$ (2 góc đối đỉnh)
Bài tập 5 trang 72
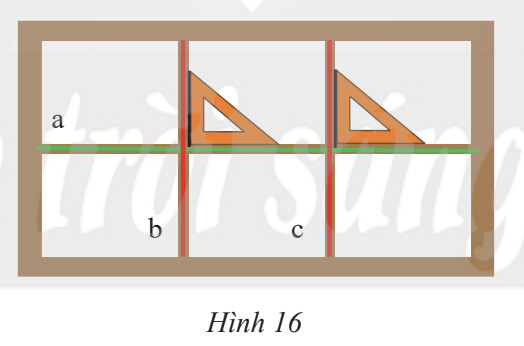
2 đường thẳng cắt nhau tạo thành 1 góc vuông thì 2 đường thẳng đó vuông góc.
Ta thấy: a ⊥b và a ⊥c
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 1 chương 4 – Góc và đường thẳng song song trang 69, 70, 71, 72 Toán 7 Chân trời sáng tạo tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




