Giải SGK bài 4 trang 59, 60, 61, 62, 63 chương 3 Toán 7 Chân trời sáng tạo tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác và lăng trụ đứng tứ giác. Các bài tập sau đây thuộc bài 4 chương 3 – Các hình khối trong thực tiễn trang 59, 60, 61, 62, 63 Toán 7 Chân trời sáng tạo tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài 4 chương 3
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 59, 60, 61 trong bài Diện tích xung quanh và thể tích hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 59
a) Tính tổng diện tích ba mặt bên của hình lăng trụ đứng.
b) Gọi Cđáy là chu vi đáy và h là chiều cao của hình lăng trụ, tính Cđáy . h.
c) So sánh kết quả của câu a và câu b.
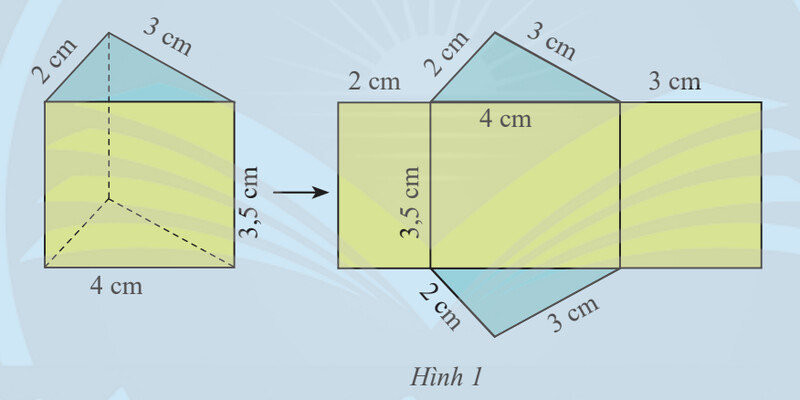
a) Hình lăng trụ đứng có ba mặt bên đều là hình chữ nhật:
– Mặt bên thứ nhất có dạng hình chữ nhật có chiều dài 3,5 cm và chiều rộng 2 cm nên có diện tích là:
$3,5 . 2 = 7 (cm^2)$.
– Mặt bên thứ hai có dạng hình chữ nhật có chiều dài 4 cm và chiều rộng 3,5 cm nên có diện tích là:
$4 . 3,5 = 14 (cm^2)$.
– Mặt bên thứ ba có dạng hình chữ nhật có chiều dài 3,5 cm và chiều rộng 3 cm nên có diện tích là:
$3,5 . 3 = 10,5 (cm^2)$.
Tổng diện tích ba mặt bên của hình lăng trụ đứng là:
$7 + 14 + 10,5 = 31,5 (cm^2)$.
Vậy tổng diện tích ba mặt bên của hình lăng trụ đứng là $31,5 cm^2$.
b) Chu vi đáy của hình lăng trụ đứng là:
$C_{\text {đáy }} = 2 + 3 + 4 = 9 (cm)$
Vậy $C_{\text {đáy }} . h = 9 . 3,5 = 31,5 (cm^2)$.
c) Kết quả thu được ở câu a và câu b đều bằng nhau.
Thực hành 1 trang 59
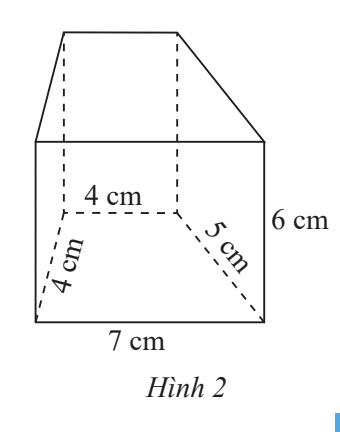
Hình lăng trụ đứng có đáy là hình thang được cho trong Hình 2 có chiều cao là $6 cm$.
Chu vi đáy của lăng trụ đứng là:
$4 + 4 + 5 + 7 = 20 (cm)$
Diện tích xung quanh của lăng trụ đứng là:
$20 . 6 = 120 (cm^2)$.
Vậy diện tích xung quanh của lăng trụ đứng trong Hình 2 là $120 cm^2$.
Hoạt động 2 trang 60
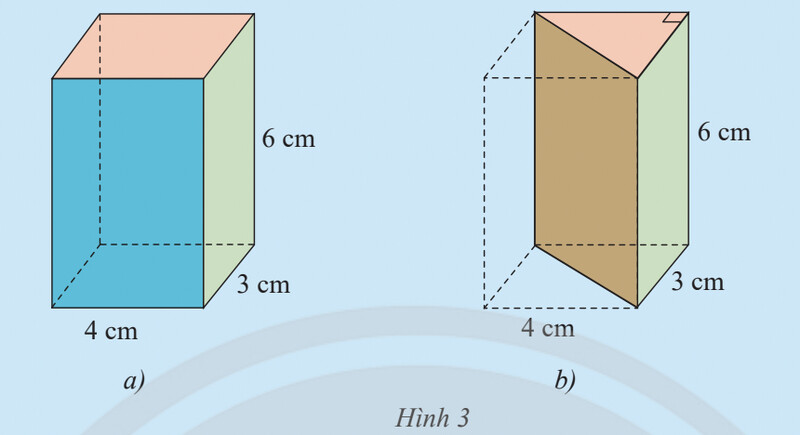 a) Tính thể tích của hình hộp chữ nhật.
a) Tính thể tích của hình hộp chữ nhật.b) Dự đoán thể tích của hình lăng trụ đứng tam giác dựa vào thể tích hình hộp chữ nhật ở câu a.
c) Gọi $S_{\text {đáy }}$ là diện tích mặt đáy và h là chiều cao của hình lăng trụ tam giác. Hãy tính $S_{\text {đáy }} . h$
d) So sánh $S_{\text {đáy }} . h$ và kết quả dự đoán ở câu b.
Thể tích của hình hộp chữ nhật có chiều dài đáy a, chiều rộng b, chiều cao c là: V = a.b.c
Diện tích hình chữ nhật có chiều dài a, chiều rộng b là: S = a.b
a) Thể tích của hình hộp chữ nhật là:
$4 . 3 . 6 = 72 (cm^3)$
b) Dự đoán: Thể tích của hình lăng trụ đứng tam giác bằng một nửa thể tích hình hộp chữ nhật.
c) Diện tích đáy của hình lăng trụ đứng tam giác là:
$12.3.4=6 (cm^2)$
Vậy $S_{\text {đáy }} . h = 6 . 6 = 36 (cm^3)$
d) Kết quả dự đoán ở câu b là đúng.
Thực hành 2 trang 60
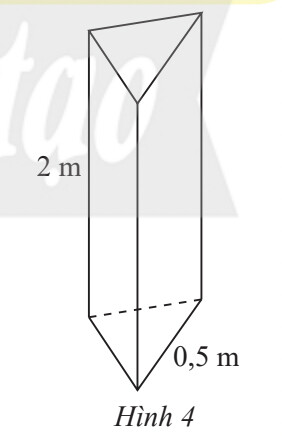
Diện tích xung quanh lăng trụ đứng = chu vi đáy. chiều cao
Diện tích xung quanh cột bê tông đó là:
$S_{x q}=C_{\text {đáy }} . h=(0,5+0,5+0,5). 2=3\left(m^2\right)$
Thực hành 3 trang 60
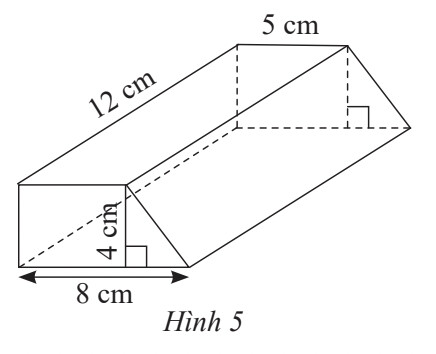
Thể tích hình lăng trụ là: V = Diện tích đáy . chiều cao
Diện tích hình thang có 2 đáy là a và b, chiều cao h là: S = (a+b).h : 2
Diện tích đáy của lăng trụ là:
$S_{\text {đáy }} = (5+8).4:2 = 26 (cm^2)$
Thể tích hình lăng trụ đứng trong Hình 5 là:
$V = S_{\text {đáy }}. h = 26 . 12 = 312 (cm^3)$
Thực hành 4 trang 61
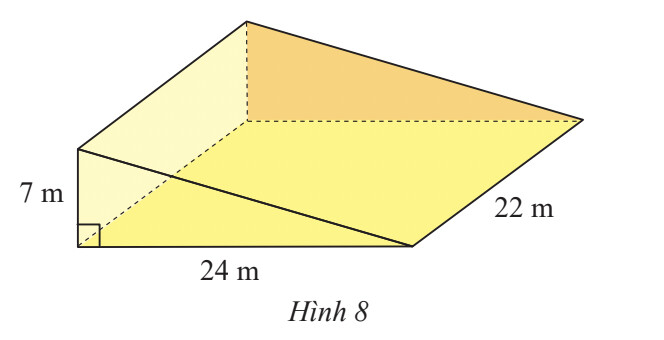
Thể tích lăng trụ đứng là: $V = S_{text{đáy}} . h$
Thể tích khối bê tông là: $ \mathrm{V}=\mathrm{S}_{\text {đáy }}. \mathrm{h}=\frac{1}{2} . 24. 7.22=1848\left(\mathrm{~m}^3\right)$
Vận dụng trang 62

Lăng trụ đứng có đáy là hình thang.
Bước 1: Tính $\mathrm{S}_{\mathrm{xq}}=\mathrm{C}_{\text {đáy }} \cdot \mathrm{h}$
Bước 2: Tính $S_{\text {đáy }}$
Bước 3: Diện tích phần cần sơn $=S_{x q}+S_{\text {đáy }}$
Diện tích xung quanh chiếc hộp là:
$\mathrm{S}_{\mathrm{xq}}=\mathrm{C}_{\text {đáy }} . \mathrm{h}=(6+4+8+4+10). 3=96\left(\mathrm{~cm}^2\right)$
Diện tích đáy là:
$S_{\text {đáy }}=(10+4) . 8: 2=56\left(\mathrm{~cm}^2\right)$
Diện tích phần cần sơn là:
$96+56=152\left(\mathrm{~cm}^2\right)$
Giải bài tập SGK bài 4 chương 3
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Diện tích xung quanh và thể tích hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác trang 62, 63 sách Toán 7 chân trời sáng tạo tập 1 dưới đây nhé!
Bài tập 1 trang 62
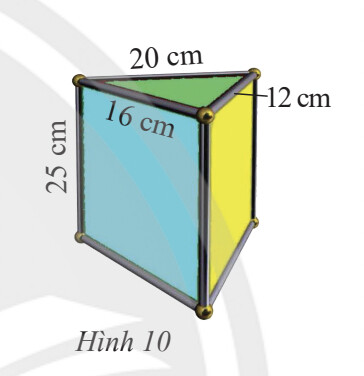
$S_{x q}=C_{\text {đáy }}. h$
Diện tích xung quanh của chiếc hộp là:
$S_{x q}=C_{\text {đáy }}. \mathrm{h}=(20+12+16) . 25=1200\left(\mathrm{~cm}^2\right)$
Bài tập 2 trang 62
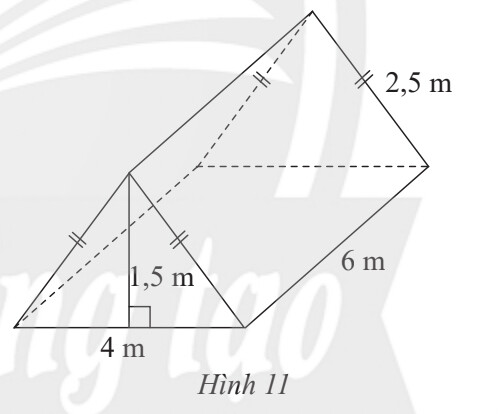
Diện tích tấm bạt $=\mathrm{S}_{\mathrm{xq}}+\mathrm{S}_{\text {đáy }}-S_{\text {đất }}$
(trong đó, $\mathrm{S}_{\mathrm{xq}}=\mathrm{C}_{\text {đáy }}. \mathrm{h}$ )
Thể tích lều là: $V=S_{\text {đáy }}. h$
Chú ý: Diện tích tam giác $=\frac{1}{2}$. Chiều cao. Đáy tương ứng
Diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) là:
$S=S_{x q}+2 . S_{\text {đáy }}-S_{\text {đất }}=(4+2,5+2,5). 6+2. \frac{1}{2} . 4 .1,5-6 . 4=36\left(\mathrm{~m}^2\right)$
Thể tích của chiếc lều là:
$V=S_{\text {đáy }} . h=\frac{1}{2} . 4 . 1,5 . 6=18\left(\mathrm{~m}^3\right)$
Bài tập 3 trang 62
a) Người ta muốn sơn tất cả các mặt của cái bục. Diện tích cần sơn là bao nhiêu?
b) Tính thể tích của cái bục.
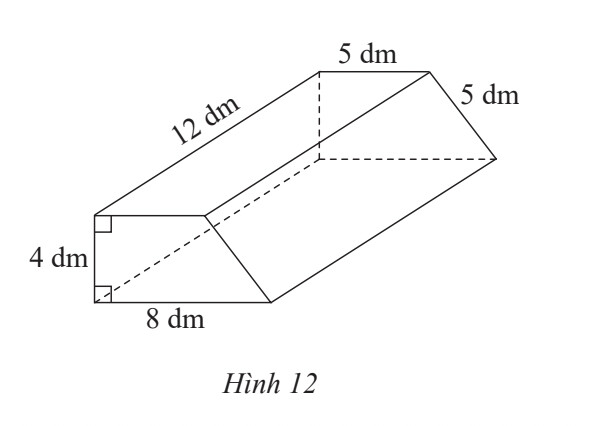
Bục là hình lăng trụ đứng có đáy là hình thang
Diện tích cần $s$ ơn $=S_{x q}+2 . S_{\text {đáy }}$
Thể tích bục là: $V=S_{\text {đáy }}. h$
a) Diện tích xung quanh của lăng trụ là: $(4+8+5+5) .12=264\left(\mathrm{dm}^2\right)$
Diện tích đáy của lăng trụ là: (5+8).4:2 = $26\left(\mathrm{dm}^2\right)$
Diện tích cần sơn là:
$\mathrm{S}_{\mathrm{xq}}+2 . \mathrm{S}_{\text {đáy }}=264+2.26=316\left(\mathrm{dm}^2\right)$
b) Thể tích bục là:
$\mathrm{V}=S_{\text {đáy }}. \mathrm{h}=26.12=312\left(\mathrm{dm}^3\right)$
Bài tập 4 trang 63
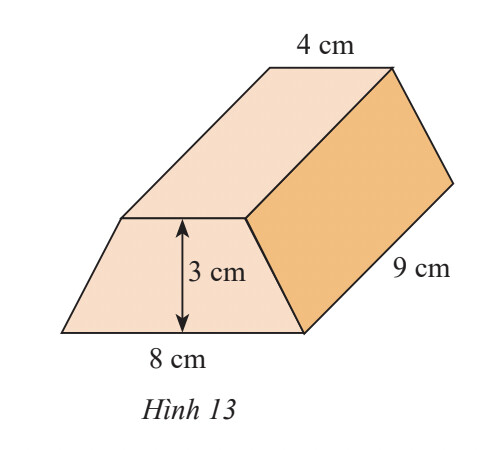
Thể tích lăng trụ đứng là: $V=S_{\text {đáy }}. \mathrm{h}$
S hình thang = (đáy lớn + đáy nhỏ). Chiều cao : 2
Diện tích đáy là:
$(8+4) . 3: 2=18\left(\mathrm{~cm}^2\right)$
Thể tích lăng trụ đứng là:
$V=S_{\text {đáy }} .h=18.9=162\left(\mathrm{~cm}^3\right)$
Bài tập 5 trang 63
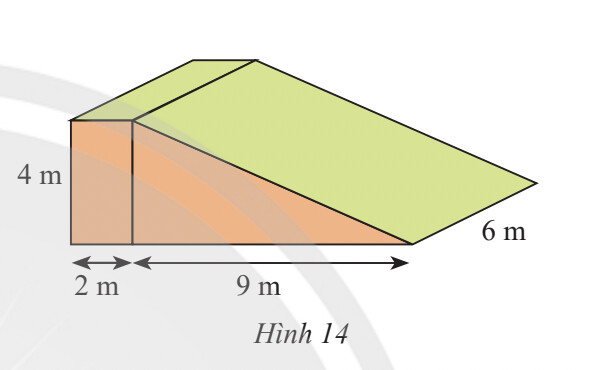
Khối bê tông là hình lăng trụ có đáy là hình thang, chiều cao 6 m Tính thể tích lăng trụ đứng là: $V=S_{\text {đáy }} \cdot h$
Chi phí = thể tích . giá đúc $1 \mathrm{~m}^3$
Diện tích đáy hình thang là: (2+2+9).4:2 = $26\left(\mathrm{~m}^2\right)$
Thể tích khối bê tông đó là:
$V=S_{\text {đáy }}. h=26.6=156\left(\mathrm{~m}^3\right)$
Chi phí để đúc khối bê tông đó là:
$156 . 1,2 = 187,2$ (triệu đồng)
Bài tập 6 trang 63
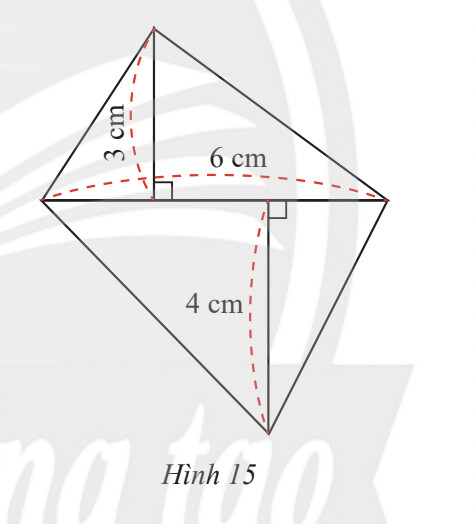
Tính diện tích đáy của lăng trụ = Tổng diện tích 2 tam giác (Trong đó, diện tích tam giác $=\frac{1}{2}$. Chiều cao. Đáy tương ứng)
Tính thể tích lăng trụ đứng là: $V=S_{\text {đáy }}. h$
Diện tích đáy của lăng trụ là:
$\frac{1}{2} .3 .6+\frac{1}{2} .4 .6=21\left(\mathrm{~cm}^2\right)$
Tính thể tích lăng trụ đứng là:
$\mathrm{V}=\mathrm{S}_{\text {đáy }} . \mathrm{h}=21.7=147\left(\mathrm{~cm}^3\right)$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 4 chương 3 – Các hình khối trong thực tiễn trang 59, 60, 61, 62, 63 Toán 7 Chân trời sáng tạo tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




