SGK Toán 7 – Chân Trời Sáng Tạo
Giải SGK bài tập cuối chương 3 Toán 7 Chân trời sáng tạo Tập 1
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những bài tập tự luận trong bài tập ôn tập cuối chương 3. Đây là Bài tập cuối chương 3 trang 66, 67 sách Toán 7 Chân trời sáng tạo tập 1. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Bài 1 trang 66
Một hình khối gồm $14$ hình lập phương gắn kết với nhau như Hình 1. Mỗi hình lập phương cạnh $1 cm$. Hãy tính thể tích của hình khối này.
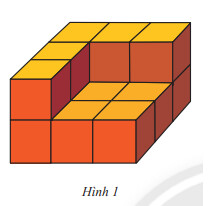

Phương pháp giải:
Thể tích khối hình = tổng thể tích của các hình lập phương nhỏ
Thể tích hình lập phương cạnh $a$ là: $a^3$
Thể tích khối hình = tổng thể tích của các hình lập phương nhỏ
Thể tích hình lập phương cạnh $a$ là: $a^3$
Lời giải chi tiết:
Thể tích mỗi hình lập phương là: $V=1^3=1\left(\mathrm{~cm}^3\right)$
Thể tích của hình khối này là:
$$V=14.1=14\left(\mathrm{~cm}^3\right)$$
Thể tích mỗi hình lập phương là: $V=1^3=1\left(\mathrm{~cm}^3\right)$
Thể tích của hình khối này là:
$$V=14.1=14\left(\mathrm{~cm}^3\right)$$
Bài 2 trang 66
Một bể cá hình hộp chữ nhật với kích thước mặt đáy là $5 dm$ và $12 dm$, có mực nước là $7 dm$. Người ta đổ vào đó một lượng cát (có độ thấm nước không đáng kể) thì thấy mực nước dâng thêm $1,5 dm$ và ngập cát đổ vào. Tính thể tích của lượng cát.
Phương pháp giải:
Cách 1:
Bước 1: Tính thể tích mực nước ban đầu
Bước 2: Tính thể tích nước và cát sau khi đổ cát
Bước 3: Tính thể tích cát đổ vào = thể tích sau khi đổ cát – thể tích mực nước ban đầu
Cách 2:
Thể tích lượng cát = thể tích hình hộp có kích thước mặt đáy là $5 dm$ và $12 dm$, chiều cao $1,5 dm$
Chú ý: Thể tích hình hộp chữ nhật có kích thước $a,b,c$ là: $V= a.b.c$
Cách 1:
Bước 1: Tính thể tích mực nước ban đầu
Bước 2: Tính thể tích nước và cát sau khi đổ cát
Bước 3: Tính thể tích cát đổ vào = thể tích sau khi đổ cát – thể tích mực nước ban đầu
Cách 2:
Thể tích lượng cát = thể tích hình hộp có kích thước mặt đáy là $5 dm$ và $12 dm$, chiều cao $1,5 dm$
Chú ý: Thể tích hình hộp chữ nhật có kích thước $a,b,c$ là: $V= a.b.c$
Lời giải chi tiết:
Cách 1:
Thể tích mực nước ban đầu là:
$$v_1=5.12 .7=420\left(\mathrm{dm}^3\right)$$
Thể tích nước và cát sau khi đổ cát là:
$$V_2=5.12.(7+1,5)=510\left(\mathrm{dm}^3\right)$$
Thể tích cát đổ vào là:
$$V=V_2-V_1=510-420=90\left(\mathrm{dm}^3\right)$$
Cách 2:
Thể tích cát đổ vào là: $5.12.1,5 = 90\left(\mathrm{dm}^3\right)$
Cách 1:
Thể tích mực nước ban đầu là:
$$v_1=5.12 .7=420\left(\mathrm{dm}^3\right)$$
Thể tích nước và cát sau khi đổ cát là:
$$V_2=5.12.(7+1,5)=510\left(\mathrm{dm}^3\right)$$
Thể tích cát đổ vào là:
$$V=V_2-V_1=510-420=90\left(\mathrm{dm}^3\right)$$
Cách 2:
Thể tích cát đổ vào là: $5.12.1,5 = 90\left(\mathrm{dm}^3\right)$
Bài 3 trang 66
Một khuôn đúc bê tông có kích thước như Hình 2. Bề dày các mặt bên của khuôn là $1,2 cm$. Bề dày mặt đáy của khuôn là $1,9 cm$. Thể tích của khối bê tông được khuôn này đúc ra là bao nhiêu xăng ti mét khối?
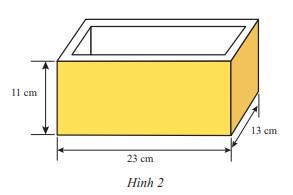

Phương pháp giải:
Tính chiều dài, chiều rộng, chiều cao của lõi khuôn
Thể tích khối bê tông được khuôn này đúc ra = thể tích lõi khuôn
Chú ý: Lõi khuôn là hình hộp chữ nhật
Tính chiều dài, chiều rộng, chiều cao của lõi khuôn
Thể tích khối bê tông được khuôn này đúc ra = thể tích lõi khuôn
Chú ý: Lõi khuôn là hình hộp chữ nhật
Lời giải chi tiết:
Chiều dài của lỗi khuôn là: $23 – 1,2 – 1,2 = 20,6 (cm)$
Chiều rộng của lõi khuôn là: $13 – 1,2 – 1,2 = 10,6 (cm)$
Chiều cao của lõi khuôn là: $11 – 1,9 = 9,1 (cm)$
Thể tích khối bê tông được khuôn này đúc ra là:
$$V=20,6.10,6.9,1=1987,076\left(\mathrm{~cm}^3\right)$$
Chiều dài của lỗi khuôn là: $23 – 1,2 – 1,2 = 20,6 (cm)$
Chiều rộng của lõi khuôn là: $13 – 1,2 – 1,2 = 10,6 (cm)$
Chiều cao của lõi khuôn là: $11 – 1,9 = 9,1 (cm)$
Thể tích khối bê tông được khuôn này đúc ra là:
$$V=20,6.10,6.9,1=1987,076\left(\mathrm{~cm}^3\right)$$
Bài 4 trang 66
Phần bên trong của một cái khuôn làm bánh có dạng hình hộp chữ nhật với đáy là hình vuông cạnh $20 cm$, chiều cao $5 cm$ ( Hình 3). Người ta dự định sơn phần bên trong bằng loại sơn không dính. Hỏi với một lượng sơn đủ bao phủ được $100 m2$ thì sơn được bao nhiêu cái khuôn làm bánh?
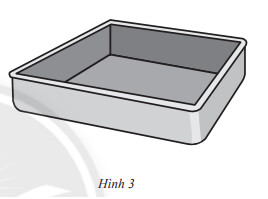

Phương pháp giải:
Tính diện tích xung quanh của phần bên trong khuôn: $S_{x q}=C_{\text {đáy }} \cdot h$
Diện tích phần cần sơn = diện tích xung quanh + diện tích đáy
Số khuôn bánh = diện tích bao phủ được : diện tích 1 khuôn
Tính diện tích xung quanh của phần bên trong khuôn: $S_{x q}=C_{\text {đáy }} \cdot h$
Diện tích phần cần sơn = diện tích xung quanh + diện tích đáy
Số khuôn bánh = diện tích bao phủ được : diện tích 1 khuôn
Lời giải chi tiết:
Diện tích cần sơn của mỗi khuôn là:
$$\mathrm{S}=\mathrm{S}_{\mathrm{xq}}+\mathrm{S}_{\text {đáy }}=\mathrm{C}_{\text {đáy }} \cdot \mathrm{h}+\mathrm{S}_{\text {đáy }}=(4.20).5+20.20=800\left(\mathrm{~cm}^2\right)=0,08 \mathrm{~m}^2$$
Số khuôn bánh sơn được là:
$$100: 0,08=1250(\text { cái })$$
Chú ý: Đổi về cùng đơn vị
Diện tích cần sơn của mỗi khuôn là:
$$\mathrm{S}=\mathrm{S}_{\mathrm{xq}}+\mathrm{S}_{\text {đáy }}=\mathrm{C}_{\text {đáy }} \cdot \mathrm{h}+\mathrm{S}_{\text {đáy }}=(4.20).5+20.20=800\left(\mathrm{~cm}^2\right)=0,08 \mathrm{~m}^2$$
Số khuôn bánh sơn được là:
$$100: 0,08=1250(\text { cái })$$
Chú ý: Đổi về cùng đơn vị
Bài 5 trang 66
Một ngôi nhà có kích thước như Hình 4.
a) Tính thể tích của ngôi nhà.
b) Biết rằng $1l$ sơn bao phủ được $4 \mathrm{~m}^2$ tường. Hỏi phải cần ít nhất bao nhiêu lít sơn để sơn phủ được tường mặt ngoài ngôi nhà? (không sơn cửa)? Biết tổng diện tích các cửa là $9 \mathrm{~m}^2$.
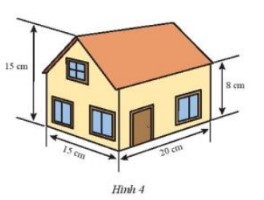
a) Tính thể tích của ngôi nhà.
b) Biết rằng $1l$ sơn bao phủ được $4 \mathrm{~m}^2$ tường. Hỏi phải cần ít nhất bao nhiêu lít sơn để sơn phủ được tường mặt ngoài ngôi nhà? (không sơn cửa)? Biết tổng diện tích các cửa là $9 \mathrm{~m}^2$.

Phương pháp giải:
Chia ngôi nhà thành 1 hình hộp chữ nhật và 1 hình lăng trụ tam giác
a) Thể tích ngôi nhà = thể tích hình hộp + thể tích lăng trụ tam giác
b) Diện tích cần sơn = diện tích xung quanh hình hộp + diện tích 2 đáy lăng trụ – diện tích các cửa
Chia ngôi nhà thành 1 hình hộp chữ nhật và 1 hình lăng trụ tam giác
a) Thể tích ngôi nhà = thể tích hình hộp + thể tích lăng trụ tam giác
b) Diện tích cần sơn = diện tích xung quanh hình hộp + diện tích 2 đáy lăng trụ – diện tích các cửa
Lời giải chi tiết:
Chia ngôi nhà thành 1 hình hộp chữ nhật với đáy có chiều dài $20 \mathrm{~m}$, chiều rộng $15 \mathrm{~m}$; chiều cao $8 m$ và 1 hình lăng trụ tam giác có đáy là tam giác có đáy là $15 m$, chiều cao tương ứng là $15-8=7 \mathrm{~m}$; chiều cao lăng trụ là $20 \mathrm{~m}$.
a) Thể tích ngôi nhà là:
V= V_{hh}+V_{lt} = 20.15.8+ \frac{\mathrm{1} }{\mathrm{2}}.15.20.7=3450( m^3 )
b) Diện tích xung quanh hình hộp là:
$$S_{x q}=2 \cdot(15+20) \cdot 8=560\left(m^2\right)$$
Diện tích 2 đáy của lăng trụ tam giác là:
$2 . \frac{1}{2} \cdot 15.7=105\left(m^2\right)$
Diện tích cần sơn là:
$$560+105-9=656\left(m^2\right)$$
Số lít sơn cần dùng là:
$656: 4=164(l)$
Đáp số:
a) $3450 \mathrm{~m}^3$
b) $164 lít$
Chia ngôi nhà thành 1 hình hộp chữ nhật với đáy có chiều dài $20 \mathrm{~m}$, chiều rộng $15 \mathrm{~m}$; chiều cao $8 m$ và 1 hình lăng trụ tam giác có đáy là tam giác có đáy là $15 m$, chiều cao tương ứng là $15-8=7 \mathrm{~m}$; chiều cao lăng trụ là $20 \mathrm{~m}$.
a) Thể tích ngôi nhà là:
V= V_{hh}+V_{lt} = 20.15.8+ \frac{\mathrm{1} }{\mathrm{2}}.15.20.7=3450( m^3 )
b) Diện tích xung quanh hình hộp là:
$$S_{x q}=2 \cdot(15+20) \cdot 8=560\left(m^2\right)$$
Diện tích 2 đáy của lăng trụ tam giác là:
$2 . \frac{1}{2} \cdot 15.7=105\left(m^2\right)$
Diện tích cần sơn là:
$$560+105-9=656\left(m^2\right)$$
Số lít sơn cần dùng là:
$656: 4=164(l)$
Đáp số:
a) $3450 \mathrm{~m}^3$
b) $164 lít$
Bài 6 trang 67
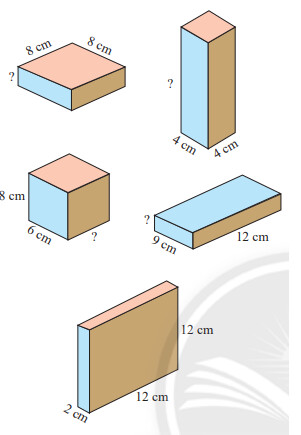
Các hình hộp chữ nhật trong Hình 5 có cùng số đo thể tích. Em hãy tìm các kích thước còn thiếu.

Phương pháp giải:
Bước 1: Tính thể tích hình hộp = chiều dài. Chiều rộng . chiều cao
Bước 2: Tìm kích thước còn thiếu trong các hình
Bước 1: Tính thể tích hình hộp = chiều dài. Chiều rộng . chiều cao
Bước 2: Tìm kích thước còn thiếu trong các hình
Lời giải chi tiết:
Thể tích mỗi hình hộp chữ nhật là: $V=2.12 .12=288\left(\mathrm{~cm}^3\right)$
Xét hình $5 a: ?=288: 8: 8=4,5 \mathrm{~cm}$
Xét hình $5b: ?=288: 4: 4=18 \mathrm{~cm}$
Xét hình $5 c: ?=288: 8: 6=6 \mathrm{~cm}$
Xét hình $5d: ? =288: 12: 9=\frac{8}{3} \mathrm{~cm}$
Thể tích mỗi hình hộp chữ nhật là: $V=2.12 .12=288\left(\mathrm{~cm}^3\right)$
Xét hình $5 a: ?=288: 8: 8=4,5 \mathrm{~cm}$
Xét hình $5b: ?=288: 4: 4=18 \mathrm{~cm}$
Xét hình $5 c: ?=288: 8: 6=6 \mathrm{~cm}$
Xét hình $5d: ? =288: 12: 9=\frac{8}{3} \mathrm{~cm}$
Bài 7 trang 67
Tạo lập hình lăng trụ đứng có chiều cao $2,5 \mathrm{~cm}$, đáy là hình thoi có cạnh $3 \mathrm{~cm}$ và một góc $60^0$
Phương pháp giải:
– Vẽ 4 hình chữ nhật với kích thước $3 \mathrm{~cm} \times 2,5 \mathrm{~cm}$
– Gấp các cạnh $\mathrm{BN}, \mathrm{CP}$ và $\mathrm{DQ}$ sao cho cạnh $AM$ trùng với $A’M’$, một góc bằng $60$, ta được hình lăng trụ đứng $ABCD.MNPQ$ cần tạo lập
– Vẽ 4 hình chữ nhật với kích thước $3 \mathrm{~cm} \times 2,5 \mathrm{~cm}$
– Gấp các cạnh $\mathrm{BN}, \mathrm{CP}$ và $\mathrm{DQ}$ sao cho cạnh $AM$ trùng với $A’M’$, một góc bằng $60$, ta được hình lăng trụ đứng $ABCD.MNPQ$ cần tạo lập
Lời giải chi tiết:
Bước 1: Vẽ 4 hình chữ nhật với kích thước $3 \mathrm{~cm} \times 2,5 \mathrm{~cm}$
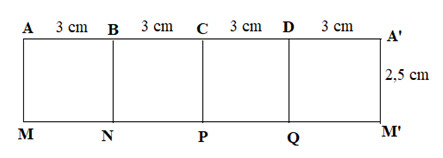
Bước 2: Gấp các cạnh $\mathrm{BN}, \mathrm{CP}$ và $\mathrm{DQ}$ sao cho cạnh $AM$ trùng với $A’M’$, một góc bằng $60$, ta được hình lăng trụ đứng $ABCD.MNPQ$ cần tạo lập.
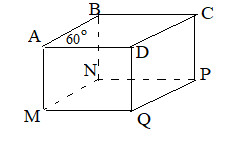
Bước 1: Vẽ 4 hình chữ nhật với kích thước $3 \mathrm{~cm} \times 2,5 \mathrm{~cm}$

Bước 2: Gấp các cạnh $\mathrm{BN}, \mathrm{CP}$ và $\mathrm{DQ}$ sao cho cạnh $AM$ trùng với $A’M’$, một góc bằng $60$, ta được hình lăng trụ đứng $ABCD.MNPQ$ cần tạo lập.

Bài 8 trang 67
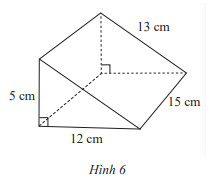
Hãy nêu các bước tạo lập hình lăng trụ đứng tam giác trong Hình 6.

Phương pháp giải:
Tạo lập hình lăng trụ đứng có chiều cao $15 cm$, đáy là tam giác vuông có 3 cạnh là $5 cm, 12 cm, 13 cm$:
– Vẽ 3 hình chữ nhật với kích thước $15 cm$ x $5 cm$; $15 cm$ x $12 cm$ và $15 cm$ x $13 cm$
– Gấp các cạnh $BN$ và $CP$ sao cho cạnh $AM$ trùng với $A’M’$, đáy có một góc vuông, ta được hình lăng trụ đứng tam giác $ABC.MNP$
Tạo lập hình lăng trụ đứng có chiều cao $15 cm$, đáy là tam giác vuông có 3 cạnh là $5 cm, 12 cm, 13 cm$:
– Vẽ 3 hình chữ nhật với kích thước $15 cm$ x $5 cm$; $15 cm$ x $12 cm$ và $15 cm$ x $13 cm$
– Gấp các cạnh $BN$ và $CP$ sao cho cạnh $AM$ trùng với $A’M’$, đáy có một góc vuông, ta được hình lăng trụ đứng tam giác $ABC.MNP$
Lời giải chi tiết:
Bước 1: Vẽ 3 hình chữ nhật với kích thước $15 cm$ x $5 cm$; $15 cm$ x $12 cm$ và $15 cm$ x $13 cm$
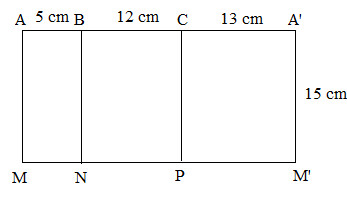
Bước 2: Gấp các cạnh $BN$ và $CP$ sao cho cạnh $AM$ trùng với $A’M’$, đáy có một góc vuông, ta được hình lăng trụ đứng tam giác $ABC.MNP$
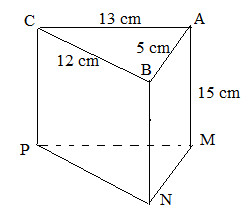
Bước 1: Vẽ 3 hình chữ nhật với kích thước $15 cm$ x $5 cm$; $15 cm$ x $12 cm$ và $15 cm$ x $13 cm$

Bước 2: Gấp các cạnh $BN$ và $CP$ sao cho cạnh $AM$ trùng với $A’M’$, đáy có một góc vuông, ta được hình lăng trụ đứng tam giác $ABC.MNP$

Bài 9 trang 67
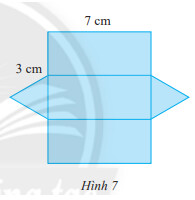
Người ta cắt một tấm bìa để tạo lập một lăng trụ đứng có đáy là tam giác đều với kích thước như Hình 7. Hãy cho biết độ dài các cạnh đáy và chiều cao của hình lăng trụ đứng.

Phương pháp giải:
Các cạnh không phải cạnh đáy thì là cạnh bên của lăng trụ đứng.
Độ dài cạnh bên của lăng trụ đứng là chiều cao.
Các cạnh không phải cạnh đáy thì là cạnh bên của lăng trụ đứng.
Độ dài cạnh bên của lăng trụ đứng là chiều cao.
Lời giải chi tiết:
Ta thấy đáy của hình lăng trụ là tam giác đều cạnh $3 cm$
Độ dài các cạnh đáy là $3 cm$
Chiều cao của hình lăng trụ là $7 cm$.
Ta thấy đáy của hình lăng trụ là tam giác đều cạnh $3 cm$
Độ dài các cạnh đáy là $3 cm$
Chiều cao của hình lăng trụ là $7 cm$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài tập cuối chương 3 Toán 7 Chân trời sáng tạo tập 1 ở các trang 66, 67. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!





