Giải SGK bài Số vô tỉ và căn bậc hai số học chương 2 Toán 7 Chân trời sáng tạo tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Số vô tỉ, căn bậc hai số học. Các bài tập sau đây thuộc bài 1 chương 2 – Số thực trang 30, 31, 32, 33, 34 Toán 7 Chân trời sáng tạo tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Số vô tỉ, căn bậc hai số học
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 30, 31, 32, 33 trong bài Số vô tỉ, căn bậc hai số học. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 30
$3: 2=? ; \quad 37: 25=? ; \quad 5: 3=? ; \quad 1: 9=?$.
b) Dùng kết quả trên để viết các số $\frac{3}{2} ; \frac{37}{25} ; \frac{5}{3} ; \frac{1}{9}$ dưới dạng số thập phân.
a)Thực hiện phép chia và viết kết quả các phép tính
b) Lấy kết quả của câu a để viết các phân số đã cho dưới dạng số thập phân
a) $3: 2=1,5 \quad 37: 25=1,48 \quad 5: 3=1,666 \ldots \quad 1: 9=0,111 \ldots$
b) $\frac{3}{2}=1,5 ; \quad \frac{37}{25}=1,48$ ;
$ \frac{5}{3}=1,666 \ldots ; \quad \frac{1}{9}=0,111 \ldots$
Thực hành 1 trang 31
Thực hiện phép chia, thu được kết quả là số thập phân
$\frac{12}{25}=0,48 ; \quad \frac{27}{2}=13,5 ; \quad \frac{10}{9}=1,(1)$
Vận dụng 1 trang 31
-Viết phân số $\frac{5}{6}$ dưới dạng số thập phân
-So sánh hai số thập phân
-Kết luận
Ta có $\frac{5}{6}=0,8(3)=0,8333 \ldots$
Vì: $0,834>0,8333 \ldots \Rightarrow 0,834>\frac{5}{6}$
Hoạt động 2 trang 31
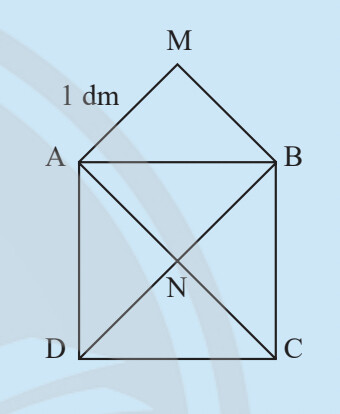
Cho biết cạnh $\mathrm{AM}=1 \mathrm{dm}$.
– Em hãy cho biết diện tích hinh vuông $\mathrm{ABCD}$ gấp mấy lần diện tích hình vuông AMBN.
– Tính diện tich hinh vuông $\mathrm{ABCD}$.
– Hãy biểu diễn diện tích hinh vuông $\mathrm{ABCD}$ theo độ dài đoạn $\mathrm{AB}$.
Diện tích hình vuông cạnh a là: $a^2$
– Các tam giác AMB, ABN, AND, DNC, CNB có diện tích bằng nhau.
Diện tích hình vuông AMCD bằng 2 lần diện tích tam giác ANB, diện tích hình vuông ABCD bằng 4 lần diện tích tam giác ANB nên
Diện tích hình vuông ABCD gấp 2 lần diện tích hình vuông AMCD.
– Diện tích hình vuông ABCD là: $2.12=2 (dm^2)$
– Diện tích hình vuông ABCD bằng $AB^2$
Thực hành 2 trang 32
a) Số $a=5,123$ là một số thập phân hữu hạn nên a là số .?.
b) Số $b = 6,15555… = 6,1(5)$ là một số thập phân vô hạn tuần hoàn nên b là số .?.
c) Người ta chứng minh được $\pi=3,14159265…$
là một số thập phân vô hạn không tuần hoàn. Vậy $\pi$ là số ?.
d) Cho biết số $c=2,23606… $ là một số thập phân vô hạn không tuần hoàn. Vậy c là số .?.
Sử dụng khái niệm số vô tỉ: Mỗi số thập phân vô hạn không tuần hoàn là biểu diễn thập phân của một số, số đó gọi là số vô tỉ.
a) Số $a=5,123$ là một số thập phân hữu hạn nên a là số hữu tỉ
b) Số $b = 6,15555… = 6,1(5)$ là một số thập phân vô hạn tuần hoàn nên b là số hữu tỉ
c) Người ta chứng minh được $\pi=3,14159265…$ là một số thập phân vô hạn không tuần hoàn. Vậy $\pi$ là số vô tỉ
d) Cho biết số $c=2,23606… $là một số thập phân vô hạn không tuần hoàn. Vậy c là số vô tỉ
Hoạt động 3 trang 32
b) Tìm số thực không âm $x$ với $x^2$ lần lượt bằng $4; 9; 16; 25; 100$.
a) Bình phương các số đã cho
b) Tìm các số thực không âm thỏa mãn đề bài
a) $x=2$ ta được $x^2=4 $
$ x=3$ ta được x^2=9$
$ x=4$ ta được $ x^2=16$
$ x=5$ ta được $ x^2=25 $
$ x=10$ ta được $ x^2=100$
b) $x^2=4$, ta được $x=2$;
$x^2=9$, ta được $x=3$;
$x^2=16$, ta được $x=4$;
$x^2=25$, ta được $x=5$;
$x^2=100$, ta được $x=10$
Thực hành 3 trang 32
Căn bậc hai số học của số a không âm là số x không âm sao cho $x^2 = a$.
Ta dùng kí hiệu $\sqrt{a}$ và để chỉ căn bậc hai số học của $a$.
Căn bậc hai số học của: $16; 7; 10; 36 $ lần lượt là $ 4 ; \sqrt{7} ; \sqrt{10} ; 6$
Vận dụng 2 trang 32
Độ dài cạnh bằng căn bậc hai số học của diện tích.
Độ dài cạnh là: $\sqrt{169}=13(m)$
Hoạt động 4 trang 33

Em hãy đọc kết quả trên màn hình rồi tính $x^2$
b) Sử dụng máy tính cầm tay bấm liên tiếp các nút

Em hãy đọc kết quả trên màn hình rồi tính $x^2$.
a) Kết quả trên màn hình là: 5
Suy ra: $x^2=5^2=25$
b) Kết quả trên màn hình là: $1,41421 \ldots$
Suy ra: $x^2=2$
Thực hành 4 trang 33
$\sqrt{3} ; \sqrt{15129} ; \sqrt{10000} ; \sqrt{10}$.
Dùng máy tính cầm tay để tính các căn bậc hai số học đã cho
$\sqrt{3} \approx 1,732 \ldots ; \sqrt{15129}=123 ; \quad \sqrt{10000}=100 ; \quad \sqrt{10} \approx 3,162 \ldots$
Vận dụng 3 trang 33
a) Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 12996 m²
b) Công thức tính diện tích $\mathrm{S}$ của hình tròn bán kính $\mathrm{R}$ là $S=\pi R^2$. Tính bán kính của một hình tròn có diện tích là $100 \mathrm{~cm}^2$.
a) Độ dài cạnh bằng căn bậc hai số học của diện tích.
b) Áp dụng công thức: $R=\sqrt{\frac{S}{\pi}}$
a) Độ dài cạnh của một mảnh đất hình vuông là:
$\sqrt{12996}=114(\mathrm{~m})$
b) Bán kính của hình tròn là:
$S=\pi R^2 \Rightarrow R^2=\frac{S}{\pi} \Rightarrow R=\sqrt{\frac{S}{\pi}}=\sqrt{\frac{100}{\pi}} \approx 5,64(\mathrm{~cm})$
Giải bài tập SGK bài Số vô tỉ, căn bậc hai số học
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Số vô tỉ, căn bậc hai số học trang 32, 33 sách Toán 7 chân trời sáng tạo tập 1 dưới đây nhé!
Bài tập 1 trang 33
$\frac{15}{8} ; \quad-\frac{99}{20} ; \quad \frac{40}{9} ; \quad-\frac{44}{7}$
b) Trong các số thập phân vừa tính được, hãy chi ra các số thập phân vô hạn tuần hoàn.
a) Thực hiện phép chia tử cho mẫu số để viết các số đã cho dưới dạng số thập phân.
b) Các số thập phân vô hạn không tuần hoàn là các số thập phân vô hạn mà ở phần thập phân không có một chu kì nào cả.
a)$ \frac{15}{8}=1,875 ; \quad \frac{-99}{20}=-4,95$
$ \frac{40}{9}=4,(4) ; \quad-\frac{44}{7}=-6,(285714)$
b) Trong các số thập phân trên, số thập phân 4,(4) và -6,(285714) là các số thập phân vô hạn tuần hoàn với chu kì lần lượt là 4 và $285714$
Bài tập 2 trang 33
a) $\sqrt{2} \in I$
b) $\sqrt{9} \in I$
c) $\pi \in I$
d) $\sqrt{4} \in \mathbb{Q}$
I là kí hiệu tập hợp các số vô tỉ
Q là kí hiệu tập hợp các số hữu tỉ
a) $\sqrt{2} \approx 1,1412 \ldots \in I$
b) $\sqrt{9}=3 \notin I$
c) $\pi \approx 3,141 \ldots \in I$
d) $\sqrt{4}=2 \in \mathbb{Q}$
Vậy các phát biểu a,c,d đúng.
Bài tập 3 trang 33
a) $\sqrt{64}$
b) $\sqrt{25^2}$
c) $\sqrt{(-5)^2}$
$\sqrt{a^2}=\sqrt{(-a)^2}=a \text { với } a \geq 0$
a) $\sqrt{64}=\sqrt{8^2}=8$
b) $\sqrt{25^2}=25$
c) $\sqrt{(-5)^2}=5$.
Bài tập 4 trang 33

$\sqrt{a^2}=a \text { với } a \geq 0$

Bài tập 5 trang 34
a) $\sqrt{2250}$;
b) $\sqrt{12}$
c) $\sqrt{5}$
d) $\sqrt{624}$
a) $\sqrt{2250} \approx 47,434$
b) $\sqrt{12} \approx 3,461$
c) $\sqrt{5} \approx 2,236$
d) $\sqrt{624} \approx 24,980$
Bài tập 6 trang 34
-Diện tích của sân = gia tiền thuê lát sân : chi phí lát $1 m^2$
-Chiều dài của sân bằng căn bậc hai số học của diện tích sân.
Diện tích của sân là: $10 125 000 : 125 000 = 81(m^2)$
Chiều dài cạnh của sân là: $\sqrt{81}= 9(m)$
Bài tập 7 trang 34
Áp dụng công thức: $S=3,14 . R^2 \Rightarrow R=\sqrt{\frac{S}{3,14}}$
Bán kính của hình tròn là: $R=\sqrt{\frac{S}{3,14}}=\sqrt{\frac{9869}{3,14}} \approx 56,1$ (m)$.
Bài tập 8 trang 34
$12 ; \quad \frac{2}{3} ; \quad 3,(14) ; \quad 0,123 ; \quad \sqrt{3}$
Số hữu tỉ gồm các số thập phân hữu hạn và vô hạn tuần hoàn.
Số vô tỉ gồm các số thập phân vô hạn không tuần hoàn.
Ta có $\sqrt{3}=1,732 \ldots$ nên là số thập phân vô hạn không tuần hoàn nên $\sqrt{3}$ là số vô tỉ.
Các số hữu tỉ là: $12 ; \frac{2}{3} ; 3,(14) ; 0,123$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 1 chương 2 – Số thực trang 30, 31, 32, 33, 34 Toán 7 Chân trời sáng tạo tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




