Giải SGK Bài 4 Chương 7 trang 37, 38, 39, 40 Toán 7 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các hoạt động khám phá, thực hành và vận dụng trong bài Phép nhân và phép chia đa thức một biến. Các bài tập sau đây thuộc bài 4 chương VII – Biểu thức đại số trang 37, 38, 39, 40 Toán 7 Chân trời sáng tạo tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời hoạt động khám phá và thực hành trang 37, 38, 39 Toán 7 Chân trời sáng tạo tập 2
Dưới đây là phương pháp và bài giải chi tiết cho các hoạt động khám phá, thực hành và vận dụng ở các trang 37, 38, 39 trong bài Phép nhân và phép chia đa thức một biến. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động khám phá 1 trang 37
Sử dụng tính chất nhân phân phối
Lời giải chi tiết:
$x .(2 x+3)$
$=x .2 x+3 . x$
$=2 x^2+3 x$
Hoạt động khám phá 2 trang 38
– Nhân chia đa thức bằng phương pháp phân phối
$ (3 x+1)t(x^2-2 x+1) $
$ =3 x(x^2-2 x+1)+1(x^2-2 x+1) $
$ =3 x^3-6 x^2+3 x+x^2-2 x+1 $
$ =3 x^3-5 x^2+x+1 $
$ \text { Vì }(3 x+1)(x^2-2 x+1)=3 x^3-5 x^2+x+1 $
$ \Rightarrow (3 x^3-5 x^2+x+1):(3 x+1)=x^2-2 x+1$
Thực hành 1 trang 37
Ta dùng tính chất phân phối để thực hiện phép tính
$ (4 x-3)\left(2 x^2+5 x-6\right) $
$ =4 x .2 x^2+4 x .5 x-6.4 x-3.2 x^2-3.5 x+18 $
$ =8 x^3+20 x^2-6 x^2-24 x-15 x+18 $
$ =8 x^3+14 x^2-39 x+18 $
Thực hành 2 trang 38
– Sử dụng công thức chia đa thức một biến
$ \left(6 x^2+4 x\right): 2 x=\left(6 x^2: 2 x\right)+(4 x: 2 x) $
$ =3 x+2$
Thực hành 3 trang 39
Ta sử dụng qui tắc chia 2 đa thức
$\left(x^2+2 x+9\right):(x+2)=\frac{x^2+5 x+9}{3 x+6}=x+3+\frac{3}{x+2} \text { ta có : }$
$$\begin{array}{r|r}x^2+5 x+9 & \underline {x+2} \\ \underline {-x^2+2 x} & x+3 \\ 3 x+9 & \\\underline{-3 x+6} & \\ 3 &\end{array}$$
$$\text { Vậy }=x+3+\frac{3}{x+2}$$
Thực hành 4 trang 40
Sử dụng tính chất phân phối và giao hoán của phép nhân đa thức.
$ \frac{1}{5}\left(x^2+1\right) . 5 $
$ =\frac{1}{5} . 5 .\left(x^2+1\right) $
$ =\left(\frac{1}{5} .5\right) .x^2+1 $
$ =1 .\left(x^2+1\right) $
$ =x^2+1$
Vận dụng 1 trang 37
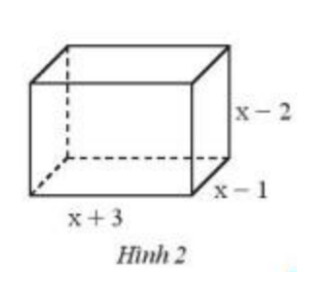
Thể tích hình hộp chữ nhật = chiều dài . chiều rộng . chiều cao
Thể tích hình hộp chữ nhật là :
$ (x+3) .(x-1) .(x-2) $
$ =[(x+3) .(x-1)] .(x-2) $
$ =(x . x-1 . x+3. x-3 . 1)(x-2) $
$ =\left(x^2+2 x-3\right)(x-2) $
$ =x^2 . x-2 . x^2+2 x . x-2 x . 2-3 . x+3 2 $
$ =x^3-7 x+6$
Vận dụng 2 trang 39
– Ta chia lần lượt theo công thức đã cho, phải thu gọn các đa thức trong phép chia và xếp thứ tự lũy thừa giảm dần của biến
$ \frac{9 x^2+5 x+x}{3 x}=\frac{9 x^2+6 x}{3 x}=\frac{9 x^2}{3 x}+\frac{6 x}{3 x}=3 x+2 $
$ \frac{2 x^2-3 x-2}{2-x}=\frac{2 x^2-3 x-2}{-x+2}=-2 x-1$
Vận dụng 3 trang 39
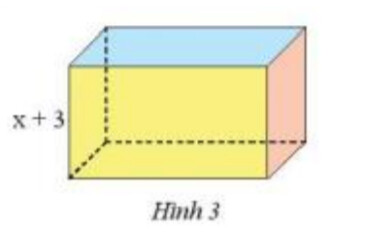
– Ta tính diện tích đáy của hình hộp chữ nhật có chiều cao là $(x+3) \mathrm{cm}$
– Ta sử dụng công thức V = S.h để tìm ra diện tích đáy
$\Rightarrow(x^3+8 x^2+19 x+12):(x+3)=$ diện tích đáy
Vậy diện tích đáy $ = x^2+5 x+4 \mathrm{~cm}^2$
Giải bài tập SGK Bài 4 Chương 7 trang 40 Toán 7 Chân trời sáng tạo tập 2
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Phép nhân và phép chia đa thức một biến trang 40 sách Toán 7 chân trời sáng tạo tập 2 dưới đây nhé!
Bài tập 1 trang 40
a) $(4 x-3)(x+2)$
b) $(5 x+2)(-x^2+3 x+1)$
c) $(2 x^2-7 x+4)(-3 x^2+6 x+5)$
– Áp dụng các qui tắc nhân đa thức (phân phối)
a) $(4 x-3)(x+2)=4 x(x+2)-3(x+2) $
$ =4 x^2+8 x-3 x-6 $
$ = 4 x^2+5 x-6 $
b) $ (5 x+2)(-x^2+3 x+1) $
$= 5 x(-x^2+3 x+1)+2(-x^2+3 x+1) $
$= -5 x^3+15 x^2+5 x-2 x^2+6 x+2 $
$= -5 x^3+13 x^2+11 x+2 $
c) $ (2 x^2-7 x+4)$ $(-3 x^2+6 x+5) $
$= 2 x^2(-3 x^2+6 x+5)-7 x(-3 x^2+6 x+5)+4(-3 x^2+6 x+5) $
$= 2 x^2(-3 x^2)+2 x^2 . 6 x+2 x^2 .5+7 x .3 x^2-7 x .6 x-7 x .5+4(-3 x^2)+4.6 x+4.5 $
$= -6 x^4+33 x^3-44 x^2-11 x+20$
Bài tập 2 trang 40
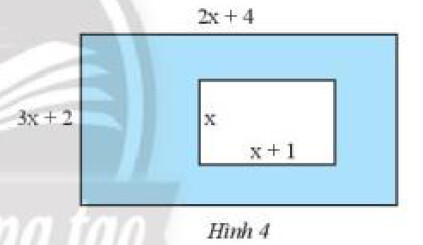
– Ta tính diện tích hình chữ nhật lớn
– Ta tính diện tích hình chữ nhật nhỏ
– Lấy diện tích hình chữ nhật lớn trừ diện tích hình chữ nhật nhỏ thì được diện tích cần tìm.
Diện tích hình chữ nhật nhỏ là : $x(x+1)=x^2+x$
Diện tích phần cần tìm là : $6 x^2+16 x+8-x^2-x=5 x^2+15 x+8$
Bài tập 3 trang 40
а) $(8 x^6-4 x^5+12 x^4-20 x^3): 4 x^3$
b) $(2 x^2-5 x+3):(2 x-3)$
Thực hiện phép nhân chia đa thức bằng cách đặt tính.
Chú ý: Sắp xếp thứ tự đa thức theo giảm dần của lũy thừa
a)$(8 x^6-4 x^5+12 x^4-20 x^3): 4 x^3 $
$=(8 x^6: 4 x^3)-(4 x^5: 4 x^3)+(12 x^4: 4 x^3)-(20 x^3: 4 x^3)$
$ =2 x^2-x^2+3 x-5$
b)
$\begin{array}{r|r}2 x^2-5 x+3 & \underline {2 x-3 }\\\underline{2 x^2-3 x} & x-1 \\-2 x+3 & \\\underline{-2 x+3} & \\ 0 &\end{array}$
Vậy $(2 x^2-5 x+3):(2 x-3)=x-1$
Bài tập 4 trang 40
a) $\left(4 x^2-5\right):(x-2)$
b) $(3 x^3-7 x+2):(2 x^2-3)$
Sử dụng các qui tắc đã học để chia đa thức
Nên sắp xếp đa thức theo lũy thừa giảm dần để dễ thực hiện tính
a) $(4 x^2-5):(x-2)=\frac{4 x^2-5}{x-2}=4 x+8+\frac{11}{x-2}$
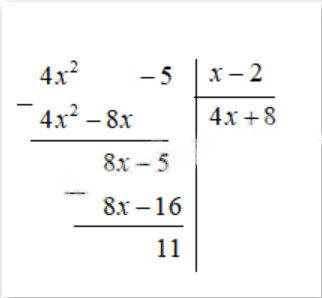
Vậy $(4 x^2-5):(x-2)=4 x+8+\frac{11}{x-2}$
b) $(3 x^3-7 x+2):(2 x^2-3)=\frac{3 x^3-7 x+2}{2 x^2-3}$
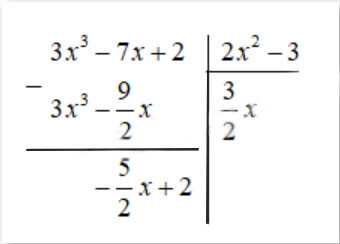
Vậy $(3 x^3-7 x+2):(2 x^2-3)=\frac{3}{2} x-\frac{\frac{5}{2} x+2}{2 x^2-3}$
Bài tập 5 trang 40
Sử dụng công thức tính diện tích hình chữ nhật
Áp dụng qui tắc chia đa thức và sắp xếp đa thức theo thứ tự giảm dần của lũy thừa
Diện tích hình chữ nhật = chiều dài . chiều rộng
$\Rightarrow(4 y^2+4 y-3):(2 y-1)=\frac{4 y^2+4 y-3}{2 y-1}$
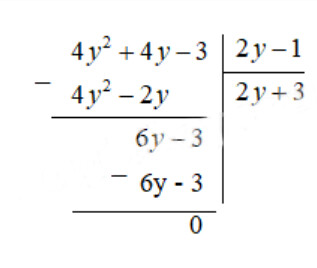
Vậy chiều dài hình chữ nhật là : $2 \mathrm{y}+3 \mathrm{~cm}$
Bài tập 6 trang 40
Sử dụng công thức tính thể tích hình hộp chữ nhật V=S.h
Áp dụng qui tắc chia 2 đa thức
Ta có thể tích hình hộp chữ nhật bằng tích chiều cao và diện tích đáy. Nên chiều rộng của hình chữ nhật = thể tích : (chiều cao . chiều dài)
Diện tích đáy là $(x+5)(x+1)=x^2+6 x+5$
Thay các số ở đề bài cho vào công thức trên ta được :
$=\frac{3 x^3+8 x^2-45 x-50}{(x+5)(x+1)=x^2+6 x+5}=\frac{3 x^3+8 x^2-45 x-50}{x^2+6 x+5}$
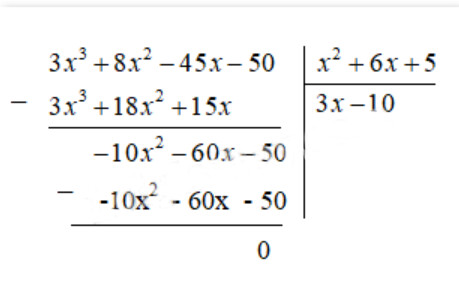
Vậy chiều dài hình hộp chữ nhật là $3x-10cm$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 4 chương VII – Biểu thức đại số trang 37, 38, 39, 40 Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




