SGK Toán 7 – Chân Trời Sáng Tạo
Giải SGK bài tập cuối chương 7 Toán 7 Chân trời sáng tạo Tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những bài tập tự luận trong bài tập ôn tập cuối chương 7. Đây là Bài tập cuối chương 7 trang 42 sách Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Bài 1 trang 42
Cho $\mathrm{A}=\mathrm{x}^2 \mathrm{y}+2 \mathrm{xy}-3 \mathrm{y}^2+4$. Tính giá trị của biểu thức $\mathrm{A}$ khi $\mathrm{x}=-2, \mathrm{y}=3$.
Phương pháp giải:
Ta thay các $x, y$ đề bài cho trước vào biểu thức rồi tính
Ta thay các $x, y$ đề bài cho trước vào biểu thức rồi tính
Lời giải chi tiết:
$$A=x^2 y+2 x y-3 y^2+4$$
Thay các $x=-2$ và $y=3$ vào công thức ta có :
$$\begin{aligned}& A=(-2)^2 .3+2(-2) .3-3.3^2+4 \\& =4.3-12-27+4 \\& =-23\end{aligned}$$
$$A=x^2 y+2 x y-3 y^2+4$$
Thay các $x=-2$ và $y=3$ vào công thức ta có :
$$\begin{aligned}& A=(-2)^2 .3+2(-2) .3-3.3^2+4 \\& =4.3-12-27+4 \\& =-23\end{aligned}$$
Bài 2 trang 42
Trong các biểu thức sau, biểu thức nào là đơn thức một biến?
a) $2 y ;$
b) $3 x+5$
c) $8$
d) $21 t^{12}$.
a) $2 y ;$
b) $3 x+5$
c) $8$
d) $21 t^{12}$.
Phương pháp giải:
Định nghĩa đơn thức một biến.
Định nghĩa đơn thức một biến.
Lời giải chi tiết:
Các đa thức 1 biến là $a, c, d$
Các đa thức 1 biến là $a, c, d$
Bài 3 trang 42
Trong các biểu thức sau, biểu thức nào là đa thức một biến?
$$\begin{array}{ll}3+6 y ; & 7 \mathrm{x}^2+2 \mathrm{x}-4 \mathrm{x}^4+1 \\\frac{2}{\mathrm{x}+1} ; & \frac{1}{3} \mathrm{x}-5\end{array}$$
$$\begin{array}{ll}3+6 y ; & 7 \mathrm{x}^2+2 \mathrm{x}-4 \mathrm{x}^4+1 \\\frac{2}{\mathrm{x}+1} ; & \frac{1}{3} \mathrm{x}-5\end{array}$$
Phương pháp giải:
Dựa vào định nghĩa của đa thức 1 biến
Dựa vào định nghĩa của đa thức 1 biến
Lời giải chi tiết:
Các đa thức 1 biến là :
$$3+6 y ; 7 x^2+2 x-4 x^4+1 ; \frac{1}{3} x-5$$
Các đa thức 1 biến là :
$$3+6 y ; 7 x^2+2 x-4 x^4+1 ; \frac{1}{3} x-5$$
Bài 4 trang 42
Hãy viết một đa thức một biến bậc ba có 3 số hạng.
Phương pháp giải:
Sử dụng các định nghĩa về bậc trong đa thức 1 biến
Sử dụng các định nghĩa về bậc trong đa thức 1 biến
Lời giải chi tiết:
$$x^3+2 x-1$$
Chú ý : Có nhiều cách khác nhau để viết đa thức nhưng trong bài này các số hạng trong đa thức luôn luôn là 3
$$x^3+2 x-1$$
Chú ý : Có nhiều cách khác nhau để viết đa thức nhưng trong bài này các số hạng trong đa thức luôn luôn là 3
Bài 5 trang 42
Hãy cho biết bậc của các đa thức sau:
$$\begin{aligned}& \mathrm{A}=3 \mathrm{x}-4 \mathrm{x}^2+1 \\& \mathrm{~B}=7 \\& \mathrm{M}=\mathrm{x}-7 \mathrm{x}^3+10 \mathrm{x}^4+2\end{aligned}$$
$$\begin{aligned}& \mathrm{A}=3 \mathrm{x}-4 \mathrm{x}^2+1 \\& \mathrm{~B}=7 \\& \mathrm{M}=\mathrm{x}-7 \mathrm{x}^3+10 \mathrm{x}^4+2\end{aligned}$$
Phương pháp giải:
Dựa vào các định nghĩa về bậc trong đa thức
Dựa vào các định nghĩa về bậc trong đa thức
Lời giải chi tiết:
$A$ có bậc là $2$
$B$ có bậc là $0$
$M$ có bậc là $4$
$A$ có bậc là $2$
$B$ có bậc là $0$
$M$ có bậc là $4$
Bài 6 trang 42
Cho đa thức $\mathrm{P}(\mathrm{x})=\mathrm{x}^3+27$. Tìm nghiệm của $\mathrm{P}(\mathrm{x})$ trong tập hợp $\{0 ; 3 ;-3\}$.
Phương pháp giải:
Ta xét $\mathrm{P}(\mathrm{x})=0$ rồi tìm $\mathrm{x}$. Giá trị $\mathrm{x}$ tìm được là nghiệm của đa thức
Ta xét $\mathrm{P}(\mathrm{x})=0$ rồi tìm $\mathrm{x}$. Giá trị $\mathrm{x}$ tìm được là nghiệm của đa thức
Lời giải chi tiết:
Xét $\mathrm{P}(\mathrm{X})=x^3+27=0$
$\Leftrightarrow x^3=-27$
$\Leftrightarrow x^3=-27=(-3)^3$
$\Rightarrow x=-3$
Vì $-3 \in\{0 ; 3 ;-3\}$ nên $-3$ là 1 nghiệm
Xét $\mathrm{P}(\mathrm{X})=x^3+27=0$
$\Leftrightarrow x^3=-27$
$\Leftrightarrow x^3=-27=(-3)^3$
$\Rightarrow x=-3$
Vì $-3 \in\{0 ; 3 ;-3\}$ nên $-3$ là 1 nghiệm
Bài 7 trang 42
Tam giác trong Hình 1 có chu vi bằng $(25y – 8) cm$. Tìm cạnh chưa biết trong tam giác đó.
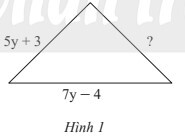
Phương pháp giải:
– Ta tính cạnh còn lại bằng cách lấy chu vi trừ đi 2 cạnh còn lại đã biết
– Sử dụng qui tắc cộng, trừ đa thức
– Ta tính cạnh còn lại bằng cách lấy chu vi trừ đi 2 cạnh còn lại đã biết
– Sử dụng qui tắc cộng, trừ đa thức
Lời giải chi tiết:
Cạnh còn lại cần tìm của tam giác là:
25 y-8-(5 y+3)-(7 y-4) \\\\ =25 y-8-5 y-3-7 y+4 \\\\ =(25 y-5 y-7 y)+(-8-3+4) \\\\ =13 y-7(\mathrm{~cm})
Cạnh còn lại cần tìm của tam giác là:
25 y-8-(5 y+3)-(7 y-4) \\\\ =25 y-8-5 y-3-7 y+4 \\\\ =(25 y-5 y-7 y)+(-8-3+4) \\\\ =13 y-7(\mathrm{~cm})
Bài 8 trang 42
Cho đa thức
$$M(x)=2 x^4-5 x^3+7 x^2+3 x$$
Tìm các đa thức $\mathrm{N}(\mathrm{x}), \mathrm{Q}(\mathrm{x})$ sao cho: $\mathrm{N}(\mathrm{x})-\mathrm{M}(\mathrm{x})=-4 \mathrm{x}^4-2 \mathrm{x}^3+6 \mathrm{x}^2+7$ và $\mathrm{Q}(\mathrm{x})+\mathrm{M}(\mathrm{x})=6 \mathrm{x}^5-\mathrm{x}^4+3 \mathrm{x}^2-2$.
$$M(x)=2 x^4-5 x^3+7 x^2+3 x$$
Tìm các đa thức $\mathrm{N}(\mathrm{x}), \mathrm{Q}(\mathrm{x})$ sao cho: $\mathrm{N}(\mathrm{x})-\mathrm{M}(\mathrm{x})=-4 \mathrm{x}^4-2 \mathrm{x}^3+6 \mathrm{x}^2+7$ và $\mathrm{Q}(\mathrm{x})+\mathrm{M}(\mathrm{x})=6 \mathrm{x}^5-\mathrm{x}^4+3 \mathrm{x}^2-2$.
Phương pháp giải:
Áp dụng qui tắc cộng trừ các đa thức 1 biến
Áp dụng qui tắc cộng trừ các đa thức 1 biến
Lời giải chi tiết:
Theo đề bài ta có $M(x)=2 x^4-5 x^3+7 x^2+3 x$
M(x)+Q(x)=6 x^5-x^4+3 x^2-2 \\\\ \Rightarrow Q(x)=(6 x^5-x^4+3 x^2-2)-(2 x^4-5 x^3+7 x^2+3 x) \\\\ \Rightarrow Q(x)=6 x^5-x^4+3 x^2-2-2 x^4+5 x^3-7 x^2-3 x \\\\ \Rightarrow Q(x)=6 x^5-3 x^4+5 x^3-4 x^2-3 x-2
Theo đề bài ta có :
N(x)-M(x)=-4 x^4-2 x^3+6 x^2+7 \\\\ \Rightarrow N(x)=-4 x^4-2 x^3+6 x^2+7+2 x^4-5 x^3+7 x^2+3 x \\\\ \Rightarrow N(x)=-2 x^4-7 x^3+13 x^2+3 x+7
Theo đề bài ta có $M(x)=2 x^4-5 x^3+7 x^2+3 x$
M(x)+Q(x)=6 x^5-x^4+3 x^2-2 \\\\ \Rightarrow Q(x)=(6 x^5-x^4+3 x^2-2)-(2 x^4-5 x^3+7 x^2+3 x) \\\\ \Rightarrow Q(x)=6 x^5-x^4+3 x^2-2-2 x^4+5 x^3-7 x^2-3 x \\\\ \Rightarrow Q(x)=6 x^5-3 x^4+5 x^3-4 x^2-3 x-2
Theo đề bài ta có :
N(x)-M(x)=-4 x^4-2 x^3+6 x^2+7 \\\\ \Rightarrow N(x)=-4 x^4-2 x^3+6 x^2+7+2 x^4-5 x^3+7 x^2+3 x \\\\ \Rightarrow N(x)=-2 x^4-7 x^3+13 x^2+3 x+7
Bài 9 trang 42
Thực hiện phép nhân.
a) $(3 x-2)(4 x+5)$
b) $\left(x^2-5 x+4\right)(6 x+1)$.
a) $(3 x-2)(4 x+5)$
b) $\left(x^2-5 x+4\right)(6 x+1)$.
Phương pháp giải:
Áp dụng qui tắc nhân 2 đa thức 1 biến
Áp dụng qui tắc nhân 2 đa thức 1 biến
Lời giải chi tiết:
a) (3 x-2)(4 x+5) \\\\ = 3 x(4 x+5)-2(4 x+5) \\\\ = 3 x.4 x+5.3 x-2.4 x-2.5 \\\\ = 12 x^2+7 x-10
b) (x^2-5 x+4)(6 x+1) \\\\ = x^2(6 x+1)-5 x(6 x+1)+4(6 x+1) \\\\ = x^2 .6 x+1 . x^2-5 x .6 x-5 x .1+4.6 x+4.1 \\\\ = 6 x^3-29 x^2+19 x+4
a) (3 x-2)(4 x+5) \\\\ = 3 x(4 x+5)-2(4 x+5) \\\\ = 3 x.4 x+5.3 x-2.4 x-2.5 \\\\ = 12 x^2+7 x-10
b) (x^2-5 x+4)(6 x+1) \\\\ = x^2(6 x+1)-5 x(6 x+1)+4(6 x+1) \\\\ = x^2 .6 x+1 . x^2-5 x .6 x-5 x .1+4.6 x+4.1 \\\\ = 6 x^3-29 x^2+19 x+4
Bài 10 trang 42
Thực hiện phép chia.
a) $\left(45 x^5-5 x^4+10 x^2\right): 5 x^2$;
b) $\left(9 t^2-3 t^4+27 t^5\right): 3 t$.
a) $\left(45 x^5-5 x^4+10 x^2\right): 5 x^2$;
b) $\left(9 t^2-3 t^4+27 t^5\right): 3 t$.
Lời giải chi tiết:
a) (45 x^5-5 x^4+10 x^2): 5 x^2 \\\\ =(45 x^5: 5 x^2)+(-5 x^4: 5 x^2)+(10 x^2: 5 x^2) \\\\ =9 x^3-x^2+2
b) (9 t^2-3 t^4+27 t^5): 3 t \\\\ =(9 t^2: 3 t)+(-3 t^4: 3 t)+(27 t^5: 3 t) \\\\ =3 t-t^3+9 t^4
a) (45 x^5-5 x^4+10 x^2): 5 x^2 \\\\ =(45 x^5: 5 x^2)+(-5 x^4: 5 x^2)+(10 x^2: 5 x^2) \\\\ =9 x^3-x^2+2
b) (9 t^2-3 t^4+27 t^5): 3 t \\\\ =(9 t^2: 3 t)+(-3 t^4: 3 t)+(27 t^5: 3 t) \\\\ =3 t-t^3+9 t^4
Bài 11 trang 42
Thực hiện phép chia.
a) $\left(2 y^4-13 y^3+15 y^2+11 y-3\right):\left(y^2-4 y-3\right)$;
b) $\left(5 x^3-3 x^2+10\right):\left(x^2+1\right)$.
a) $\left(2 y^4-13 y^3+15 y^2+11 y-3\right):\left(y^2-4 y-3\right)$;
b) $\left(5 x^3-3 x^2+10\right):\left(x^2+1\right)$.
Phương pháp giải:
Đặt tính và chia 2 đa thức
Ta sắp xếp các đa thức theo thứ tự giảm dần của lũy thừa để dễ thực hiện phép tính hơn
Đặt tính và chia 2 đa thức
Ta sắp xếp các đa thức theo thứ tự giảm dần của lũy thừa để dễ thực hiện phép tính hơn
Lời giải chi tiết:
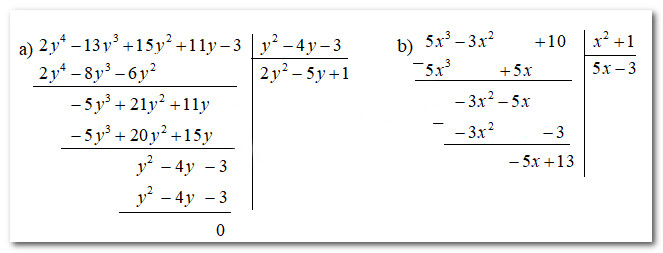
a) $\left(2 y^4-13 y^3+15 y^2+11 y-3\right):\left(y^2-4 y-3\right)=2 y^2-5 y+1$
b) $\left(5 x^3-3 x^2+10\right):\left(x^2+1\right)=5 x-3+\frac{-5 x+13}{x^2+1}$
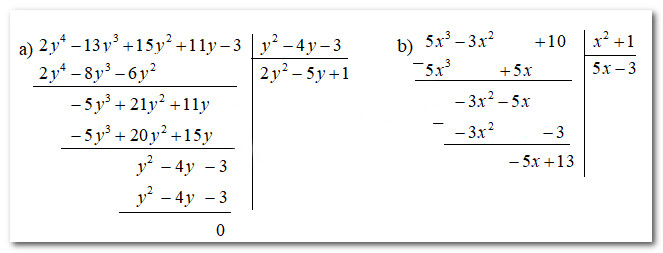
a) $\left(2 y^4-13 y^3+15 y^2+11 y-3\right):\left(y^2-4 y-3\right)=2 y^2-5 y+1$
b) $\left(5 x^3-3 x^2+10\right):\left(x^2+1\right)=5 x-3+\frac{-5 x+13}{x^2+1}$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK Bài tập cuối chương 7 Toán 7 Chân trời sáng tạo tập 2 ở các trang 42. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!
Bài viết khác liên quan đến Lớp 7 – Toán – Ôn tập chương biểu thức đại số
- Giải SGK Bài tập cuối chương 6 trang 68, 69 Toán 7 Cánh diều tập 2
- Giải SGK bài tập cuối chương VI Toán 7 Chân trời sáng tạo Tập 2
- Giải bài tập cuối chương 7 trang 46 SGK Toán 7 Kết nối tri thức Tập 2
- Giải Luyện tập chung Chương 7 trang 44, 45 SGK Toán 7 Kết nối tri thức Tập 2
- Giải Luyện tập chung trang 34, 35 SGK Toán 7 Kết nối tri thức Tập 2




