Giải SGK Bài 8 Chương 8 trang 77, 78 Toán 7 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khám phá, thực hành, vận dụng trong bài Tính chất ba đường cao của tam giác. Các bài tập sau đây thuộc bài 8 chương VIII – Tam giác trang 77, 78 Toán 7 Chân trời sáng tạo tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời hoạt động khám phá, thực hành Bài 8 Chương 8 trang 77
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần vận dụng ở các trang 77, 78 trong bài Tính chất ba đường cao của tam giác. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động khám phá 1 trang 77
– Ta dùng êke với cạnh góc vuông đi qua đỉnh $B$
– Cạnh góc vuông còn lại của êke nằm trùng với $A C$
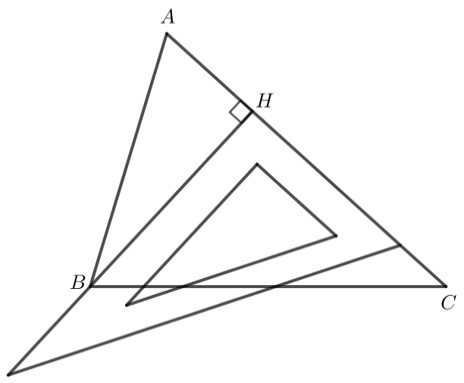
– Ta dùng êke với cạnh góc vuông đi qua đỉnh $B$
– Cạnh góc vuông còn lại của êke nằm trùng với $A C$
Hoạt động khám phá 2 trang 77
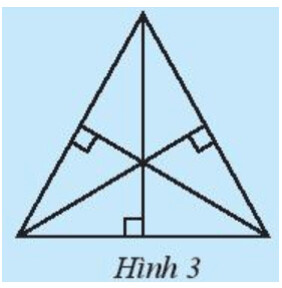
– Ta sử dụng êke vẽ 3 đường cao của tam giác
– Sau đó nhận xét về các giao điểm của những đường cao ấy
Nhận xét: Các đường cao cùng đi qua 1 điểm
Thực hành 1 trang 77
– Ta sử dụng thước êke để vẽ đường cao từ các đỉnh
– Ta đặt 1 cạnh góc vuông của êke đi qua 1 đỉnh của tam giác và cạnh góc vuông còn lại của êke trùng với cạnh đối diện với đỉnh đang vẽ .
– Sau đó ta vẽ đường cao của tam giác bằng cạnh góc vuông đi qua đỉnh cần vẽ
Thực hành 2 trang 78
– Ta sử dụng định lí 3 đường cao của một tam giác cùng đi qua 1 điểm
Theo giả thiết ta có: $LP$ và $MQ$ là 2 đường cao của tam giác
Chúng cắt nhau tại $S$
Theo định lí 3 đường cao trong 1 tam giác cùng đi qua 1 điểm
\Rightarrow Đường cao từ đỉnh $N$ cũng đi qua $S$
\Rightarrow $NS$ là đường cao của tam giác $MNL$
\Rightarrow $NS$ vuông góc với $ML$ tại $G$ (là chân đường cao)
Vận dụng 1 trang 77
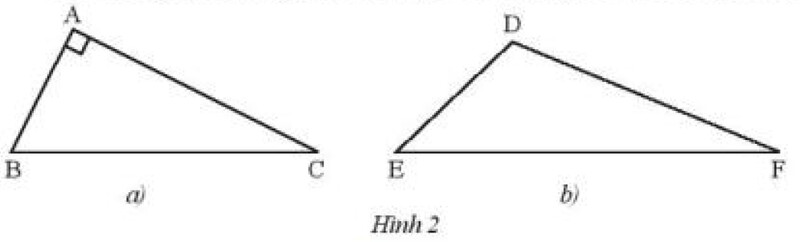
Vẽ đường cao xuất phát từ đỉnh $\mathrm{F}$ của tam giác tù $\mathrm{DEF}$ (Hình $2 \mathrm{~b}$
– Ta sử dụng thước êke để vẽ đường cao từ các đỉnh
– Ta đặt 1 cạnh góc vuông của êke đi qua 1 đỉnh của tam giác và cạnh góc vuông còn lại của êke trùng với cạnh đối diện với đỉnh đang vẽ
– Sau đó ta vẽ đường cao của tam giác bằng cạnh góc vuông đi qua đỉnh cần vẽ
a) Ta thấy ở tam giác $A B C$ vuông tại $A$ thì $B A$ chính là đường cao từ đỉnh $B$ của tam giác vuông $A B C$
b) Ta thấy đường cao tam giác tù $\mathrm{DEF}$ xuất phát từ đỉnh $\mathrm{F}$ sẽ nằm ngoài tam giác $\mathrm{DEF}$ và chân đường cao nằm trên đoạn kéo dài của đoạn $\mathrm{ED}$.
Vận dụng 2 trang 78
– Từ các đỉnh ta vẽ các đường cao của tam giác chúng giao nhau ở đâu thì đó là trực tâm
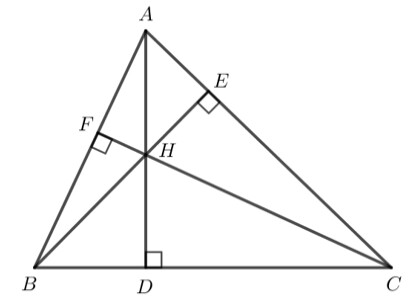
+) Xét tam giác $\mathrm{HBC}$ ta có :
$\mathrm{HD}$ vuông góc với $\mathrm{BC} \Rightarrow \mathrm{HD}$ là đường cao tam giác $\mathrm{HBC}$
$BF$ vuông góc với $\mathrm{HC}$ tại $\mathrm{F}$ (kéo dài $\mathrm{HC}$ ) $\Rightarrow \mathrm{BF}$ là đường cao của tam giác $\mathrm{HBC}$
$CE$ vuông góc với $\mathrm{HB}$ tại $\mathrm{E}$ (kéo dài $\mathrm{HB}$ ) $\Rightarrow \mathrm{CE}$ là đường cao của tam giác $\mathrm{HBC}$
Ta kéo dài $\mathrm{HD}, \mathrm{BF}, \mathrm{CE}$ sẽ cắt nhau tại $\mathrm{A}$
$\Rightarrow \mathrm{A}$ là trực tâm tam giác $\mathrm{HBC}$
+) Xét tam giác $HAB$ ta có :
$HF$ vuông góc với $A B \Rightarrow H F$ là đường cao tam giác $H A B$
$BH$ vuông góc với $A E$ tại $E$ (kéo dài $\mathrm{HB}$ ) $\Rightarrow A E$ là đường cao của tam giác $H A B$
$B D$ vuông góc với $A H$ tại $D$ (kéo dài $A H$ ) $\Rightarrow B D$ là đường cao của tam giác $\mathrm{HAB}$
Ta kéo dài $\mathrm{HF}, \mathrm{BD}$, $\mathrm{AE}$ sẽ cắt nhau tại $\mathrm{C}$
$\Rightarrow$ $C$ là trực tâm tam giác $H A B$
+) Xét tam giác $HAC$ ta có :
$\mathrm{HE}$ vuông góc với $\mathrm{AC} \Rightarrow \mathrm{HE}$ là đường cao tam giác $\mathrm{HAC}$
$A F$ vuông góc với $\mathrm{HC}$ tại $\mathrm{F}$ (kéo dài $\mathrm{HC}$ ) $\Rightarrow \mathrm{AF}$ là đường cao của tam giác $\mathrm{HAC}$
$C D$ vuông góc với $A H$ tại $D$ (kéo dài $A H$ ) $\Rightarrow C D$ là đường cao của tam giác $\mathrm{HAC}$
Ta kéo dài $\mathrm{CD}, \mathrm{HE}$, $\mathrm{AF}$ sẽ cắt nhau tại $\mathrm{B}$
$\Rightarrow \mathrm{B}$ là trực tâm tam giác $\mathrm{HAC}$.
Giải bài tập SGK Bài 8 Chương 8 trang 78 Toán 7 Chân trời sáng tạo tập 2
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Tính chất ba đường cao của tam giác trang 78 sách Toán 7 chân trời sáng tạo tập 2 dưới đây nhé!
Bài tập 1 trang 78
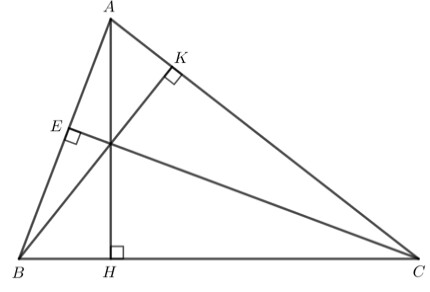
Ta chứng minh $\mathrm{H}$ là trực tâm của tam giác $NBC$
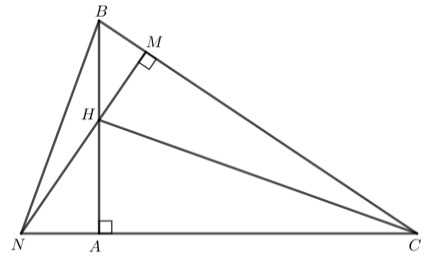
Vì tam giác $ABC$ vuông tại $A$ theo giả thiết nên $BA$ vuông góc với $AC$
Vì $HM$ cắt $AC$ tại $N$ mà $HM$ vuông góc với $BC$ (giả thiết)
$\Rightarrow NM$ vuông góc với $BC$ tại $M$
Xét tam giác $NBC$ có $NM$ và $BA$ là 2 đường cao
Mà $M N$ cắt $A B$ tại $H$ nên $H$ là trực tâm của tam giác $NBC$
$\Rightarrow \mathrm{CH}$ đường cao của tam giác $NBC$ (3 đường cao của tam giác đi qua 1 điểm)
$\Rightarrow \mathrm{CH}$ vuông góc với $NB$
Bài tập 2 trang 78
– Ta chứng minh $H$ là trực tâm của tam giác $AMC$
– Từ đó ta chứng minh $MH$ vuông góc với $BC$
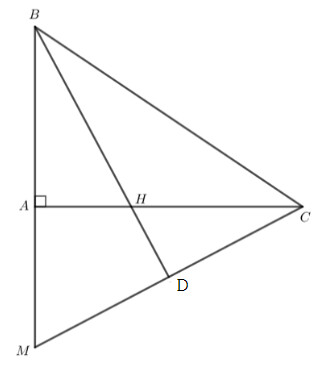
Gọi $D$ giao điểm của tia phân giác của góc $B$ và $M C$
Xét tam giác $\mathrm{BDM}$ và tam giác $\mathrm{BDC}$ có:
$BD$ chung
$\widehat{M B D}=\widehat{C B D}(\mathrm{BD}$ là phân giác của góc $\mathrm{B})$
$\mathrm{BM}=\mathrm{BC}$ (giả thiết)
($\Rightarrow \Delta B D M=\Delta B D C$) (c.g.c)
$\Rightarrow \widehat{B D M}=\widehat{B D C}$ (2 góc tương ứng)
Mà 2 góc ở vị trí kề bù $\Rightarrow \widehat{B D M}=\widehat{B D C}=90^{\circ} \Rightarrow B D \perp C M$
Mà $\mathrm{AC}$ cắt $\mathrm{BD}$ tại $\mathrm{H} \Rightarrow \mathrm{H}$ là trực tâm tam giác $\mathrm{BMC}$
$\Rightarrow \mathrm{MH}$ là đường cao của tam giác $BMC$ (định lí 3 đường cao đi qua trực tâm tam giác)
$\Rightarrow \mathrm{MH}$ vuông góc với $B C$
Bài tập 3 trang 78
a) $DE$ vuông góc với $BC$
b) $BE$ vuông góc với $DC$
– Ta chứng minh vuông góc qua các tam giác vuông cân
– Ta chứng minh $E$ là trực tâm của tam giác $B C D$
– Từ đó ta chứng minh $D E$ vuông góc với $B C$ và $B E$ vuông góc $D C$
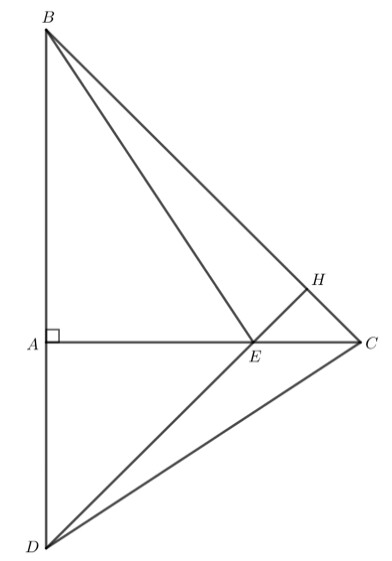
a) Vì tam giác $A B C$ vuông cân tại $A$
$\Rightarrow \widehat{B}=\widehat{C}=45^{\circ}$ (2 góc ở đáy bằng nhau)
Xét tam giác $AED$ có :
$A E=A D$
$A C$ vuông góc với $A B$
$\Rightarrow$ Tam giác $A E D$ vuông cân tại $A$
$\Rightarrow \widehat{A D E}=\widehat{A E D}=45^{\circ}$
Mà $\widehat{A E D} ; \widehat{C E H}$ là 2 góc đối đỉnh $\Rightarrow \widehat{A E D}=\widehat{C E H}=45^{\circ}$
Xét tam giác $CEH$ áp dụng định lí tổng 3 góc trong tam giác ta có :
$ \Rightarrow \widehat{H}+\widehat{C}+\widehat{E}=180^{\circ} $
$ \Rightarrow \widehat{H}=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$
$ \Rightarrow E H \perp B C \Rightarrow D E \perp B C $
b) Vì $DE$ vuông góc với $\mathrm{BC} \Rightarrow \mathrm{DE}$ là đường cao của tam giác $\mathrm{BCD}$
Vì $A C$ cắt $D E$ tại $E$ nên $E$ là trực tâm tam giác $B C D$ (Do $A C$ cũng là đường cao của tam giác $B C D$ )
$\Rightarrow B E$ cùng là đường cao của tam giác $B C D$ (định lí 3 đường cao trong tam giác đi qua trực tâm)
$\Rightarrow B E$ vuông góc với $DC$
Bài tập 4 trang 78
– Ta chứng tam giác $\mathrm{BFC}=$ tam giác $\mathrm{BEC}$
– Từ đó suy ra góc $\mathrm{B}=$ góc $\mathrm{C}$
– Chứng minh tương tự suy ra được góc $\mathrm{A}=$ góc $\mathrm{B}=$ góc $\mathrm{C}$
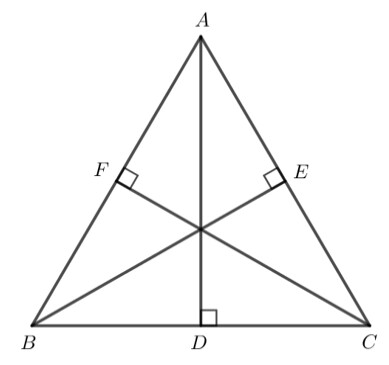
Xét tam giác $BFC$ và tam giác $BEC$ có :
$\mathrm{BC}$ chung
$\mathrm{FC}=\mathrm{BE}$
$\widehat{B F C}=\widehat{B E C}=90^{\circ}$
( cạnh huyền – cạnh góc vuông)
$\Rightarrow \widehat{C}=\widehat{B}$ ( 2 góc tương ứng ) (1)
Xét tam giác $CFA$ và tam giác $A D C$ ta có :
$\mathrm{CF}=\mathrm{AD}$
$A C$ chung
$\widehat{A D C}=\widehat{A F C}=90^{\circ}$
(cạnh huyền – cạnh góc vuông)
$\Rightarrow \widehat{C}=\widehat{A}(2$ góc tương ứng ) (2)
Từ (1) và $(2) \Rightarrow \widehat{C}=\widehat{A}=\widehat{B}$
$ \Rightarrow$ Tam giác $A B C$ là tam giác đều do có 3 góc bằng nhau
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 8 chương VIII – Tam giác trang 77, 78 Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




