Giải SGK bài 5 chương 8 trang 67, 68, 69, 70 Toán 7 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Đường trung trực của một đoạn thằng. Các bài tập sau đây thuộc bài 5 chương 6 ở các trang 67, 68, 69, 70. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK trang 67, 68, 69 Toán 7 Chân trời sáng tạo tập 2
Những lời giải dưới đây sẽ giúp bạn đi tìm đáp án cho các hoạt động khởi động, khám phá, thực hành và vận dụng ở các trang 67, 68, 69 Toán 7 Chân trời sáng tạo tập 2 trong bài Đường trung trực của một đoạn thẳng một cách nhanh chóng và dễ hiểu. Cùng theo dõi ngay nhé!
Hoạt động khởi động trang 67
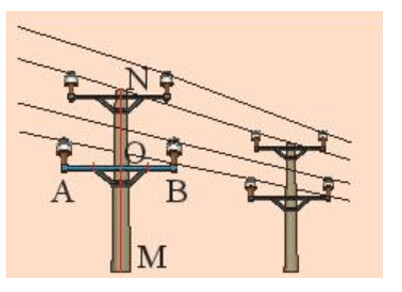
Cột điện MN vuông góc với thanh xà AB tại điểm O của đoạn thẳng AB.
Khám phá 1 trang 67
Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?
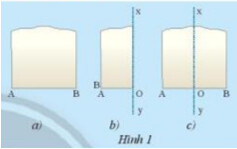
– Gấp theo hướng dẫn
Sau khi gấp $A$ trùng với $B$ thì điểm gấp trên cạnh $A B$ là $O$
$\Rightarrow \mathrm{AO}=\mathrm{BO} \Rightarrow \mathrm{O}$ là trung điểm $\mathrm{AB}$
Vi 2 mép của tờ giấy song song với nhau nên khi gấp đôi đường gấp ở giữa (xy) cũng song song với 2 cạnh của tờ giấy .
Mà 2 cạnh của tờ giấy vuông góc với $A B$ nên xy cũng vuông góc với $\mathrm{AB}$
Thực hành 1 trang 67
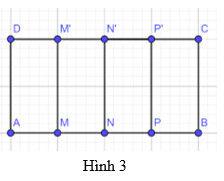
Dựa vào định nghĩa của đường trung trực
Đường trung trực của $\mathrm{AB}$ là $\mathrm{NN}^{\prime}$ vì NN’ vuông góc với $\mathrm{AB}$ tại trung điểm $\mathrm{N}$ của $\mathrm{AB}$.
Đường trung trực của AN là MM’ vì MM’ vuông góc với AN tại trung điểm $\mathrm{M}$ của AN.
Đường trung trực của $\mathrm{NB}$ là $\mathrm{PP}^{\prime}$ vì $\mathrm{PP}^{\prime}$ vuông góc với $\mathrm{NB}$ tại trung điểm $\mathrm{P}$ của $\mathrm{NB}$.
Vận dụng 1 trang 67
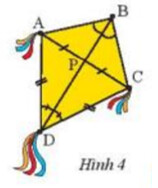
– Chứng minh P là trung điểm AC
– Chứng minh $B D$ vuông góc với $A C$
Theo giả thiết ta có $\mathrm{P}$ là trung điểm $\mathrm{AC}$ Xét tam giác APD và tam giác CPD có :
$A P=P C$ ( theo giả thiết )
DP cạnh chung
$A D=C D$ ( theo giả thiết )
Suy ra $\triangle A P D=\triangle C P D(c-c-c)$
$\Rightarrow \widehat{C P D}=\widehat{A P D}$ (2 góc tương ứng )
Mà 2 góc ở vị trí kề bù $\Rightarrow \widehat{C P D}=\widehat{A P D}=90^{\circ} \Rightarrow A C \perp B D$ và $\mathrm{P}$ là chung điểm $\mathrm{AC}$ do $\mathrm{AP}=\mathrm{PC}$
$\Rightarrow \mathrm{BD}$ là đường trung trực của $\mathrm{AC}$
Khám phá 2 trang 68
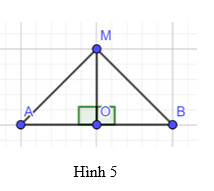
– Chứng minh 2 tam giác bằng nhau (c-g-c)
– Từ đó suy ra các cặp cạnh tương ứng bằng nhau
Theo giả thiết ta có $\mathrm{O}$ là trung điểm $\mathrm{AB} \Rightarrow \mathrm{AO}=\mathrm{OB}$ Xét tam giác $\mathrm{AOM}$ và tam giác $\mathrm{BOM}$ có :
OM là cạnh chung
\mathrm{AO}=\mathrm{OB} \\ \widehat{M O A}=\widehat{M O B}=90^{\circ}(\text { do d là trung trự } \mathrm{AB}) \\ (\mathrm{c}-\mathrm{g}-\mathrm{c}) \\ \Rightarrow M A=M B \text { ( cạnh tương ứng })
Thực hành 2 trang 69
– Sử dụng tính chất điểm thuộc trung trực của 1 đoạn thẳng cách đều 2 đầu mút
Vi M thuộc trung trực của A B \Rightarrow M A=M B \Rightarrow 7=x+2 \Rightarrow x=5
Vận dụng 2 trang 69
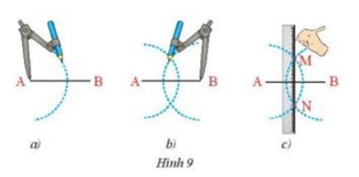
– Lấy A làm tâm vẽ cung tròn bán kính lớn hơn $\frac{1}{2} A B$ (Hình 9a)
– Lấy B làm tâm vẽ cung tròn có bán kính bẳng bán kính ở trên (Hình 9b)
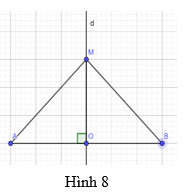
– Hai cung tròn này cắt nhau tại $\mathrm{M}$ và $\mathrm{N}$ (Hình $9 \mathrm{C}$ ). Dùng thước vẽ đường thẳng $\mathrm{MN}$. Hãy chứng minh đường thẳng $\mathrm{MN}$ chính là đường trung trực của đoạn thẳng $A B$.
Chứng minh \mathrm{M}, \mathrm{N} cùng thuộc trung trực của $ \mathrm{AB}$
Vi 2 cung tròn cắt nhau tại $\mathrm{M}$ nên $\mathrm{AM}=\mathrm{MB}=$ bán kính cung tròn
Chứng minh tương tự $\Rightarrow \mathrm{AN}=\mathrm{BN}=$ bán kính cung tròn
$\Rightarrow$ Vì $M, N$ cách đều 2 đầu mút của đoạn $A B$ nên $M, N$ thuộc trung trự của $\mathrm{AB}$
Và chỉ có 1 đường thẳng đi qua 2 điểm nên $\mathrm{MN}$ là trung trực của $\mathrm{AB}$
Giải bài tập SGK trang 70 Toán 7 Chân trời sáng tạo tập 2
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Đường trung trực của một đoạn thẳng trang 70 sách Toán 7 Chân trời sáng tạo tập 2 dưới đây nhé!
Bài 1 trang 70
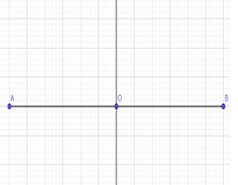
– Ta tìm giao điểm của trung trực và đoạn thẳng $A B$
– Rồi từ điểm đó tìm điểm $B$ sao cho khoảng cách từ điểm đó đên $A$ bằng $B$ và $B, A$ và giao điểm phải thẳng hàng, $\mathrm{B}$ không trùng với $\mathrm{A}$
Gọi giao điểm của $\mathrm{AB}$ và xy là $\mathrm{O}$
$\Rightarrow O$ là trung điểm $A B$ ( $D o$ xy là đường trung trực của $\mathrm{AB})$
$\Rightarrow$ Đo khoảng cách $\mathrm{AO}$ và từ điểm $O$ kẻ $O B$ sao cho $O A=$ $O B$ và nằm khác phía với điểm $A$ so với đường thẳng $x y$ ( $\mathrm{A}, \mathrm{B}, O$ thẳng hàng )
Bài 2 trang 70
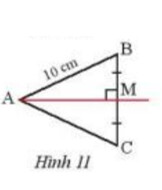
Ta chứng minh 2 tam giác AMC và AMB bằng nhau
Xét tam giác AMB và tam giác AMC có :
AM cạnh chung
$\mathrm{MB}=\mathrm{MC}$ ( do $\mathrm{M}$ là trung điểm $\mathrm{BC}$ )
$\widehat{B M A}=\widehat{C M A}=90^{\circ}$
$\Rightarrow$ Tam giác AMB $=$ tam giác AMC $(\mathrm{c}-\mathrm{g}-\mathrm{c})$
$\Rightarrow \mathrm{AB}=\mathrm{AC}=10 \mathrm{~cm}$ ( cạnh tương ứng bằng nhau)
Bài 3 trang 70
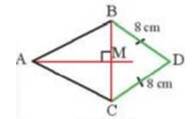
Chứng minh $D$ thuộc trung trực của $\mathrm{BC} \Rightarrow \mathrm{A}, \mathrm{M}, \mathrm{D}$ thẳng hàng
Xét tam giác $B C D$ có $B D=C D$ ( giả thiết)
$\Rightarrow D$ thuộc trung trực $\mathrm{BC}$ do cách đều 2 đầu mút đoạn $\mathrm{BC}$
Mà AM là trung trực của $\mathrm{BC}$
$\Rightarrow \mathrm{D}$ thuộc đường thẳng $\mathrm{AM}$
$\Rightarrow \mathrm{A}, \mathrm{M}, \mathrm{D}$ thẳng hàng
Bài 4 trang 70
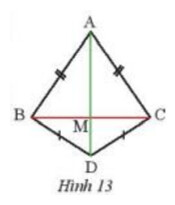
– Ta chứng minh 2 tam giác $\mathrm{ABD}$ và $\mathrm{ACD}$ bằng nhau
– Suy ra 2 tam giác BAM và CAM bằng nhau $\Rightarrow B M=$ $\mathrm{CM}$
Xét tam giác $A B D$ và tam giác $\mathrm{ACD}$ có :
$\mathrm{AB}=\mathrm{AC}$ ( giả thiết )
$\mathrm{BD}=\mathrm{CD}$ ( giả thiết)
AD cạnh chung
$\Rightarrow \triangle A B D=\triangle A C D(c-c-c) $
$ \Rightarrow \widehat{B A D}=\widehat{C A D} \text { ( } 2 \text { góc tương ứng) }$
Xét tam giác $A B M$ và ta giác $A C M$ có :
$A B=A C$ ( giả thiết )
AM cạnh chung
$\widehat{B A D}=\widehat{C A D}$ ( chứng minh trên )
$\triangle A B M=\triangle A C M(c-g-c)$
$\Rightarrow M C=M B$ ( 2 cạnh tương ứng )
$\Rightarrow \mathrm{M}$ là trung điểm $\mathrm{BC}$
Bài 5 trang 70
Chứng minh 2 tam giác bằng nhau theo trường hợp (c-c-c)
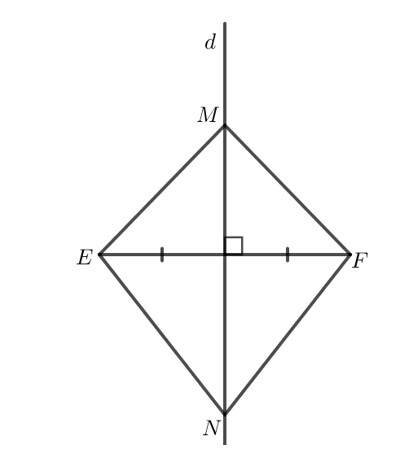
Vì $\mathrm{M}$ thuộc trung trực $\mathrm{EF}$ nên $\mathrm{ME}=\mathrm{MF}$ ( tính chất điểm thuộc trung trực)
Tương tự $\Rightarrow N E=N F$ ( tính chất điểm thuộc trung trực )
Xét 2 tam giác MEN và MFN có :
MN là cạnh chung
\mathrm{ME}=\mathrm{MF} \\ \mathrm{NE}=\mathrm{NF} \\ \Rightarrow \Delta M E N=\Delta M F N(c-c-c)
Bài 6 trang 70
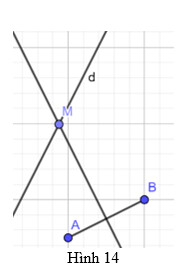
– Để $M A=M B \Rightarrow M$ thuộc trung trực $A B$
– Tìm M thuộc d
Để $M$ cách đều $A, B$ khi và chỉ khi $M$ thuộc trung trực của doạn $\mathrm{AB}$
Vi $\mathrm{M}$ phải thuộc $\mathrm{d} \Rightarrow \mathrm{M}$ là giao điểm của trung trực $\mathrm{AB}$ và đường thẳng $\mathrm{d}$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 5 chương 8 trang 67, 68, 69, 70 Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




