Giải SGK bài 6 chương 8 trang 71, 72 Toán 7 Chân trời sáng tạo tập 2
Tính chất ba đường trung trực của tam giác là bài học thuộc bài 6 chương 8 trang 71, 72 Toán 7 Chân trời sáng tạo tập 2. Dưới đây là những lời giải cực chi tiết của HocThatGioi cho những hoạt động khám phá, thực hành, vận dụng cũng như bài tập sách giáo khoa mà các bạn sẽ được học trong bài này. Cùng theo dõi ngay nhé!
Trả lời câu hỏi SGK trang 71, 72 Toán 7 chân trời sáng tạo
Cùng HocThatGioi đi tìm đáp án cho các hoạt động khởi động, thực hành và vận dụng ở các trang 71, 72 SGK Toán 7 chân trời sáng tạo trong bài Tính chất ba đường trung trực của tam giác ở ngay bên dưới nhé!
Khởi động trang 71
Điểm cách đều ba đỉnh của một tam giác là giao điểm ba đường trung trực của tam giác đó.
Khám phá 1 trang 71
– Tìm trung điểm của BC
– Vẽ đường trung trực xy đi qua trung điểm BC vuông góc cới BC
Cách 1:
Gọi trung điểm $\mathrm{BC}$ là $\mathrm{M}$
Ta kẻ xy qua M vuông góc với $\mathrm{BC}$
Cách 2:
Từ $\mathrm{B}, \mathrm{C}$ vẽ 2 cung tròn có bán kính $R \geq \frac{1}{2} B C$
2 cung tròn giao nhau tại 2 điểm $\mathrm{M}, \mathrm{N}$
Kẻ đường thẳng xy đi qua 2 điểm $\mathrm{M}, \mathrm{N}$. Ta được đường trung trực $\mathrm{xy}$ đi qua chúng
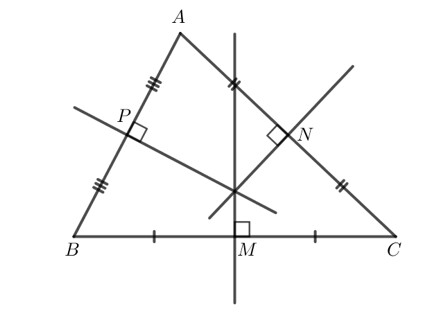
Thực hành 1 trang 71
– Cách 1 ta có thể dùng compa để vẽ 3 đường trung trực
– Cách 2 ta tìm trung điểm mỗi cạnh rồi vẽ đường trung trực của mỗi cạnh
Qua M vẽ đường thẳng vuông góc với BC.
Qua N vẽ đường thẳng vuông góc với CA.
Qua P vẽ đường thẳng vuông góc với AB.
Khi đó ta thu được ba đường trung trực của tam giác ABC.
Ta có hình vẽ sau:
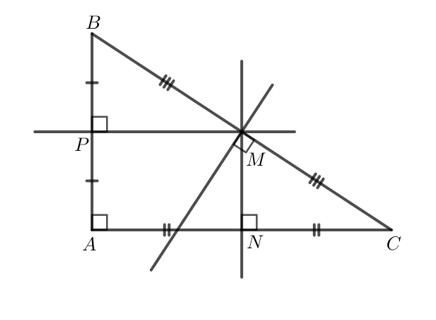
Vận dụng 1 trang 71
– Cách 1 dùng compa để vẽ các đường trung trực
– Cách 2 tìm trung điểm các cạnh rồi vẽ trung trực
Xác định ba điểm M, N, P lần lượt là trung điểm các cạnh BC, CA, AB.
Qua M vẽ đường thẳng vuông góc với BC.
Qua N vẽ đường thẳng vuông góc với CA.
Qua P vẽ đường thẳng vuông góc với AB.
Khi đó ta thu được ba đường trung trực của tam giác ABC.
Ta có hình vẽ sau:
Khám phá 2 trang 71
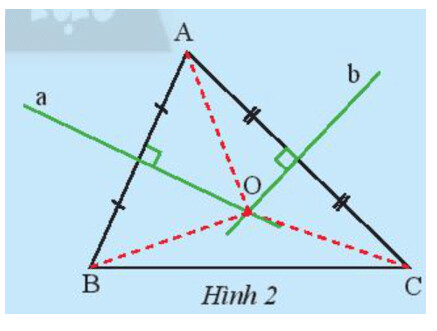
– Hãy so sánh độ dài của ba đoạn thẳng OA, OB, OC.
– Theo em, đường trung trực ứng với cạnh BC có đi qua điểm O không?
Do O nằm trên đường trung trực của AB nên OA = OB.
Do O nằm trên đường trung trực của AC nên OB = OC.
Do đó OA = OB = OC.
Do OB = OC nên O nằm trên đường trung trực của BC.
Do đó đường trung trực ứng với cạnh BC đi qua điểm O.
Thực hành 2 trang 72
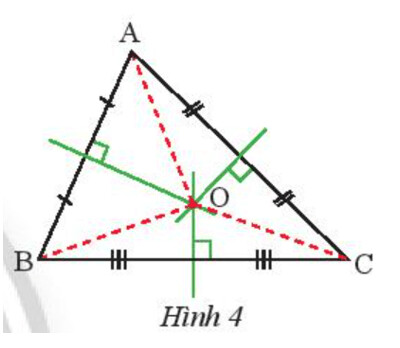
Bước 1. Vẽ tam giác ABC.
Bước 2. Lần lượt chọn trung điểm của các cạnh AB, BC, CA.
Bước 3. Qua trung điểm của cạnh AB, kẻ đường thẳng vuông góc với AB.
Qua trung điểm của cạnh BC, kẻ đường thẳng vuông góc với BC.
Qua trung điểm của cạnh CA, kẻ đường thẳng vuông góc với CA.
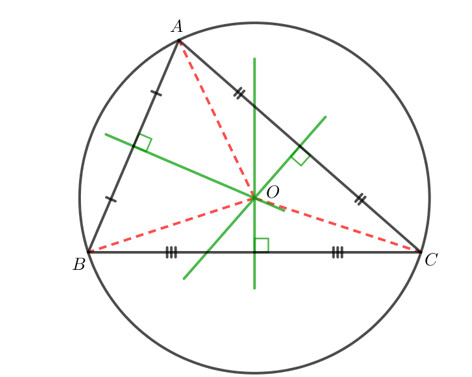
Ta thấy đường tròn tâm O bán kính OA đi qua hai điểm B và C.
Khi đó ta có hình vẽ sau:
Vận dụng 2 trang 72
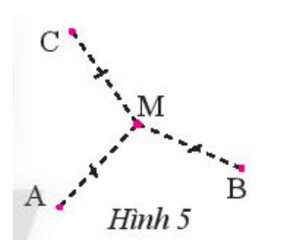
Ba điểm dân cư A, B, C tạo thành ba đỉnh của tam giác ABC.
Do M cách đều ba điểm dân cư nên MA = MB = MC.
Do MA = MB nên M nằm trên đường trung trực của AB.
Do MB = MC nên M nằm trên đường trung trực của BC.
Do đó M là giao điểm ba đường trung trực của tam giác ABC.
Vậy M là giao điểm ba đường trung trực của tam giác ABC với các đỉnh là các điểm dân cư A, B, C.
Giải bài tập SGK trang 72 Toán 7 chân trời sáng tạo
Những bài tập SGK ở cuối bài Tính chất ba đường trung trực của tam giác trang 72 sách Toán 7 chân trời sáng tạo sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 1 trang 72
a) Xác định điểm O cách đều ba đỉnh của mỗi tam giác
b) Nêu nhận xét của em về vị trí của điểm O trong mỗi trường hợp.
– Vẽ 3 tam giác và xác định điểm O
a) Gọi ba đỉnh của tam giác là A; B; C.
Điểm O cách đều ba đỉnh của tam giác ABC nên O là giao điểm ba đường trung trực của tam giác ABC.
Tam giác nhọn
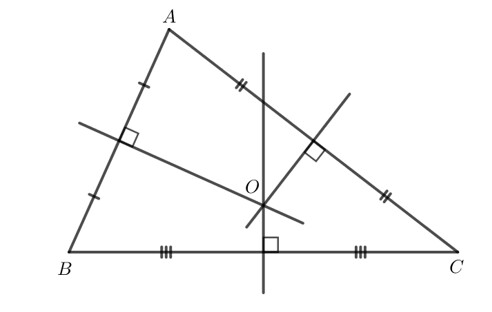
Tam giác vuông
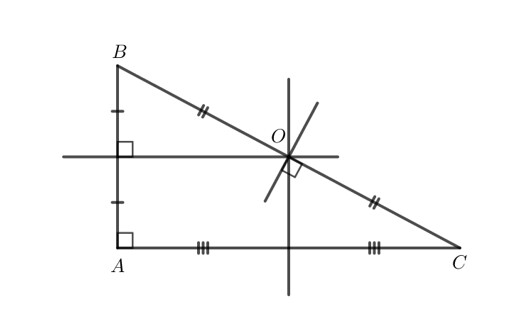
Tam giác tù
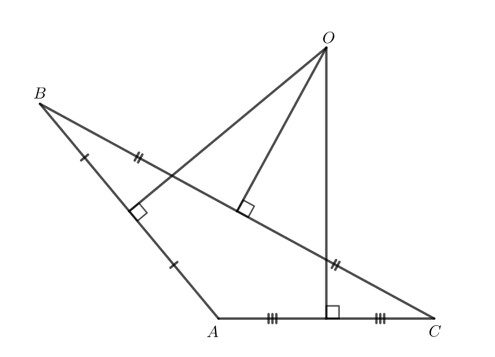
b)
– Với tam giác nhọn, giao điểm ba đường trung trực của tam giác nằm trong tam giác đó.
– Với tam giác vuông, giao điểm ba đường trung trực của tam giác là trung điểm cạnh huyền của tam giác đó.
– Với tam giác tù, giao điểm ba đường trung trực của tam giác nằm ngoài tam giác đó.
Bài 2 trang 72
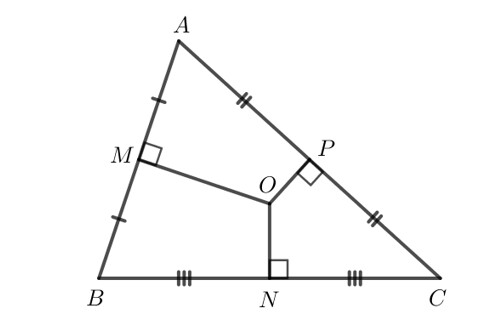
O là điểm cách đều 3 đỉnh của tam giác $\mathrm{ABC}$ nên $\mathrm{O}$ là giao điểm ba đường trung trực của tam giác $\mathrm{ABC}$.
Khi đó do $M, N, P$ lần lượt là trung điểm các cạnh $A B, B C, C A$ nên $M O \perp A B$, $\mathrm{NO} \perp \mathrm{BC}, \mathrm{PO} \perp \mathrm{AC}$.
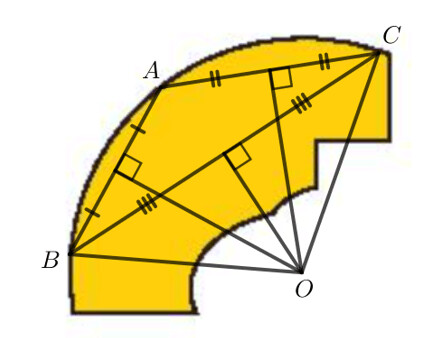
Bài 3 trang 72
Để xác định bán kính của chiếc đĩa cổ, ta làm như sau:
– Bước 1. Xác định ba điểm A, B, C thuộc đường viền của chiếc đĩa.
– Bước 2. Xác định giao điểm O của ba đường trung trực của tam giác ABC.
– Bước 3. Khi đó độ dài đoạn OB là bán kính của chiếc đĩa cổ.
Ta có hình vẽ sau:
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 6 chương 8-Tính chất ba đường trung trực của tam giác trang 71, 72 Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




