Giải SGK bài Tam giác bằng nhau chương 8 Toán 7 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Tam giác bằng nhau. Các bài tập sau đây thuộc bài 2 chương 8 – Tam giác trang 48, 49, 50. 51, 52, 53, 54, 55, 56, 57, 58 Toán 7 Chân trời sáng tạo tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Tam giác bằng nhau
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 48, 49, 50, 51, 52, 53, 54, 55, 56, 57 trong bài Tam giác bằng nhau. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 48
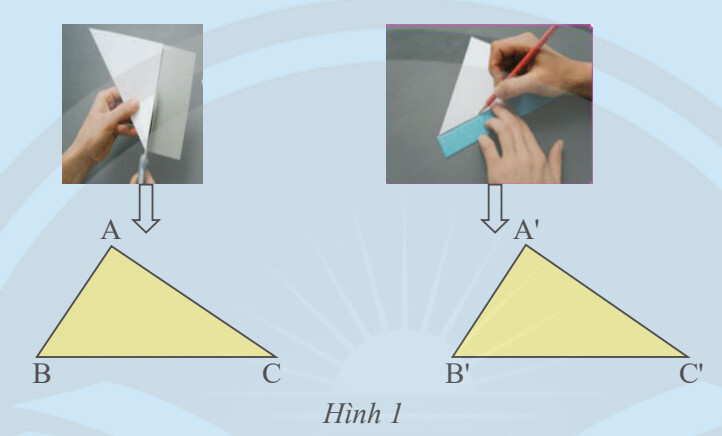
Ta cắt 2 tam giác như hướng dẫn.
Ta thấy 2 tam giác có các cặp góc bằng nhau:
$\widehat{A}=\widehat{A^{\prime}} ; \widehat{B}=\widehat{B^{\prime}} ; \widehat{C}=\widehat{C^{\prime}}$
2 tam giác có các cặp cạnh bằng nhau:
$A C=A^{\prime} C^{\prime} ; A B=A^{\prime} B^{\prime} ; B C=B^{\prime} C^{\prime}$
Thực hành 1 trang 49
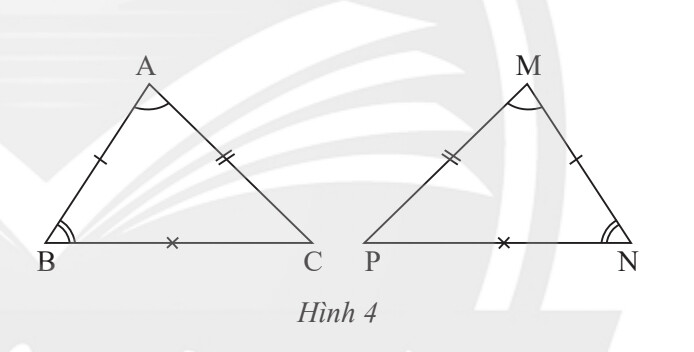
Ta dựa vào định nghĩa về 2 tam giác bằng nhau.
$\Rightarrow \triangle A B C=\triangle M N P$ do có các cặp góc và cạnh tương ứng bằng nhau.
Các cặp góc bằng nhau là: $\widehat{A}=\widehat{M} ; \widehat{B}=\widehat{N} ; \widehat{C}=\widehat{P}$
Các cặp cạnh bằng nhau là: $A B=M N ; A C=M P ; B C=P N$
Vận dụng 1 trang 49
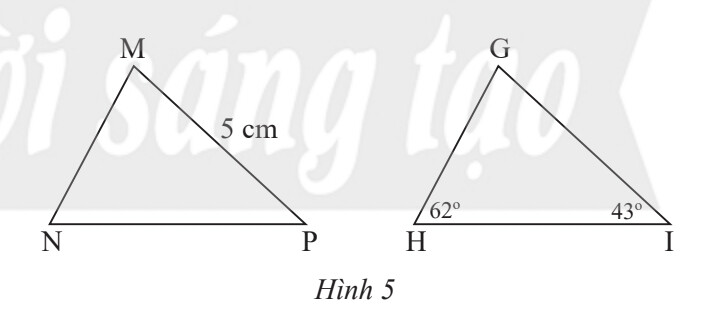
Áp dụng các tính chất của 2 tam giác bằng nhau.
Theo định lí tổng 3 góc trong tam giác ta có :
$ \widehat{G}+\widehat{H}+\hat{I}=180^{\circ} \Rightarrow \widehat{G}=180^{\circ}-62^{\circ}-43^{\circ}=75^{\circ} $
Vì $ \Delta M N P=\Delta G H I \Rightarrow \widehat{G}=\widehat{M}$ (2 góc tương ứng)
$ \Rightarrow \widehat{M}=75^{\circ} $
$ \Delta M N P=\Delta G H I \Rightarrow M P=G I $ (2 cạnh tương ứng)
$ \Rightarrow G I=5 \mathrm{~cm} $.
Hoạt động 2 trang 50
-Vẽ đoạn thẳng B’C’= BC
-Vẽ cung tròn tâm B’có bán kính bằng BA, vẽ cung trong tâm C’ có bán kính bằng CA.
-Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung)
-Vẽ các đoạn thẳng B’A, C’A’, ta được tam giác A’B’C’ (Hình 6b)
Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
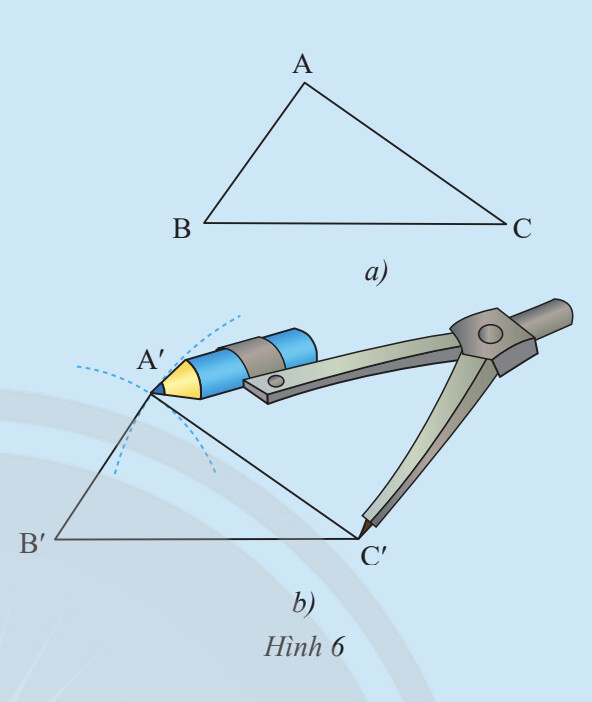
Vẽ hình và so sánh độ dài các cạnh các góc của 2 tam giác.
Xét tam giác ABC và tam giác A’B’C’ có:
BC = B’C’ ( giả thiết )
B’A’ = BA
A’C’ = CA
Hai tam giác có thể đặt chồng khít lên nhau nên 2 tam giác bằng nhau.
Hoạt động 3 trang 51
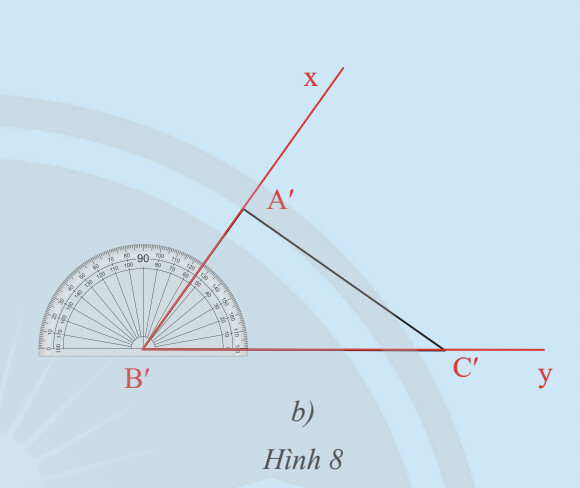
– Vẽ $\widehat{x B^{\prime} y}=\widehat{A B C}$
– Trên tia $B^{\prime} x$ lấy đoạn $B^{\prime} A^{\prime}=B A$.
– Trên tia B’y lấy đoạn $B^{\prime} C^{\prime}=B C$.
-Vẽ đoạn $A^{\prime} C^{\prime}$, ta được tam giác $A^{\prime} B^{\prime} C^{\prime}($ Hình 8b)
Em hãy cắt rời tam giác $A^{\prime} B^{\prime} C^{\prime} r a$ khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác $A^{\prime} B^{\prime} C^{\prime}$ ên tam giác $A B C$ hay không.
Theo em, hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ trong trường hợp này có bằng nhau hay không?
– Vẽ góc trước rồi vẽ 2 cạnh theo đề bài
– Cắt giấy theo hình vẽ được
– So sánh hai tam giác xem chúng bằng nhau hay không
Ta thấy 2 tam giác có thể chồng khít lên nhau nên 2 tam giác bằng nhau.
Chú ý: 2 tam giác bằng nhau khi có 2 cặp cạnh bằng nhau và góc xen giữa 2 cặp cạnh đó cũng bằng nhau .
Hoạt động 4 trang 52
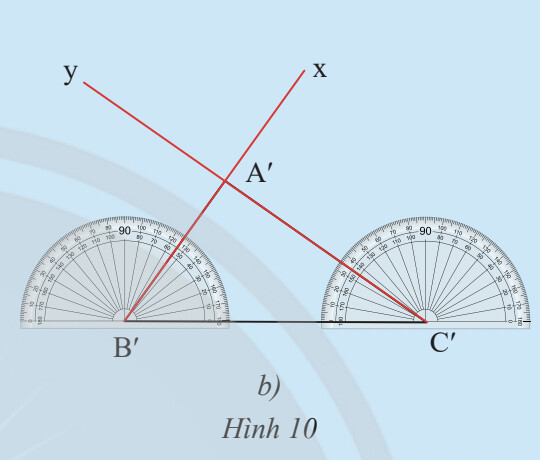
-Vẽ đoạn thẳng $B^{\prime} C^{\prime}=B C$.
-ở về cùng một phía của tờ giấy đối với đường thẳng $B^{\prime} C^{\prime}$ vẽ $\widehat{C^{\prime} B^{\prime} x}=\widehat{C B A}$, và vẽ $\widehat{B^{\prime} C^{\prime} y}=\widehat{B C A}$
-Vẽ giao điểm A’của hai tia B’x và C’y, ta được tam giác A’B’C’ (Hình 10b).
Em hãy cắt rời tam giác $A^{\prime} B^{\prime} C^{\prime} r a$ khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’ên tam giác ABC hay không.
Theo em, hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ trong trường hợp này có bằng nhau hay không?
– Ta vẽ đoạn thẳng trước rồi từ 2 đầu đoạn thẳng lần lượt vẽ các góc theo số đo của tam giác ABC
– Sau khi cắt và chồng lên nhau sẽ thu được kết quả
Ta thấy 2 tam giác có thể chồng khít lên nhau nên 2 tam giác bằng nhau.
Từ đó ta suy ra 2 tam giác bằng nhau khi có 2 góc bằng nhau và cạnh xen giữa 2 góc đó cũng bằng nhau
Thực hành 2 trang 54
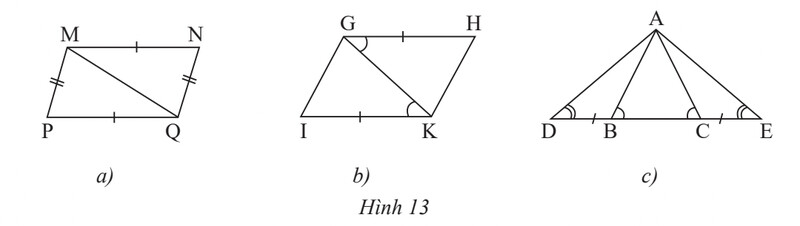
Dựa vào các trường hợp 2 tam giác bằng nhau c-c-c; c-g-c; g-c-g.
a) Ta thấy tam giác MNQ = tam giác MPQ ( c-c-c )
b) Ta thấy tam giác GHK = tam giác GIK ( c-g-c )
c) Ta thấy tam giác ADB = tam giác ACE ( g-c-g )
Tam giác ADC = tam giác AEB ( g-c-g )
Thực hành 3 trang 54
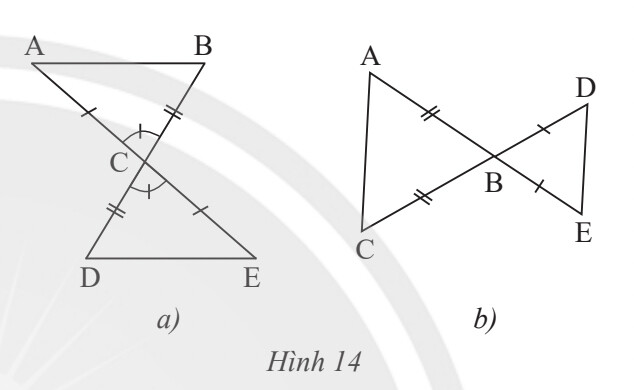
Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g.
a) Xét $\triangle A B C$ và $\Delta E D C$, ta có:
$A C=C E$
$\widehat{A C B}=\widehat{D C E}$ ( 2 góc đối đỉnh )
$C B=C D$
$\Rightarrow \Delta A B C=\Delta E D C $ (c.g.c)
b) Ta thấy 2 tam giác $A B C$ và $B D E$ không bằng nhau vì:
$A C \neq B E ; B C \neq B D ; D E \neq A C$
Vận dụng 2 trang 54
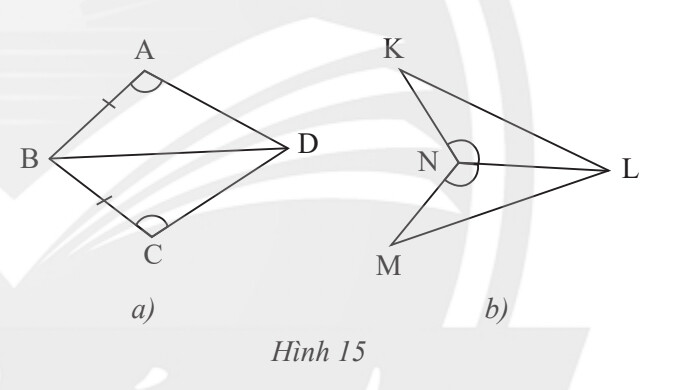
Dựa vào trường hợp cạnh – góc – cạnh.
a) Theo trường hợp cạnh – góc – cạnh ta cần AD = CD để 2 tam giác bằng nhau
b) Theo trường hợp cạnh – góc – cạnh ta cần KN = MN để 2 tam giác bằng nhau
Vận dụng 3 trang 54
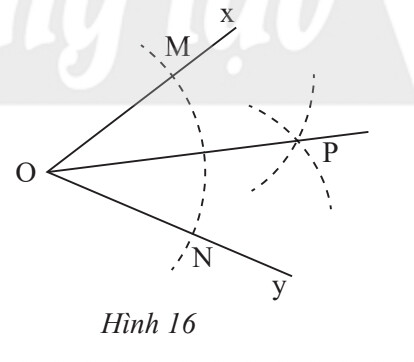
Ta chứng minh 2 tam giác bằng nhau bằng phương pháp cạnh – cạnh – cạnh.
Vì $M, N$ thuộc đường tròn tâm $O$ có cùng bán kính nên $O M=O N$ = bán kính cung tròn tâm 0
Từ $\mathrm{M}, \mathrm{N}$ vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại $\mathrm{P}$
Suy ra $P$ thuộc cả 2 cung tròn tâm $M, N$ có cùng bán kính nên $M P=N P$
Xét tam giác OMP và tam giác ONP ta có :
$\mathrm{OM}=\mathrm{ON}$
$OP$ cạnh chung
$\mathrm{MP}=\mathrm{NP}$
$\Rightarrow \triangle O M P=\triangle O N P(\mathrm{c}-\mathrm{c}-\mathrm{c})$
$\Rightarrow \widehat{M O P}=\widehat{P O N}$ (2 góc tương ứng)
Do đó, OP là phân giác $\widehat{x O y}$
Hoạt động 5 trang 55
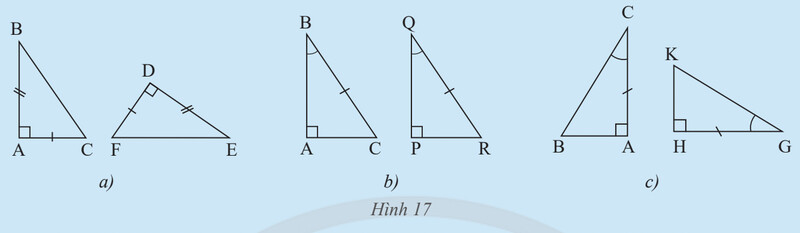
Dựa vào tam giác vuông có sẵn 1 cặp góc bằng nhau ( góc vuông ) nên chỉ cần tìm điều kiện để các cặp cạnh, cặp góc còn lại bằng nhau.
a) Xét $\triangle A B C$ và $\triangle D E F$ có:
$A B=D E(g t)$
$\widehat{B A C}=\widehat{E D F}(\mathrm{gt})$
$\mathrm{AC}=\mathrm{DF}(\mathrm{gt})$
$\Rightarrow \triangle A B C=\triangle D E F$ (c-g-c)
b) Ta có: $\widehat{B}+\widehat{C}=\widehat{Q}+\widehat{R}=90^0$
Mà $\widehat{B}=\widehat{Q} \Rightarrow \widehat{C}=\widehat{R}$
Xét $\triangle A B C$ và $\triangle P Q R$ có:
$\widehat{C}=\widehat{R}(\mathrm{gt})$
$\mathrm{BC}=\mathrm{QR}(\mathrm{gt})$
$\widehat{B}=\widehat{Q}(\mathrm{gt})$
$\Rightarrow \triangle A B C=\triangle P Q R$ ( g-c-g $)$
c) Xét $\triangle A B C$ và $\triangle H K G$ có:
$\widehat{C}=\widehat{G}(\mathrm{gt})$
$\mathrm{AC}=\mathrm{HG}(\mathrm{gt})$
$\widehat{A}=\widehat{H}(\mathrm{~g})$
$\Rightarrow \Delta A B C=\Delta H K G(\mathrm{~g}-\mathrm{c}-\mathrm{g})$
Thực hành 4 trang 56
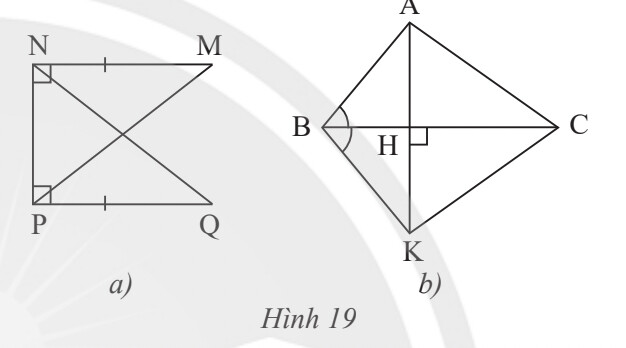
Sử dụng các trường hợp bằng nhau của tam giác vuông.
a) Xét $\triangle M N P$ và $ \triangle Q P N$, ta có:
$N M=P Q$
NP chung
$ \widehat{M N P}=\widehat{N P Q}$
$ \Rightarrow \Delta M N P=\Delta Q P N \text { (c.g.c) }$
b) Ta thấy $\triangle A B H=\Delta K B H$ (g-c-g) và $\Delta A H C=\Delta K H C$ (c-g-c)
$\Delta A B C=\Delta K B C$
Thực hành 6 trang 56
– Vẽ góc vuông xA’ý, trên cạnh A’y vẽ đoạn A’C’= AC.
– Vẽ cung tròn tâm C’ bán kính bằng BC cắt A’x tại B’
Cắt rời tam giác A’B’C’. Em hãy cho biết có thể đặt chồng khít tam giác này lên tam giác kia không.
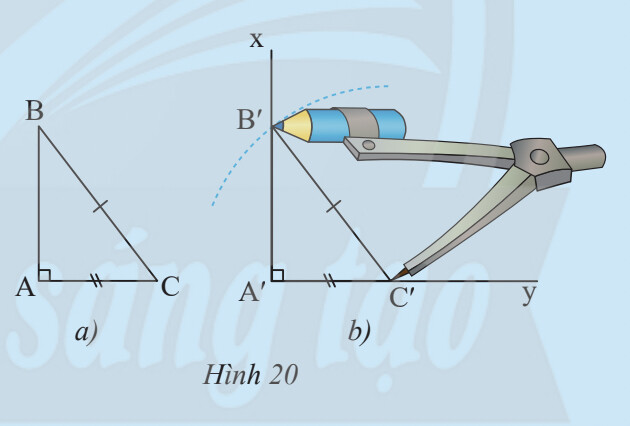
– Ta vẽ 2 cạnh trước rồi sau đó vẽ góc
– Cắt và so sánh 2 hình
Ta nhận thấy 2 hình bằng nhau
Chồng lên nhau vì vừa khít
Thực hành 5 trang 57
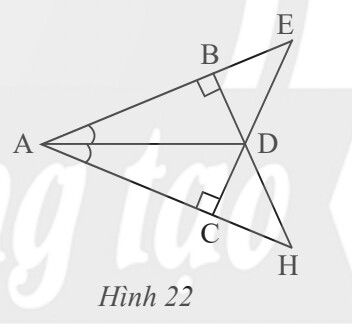
– Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g
– Sử dụng các trường hợp bằng nhau của tam giác vuông: 2 cạnh góc vuông; cạnh góc vuông – góc nhọn kề; cạnh huyền – góc nhọn.
+) Xét tam giác $A B D$ vuông tại $B$ và tam giác $A C D$ vuông tại $C$ :
$\widehat{B A D}=\widehat{C A D}$ (theo giả thiết).
$A D$ chung.
Do đó $\triangle \mathrm{ABD}=\triangle \mathrm{ACD}$ (cạnh huyền – góc nhọn).
Suy ra DB = DC ( 2 cạnh tương ứng).
+) Xét tam giác DBE vuông tại B và tam giác $D C H$ vuông tại C:
$\mathrm{DB}=\mathrm{DC}$ (chứng minh trên).
$\widehat{B \mathrm{D} E}=\widehat{C \mathrm{DH}}$ (2 góc đối đỉnh).
Do đó $\triangle \mathrm{DBE}=\triangle \mathrm{DCH}$ (góc nhọn – cạnh góc vuông).
Suy ra DE $=$ DH (2 cạnh tương ứng).
Do $\triangle A B \mathrm{D}=\Delta A C \mathrm{D}$ (cạnh huyền – góc nhọn) nên $\widehat{A \mathrm{D} B}=\widehat{A \mathrm{D} C}$ (2 góc tương ứng).
Mà $\widehat{B \mathrm{D} E}=\widehat{C \mathrm{D} H}$ nên $\quad \widehat{A \mathrm{D} B}+\widehat{B \mathrm{D} E}=\widehat{A \mathrm{D} C}+\widehat{C \mathrm{D} H}$ hay $\widehat{A \mathrm{DE}}=\widehat{A \mathrm{DH}}$
+) Xét tam giác ADE và tam giác ADH:
AD chung.
$\widehat{A \mathrm{D} E}=\widehat{A \mathrm{D} H}$ (chứng minh trên).
$\mathrm{DE}=\mathrm{DH}$ (chứng minh trên).
Do đó $\triangle \mathrm{ADE}=\triangle \mathrm{ADH}$ (c.g.c).
Giải bài tập SGK bài Tam giác cân
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Tam giác cân trang 57, 58 sách Toán 7 chân trời sáng tạo tập 2 dưới đây nhé!
Bài tập 1 trang 57
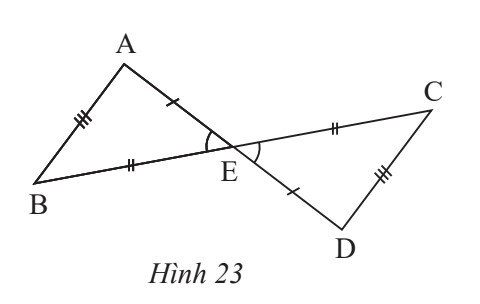
a) $\triangle \mathrm{ABE}=\triangle$ ?
b) $\triangle \mathrm{EAB}=\triangle$ ?
c) $\triangle ?=\triangle C D E$.
Sử dụng 3 trường hợp bằng nhau của tam giác.
Quan sát Hình 23 ta thấy:
a) Xét $\triangle \mathrm{ABE}$ và $\triangle \mathrm{DCE}$ có:
$A B=D C$ (theo giả thiết).
$\mathrm{BE}=\mathrm{CE}$ (theo giả thiết).
$A E=D E$ (theo giả thiết).
Suy ra $\triangle A B E=\triangle D C E$ (c.c.c).
Vậy $\triangle \mathrm{ABE}=\triangle \mathrm{DCE}$.
b) $D o \triangle A B E=\triangle D C E$ (chứng minh trên) nên $\triangle E A B=\triangle E D C$.
c) $D o \triangle \mathrm{ABE}=\triangle \mathrm{DCE}$ (chứng minh trên) nên $\triangle \mathrm{BAE}=\triangle \mathrm{CDE}$.
Bài tập 2 trang 57
2 tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Vì $\triangle D E F=\Delta H I K $
$ \Rightarrow \widehat{D}=\widehat{H} $ ( 2 góc tương ứng )
Mà $\widehat{D}=73^0$
$ \Rightarrow \widehat{H}=73^0$
Vì $ \Delta D E F=\Delta H I K $
$ \Rightarrow D E=H I ; E F=I K ; D F=H K $ ( các cạnh tương ứng )
Vậy $\widehat{H}=73^o ; H I=5 \mathrm{~cm} ; E F=7 \mathrm{~cm}$
Bài tập 3 trang 58
Các góc ở đỉnh tương ứng bằng nhau suy ra thứ tự các đỉnh của 2 tam giác bằng nhau.
Hai tam giác bằng nhau thì các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Áp dụng định lí tổng ba góc trong một tam giác ta có:
Xét tam giác $A B C$ có: $\widehat{B}=180^{\circ}-\widehat{A}-\widehat{C}$.
Xét tam giác $D E F$ có: $\widehat{F}=180^{\circ}-\widehat{E}-\widehat{D}$.
Mà $\widehat{A}=\widehat{E}$ và $\widehat{C}=\widehat{D}$ nên $\widehat{B}=\widehat{F}$.
Do đó $\triangle \mathrm{ABC}=\triangle \mathrm{EFD}$.
Khi đó $A B=E F$ (2 cạnh tương ứng), $B C=F D$ (2 cạnh tương ứng), $C A=D E$ (2 cạnh tương ứng).
Vậy $\widehat{B}=\widehat{F}, \mathrm{AB}=\mathrm{EF}, \mathrm{BC}=\mathrm{FD}, \mathrm{CA}=\mathrm{DE}$.
Bài tập 4 trang 58
– Sử dụng tích chất các góc, cạnh tương ứng của 2 tam giác bằng nhau.
Vì $\triangle \mathrm{ M N P}$=$\triangle \mathrm{ D E F} $
$ \Rightarrow D E=M N ; E F=N P ; D F=M P $(các cạnh tương ứng)
$\Rightarrow N P=6 \mathrm{~cm} $
$ \Rightarrow$ Chu vi tam giác MNP là:
$ \mathrm{c}=\mathrm{MN}+\mathrm{MP}+\mathrm{NP}=4+5+6=15(\mathrm{~cm})$
Bài tập 5 trang 58
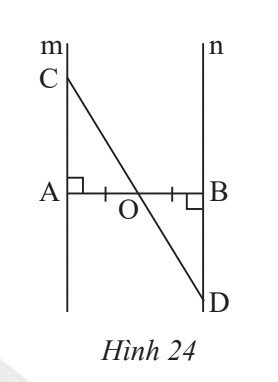
– Chứng minh tam giác OAC và tam giác OBD bằng nhau
– Từ đó suy ra OC = OD ( 2 cạnh tương ứng)
Xét $\triangle \mathrm{O A C}$ và $\triangle \mathrm{O B D}$, ta có:
$\widehat{C O A}=\widehat{B O D}$ ( 2 góc đối đỉnh)
$A O=B O$
$\widehat{A}=\widehat{B}$
$\Rightarrow \triangle O A C=\triangle O B D(\mathrm{~g}-\mathrm{c}-\mathrm{g})$
$\Rightarrow C O=D O$ ( cạnh tương ứng )
$\Rightarrow \mathrm{O}$ là trung điểm $\mathrm{CD}$
Bài tập 6 trang 58
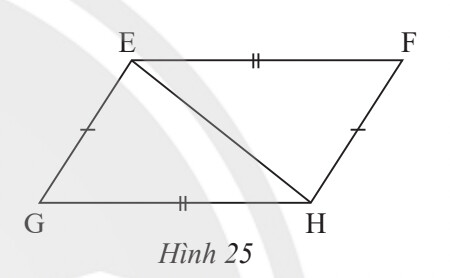
a) $\triangle \mathrm{EFH} = $\triangle \mathrm{HGE}$.
b) EF // HG.
– Chứng minh 2 tam giác bằng nhau (c-c-c)
– Chứng minh 2 góc ở vị trí so le trong bằng nhau
a) Xét $\triangle \mathrm{ E F H}$ và $\Delta H G E$ có :
$\mathrm{EF}=\mathrm{HG} ; \mathrm{FH}=\mathrm{GE} ; \mathrm{EH}$ chung
$\Rightarrow \Delta E F H=\Delta H G E(\mathrm{c}-\mathrm{c}-\mathrm{c})$
$\Rightarrow \widehat{F E H}=\widehat{E H G}$ ( 2 góc tương ứng )
b) Vî $\widehat{F E H}=\widehat{E H G}$
Mà 2 góc này ở vị trí so le trong
Do đó, EF // HG (Dấu hiệu nhận biết)
Bài tập 7 trang 58
2 tam giác bằng nhau theo trường hợp c-g-c
Xét $\Delta F I G$ và $\Delta F I H$ có $:$
Fl chung
$\widehat{G F I}=\widehat{H F I}$ ( do FI là phân giác $\widehat{G F H}$ )
$\mathrm{FG}=\mathrm{FH}$ (giả thiết )
$\Rightarrow \Delta F I G=\Delta F I H(\mathrm{c}-\mathrm{g}-\mathrm{c})$
Bài tập 8 trang 58
a) $AD = BC$
b) $\triangle \mathrm{EAB}=\triangle \mathrm{ECD}$
c) OE là tia phân giác của góc xOy.
Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g để chứng minh các tam giác bằng nhau rồi suy ra các cạnh tương ứng bằng nhau hoặc các góc tương ứng bằng nhau.
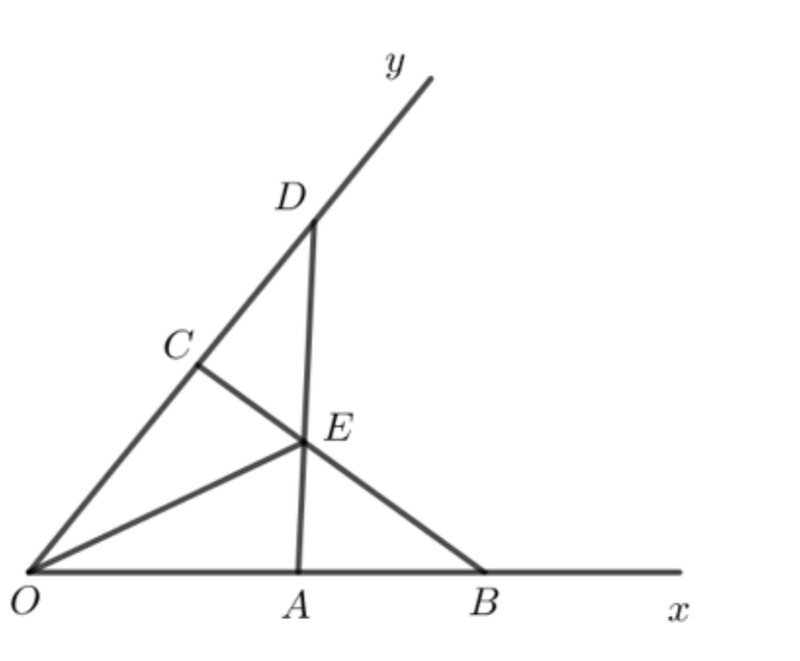
a) Xét hai tam giác OAD và OCB có:
$O A=O C$ (theo giả thiết).
$\widehat{O}$ chung.
$O D=O B$ (theo giả thiết).
Do đó $\triangle \mathrm{ O A D}=\triangle \mathrm{O C B}$ (c.g.c).
Suy ra $A D=B C$ ( 2 cạnh tương ứng).
b) $D o O A=O C, O B=O D$ nên $O B-O A=O D-O C$ hay $A B=C D$.
Do $\triangle \mathrm{OAD}=\triangle \mathrm{OCB}$ (c.g.c)
nên $\widehat{O D A}=\widehat{O B C}$ (2 góc tương ứng).
$\widehat{E C D}$ là góc ngoài tại đỉnh $C$ của tam giác $O B C$
nên $\widehat{E C D}=\widehat{C O B}+\widehat{O B C}(1)$
$\widehat{E A B}$ là góc ngoài tại đỉnh $A$ của tam giác $O A D$
nên $\widehat{E A B}=\widehat{A O D}+\widehat{O D A}(2)$
Từ (1) và (2) suy ra $\widehat{E C D}=\widehat{E \mathrm{AB}}$.
Xét hai tam giác EAB và ECD có:
$\widehat{E \mathrm{AB}}=\widehat{E C \mathrm{D}}$ (chứng minh trên).
$A B=C D$ (chứng minh trên).
$\widehat{E B A}=\widehat{E \mathrm{DC}}$ (chứng minh trên).
Do đó $\triangle \mathrm{EAB}=\triangle \mathrm{ECD}$ (g.c.g).
c) $D o \triangle E A B=\triangle E C D$ (g.c.g)
nên $B E=D E$ (2 cạnh tương ứng).
Xét hai tam giác $\mathrm{ODE}$ và $\mathrm{OBE}$ có:
$\mathrm{OD}=\mathrm{OB}$ (theo giả thiết).
OE chung.
$D E=B E$ (theo giả thiết).
Do đó $\triangle \mathrm{ODE}=\triangle \mathrm{OBE}$ (c.c.c).
Suy ra $\widehat{E O D}=\widehat{E O B}$ (2 góc tương ứng).
Vậy OE là tia phân giác của $\widehat{x O y}$.
Bài tập 9 trang 58
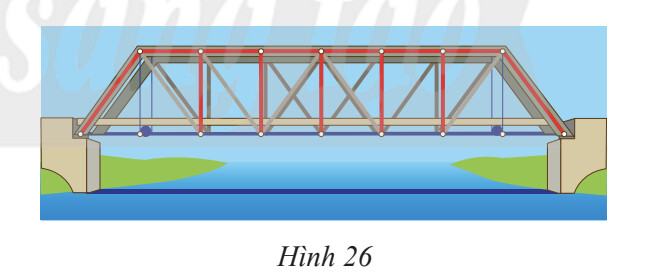
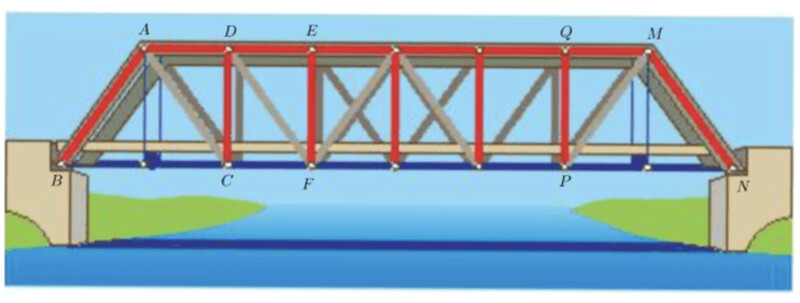
Đặt tên các điểm như hình trên.
Dựa vào hình trên ta có các cặp tam giác bằng nhau như sau:
$\triangle \mathrm{ABC} = \triangle \mathrm{ MNP}; \triangle \mathrm{ ADC} =\triangle \mathrm{ MQP}; \triangle \mathrm{ ADC} =\triangle \mathrm{ DEF}$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 2 chương 8 – Tam giác trang 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58 Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




