Giải SGK bài 4 chương 8 trang 64, 65, 66 Toán 7 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Đường vuông góc và đường xiên. Đây là bài học thuộc bài 4 chương 8 trang 64, 65, 66 sách Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi trong SGK bài Đường vuông góc và đường xiên
Dưới đây là phương pháp và bài giải chi tiết cho câu hỏi mở đầu, hoạt động khám phá, vận dụng cùng phần thực hành ở các trang 64, 65, 66 trong bài Đường vuông góc và đường xiên. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi khởi động trang 64
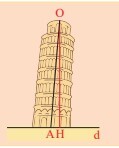
Dựa vào hình trên, thực hiện kiểm tra ta thấy dây dọi $OH$ vuông góc với đường thẳng $d$.
Hoạt động khám phá 1 trang 64
– Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh $a,b,c$
– Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc $A,B,C$ là các góc đối diện với ba cạnh $a,b,c$.
– Nêu nhận xét của em về hai kết quả sắp xếp trên.
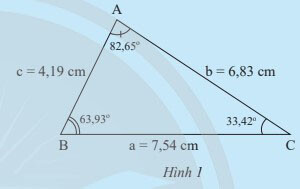
Ta dựa vào số đo các cạnh, góc của tam giác để sắp xếp theo độ lớn
– Độ dài các cạnh từ nhỏ đến lớn là $c, b, a$
– Các góc từ nhỏ đến lớn là $C, B, A$
– Ta thấy trong tam giác $ABC$ cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.
Thực hành 1 trang 64
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác $ABC$ trong Hình 3b.
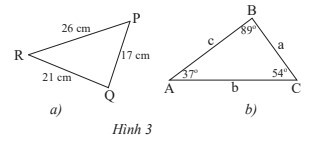
Sử dụng định lí về góc đối diện cạnh trong tam giác
a) Ta có độ dài các cạnh tam giác $PQR$ theo thứ tự từ nhỏ đến lớn là $PQ, QR, RP$
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ra có các góc tam giác $PQR$ theo thứ tự từ nhỏ đến lớn là $R, P, Q$
b) Ta có số đo các góc theo tứ tự từ nhỏ đến lớn của tam giác $ABC$ là $A, C, B$
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ta có các cạnh tam giác $ABC$ theo thứ tự từ nhỏ đến lớn là $a, c, b$.
Vân dụng 1 trang 64
b) Cho tam giác $\mathrm{ABC}$ vuông tại $\mathrm{A}$. Cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác $A B C$ ?
Sử dụng tính chất góc đối diện và cạnh trong tam giác.
a) Vì tổng số đo 3 góc trong tam giác là $180^{\circ}$ mà $\mathrm{F}$ là góc tù
$\Rightarrow \mathrm{F}>90^{\circ}$ do $\mathrm{F}$ là góc tù
$\Rightarrow \mathrm{D}+\mathrm{E}<180^{\circ}-90^{\circ}$
$\Rightarrow$ $F$ là góc lớn nhất trong tam giác $D E F$
$\Rightarrow$ Cạnh đối diện góc $\mathrm{F}$ sẽ là cạnh lớn nhất tam giác $DEF$
$\Rightarrow \mathrm{DE}$ là cạnh lớn nhất
b) Tam giác $A B C$ có góc $A$ là góc vuông nên ta có
$\Rightarrow \widehat{B}+\widehat{C}=90^{\circ} \Rightarrow \widehat{B} ; \widehat{C}<90^{\circ}$
$\Rightarrow$ $A$ là góc lớn nhất tam giác $\mathrm{ABC}$
$\Rightarrow \mathrm{BC}$ là cạnh lớn nhất tam giác $\mathrm{ABC}$ do đối diện góc $\mathrm{A}$
Hoạt động khám phá 2 trang 65
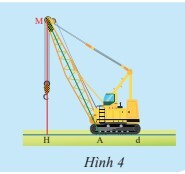
Ta có thể đo số đo các góc và tìm ra góc vuông (góc có số đo là $90^{\circ}$ )
Ta thấy $\widehat{M H A}=90^{\circ}$ nên $\mathrm{MH}$ vuông góc với $d$
Vì $\widehat{M A H}<90^{\circ}$ nên $MA$ không vuông góc với $d$
Hoạt động khám phá 3 trang 65
a) Hãy cho biết trong hai góc $AHB$ và $ABH$, góc nào lớn hơn
b) Từ câu a, hãy giải thích vì sao $AB \gt AH$.
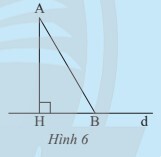
– Ta sử dụng định lí về tổng số đo 3 góc trong 1 tam giác.
– Ta sử dụng định lí: Trong tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn.
a) Xét tam giác AHB vuông tại $\mathrm{H}$ ( theo giả thiết )
$\Rightarrow \widehat{A B H}+\widehat{H A B}=90^{\circ} \\\\ \Rightarrow \widehat{A H B}>\widehat{A B H}$ (Do $\widehat{A H B}=90^{\circ}$ và $\widehat{A B H}\widehat{A B H}$ ( chứng minh a )
Mà $\widehat{A H B}$ đối diện với cạnh $\mathrm{AB}, \widehat{A B H}$ đối diện với cạnh $\mathrm{AH}$.
$$\Rightarrow A B>A H$$
Thực hành 2 trang 65
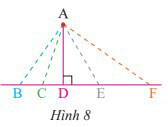
Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.
Theo hình 8 ta thấy $AD$ là đường ngắn nhất vì $AD$ vuông góc với $BF$
Các đường xiên là $AB, AC, AE, AF$.
Vân dụng 2 trang 66
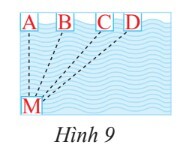
Sử dụng tính chất trong các đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên.
Ta gọi thành hồ bơi đối diện là đường thẳng $AD$
Bạn Minh bơi đường ngắn nhất khi bơi từ điểm $M$ 1 đường vuông góc với $AD$ do đoạn thẳng nối từ 1 điểm ở ngoài một đường thẳng đến các điểm trên đường thẳng đó, đường vuông góc luôn ngắn hơn tất cả các đường xiên .
Ta thấy $AM$ vuông góc $AD$ nên $AM$ là đường ngắn nhất
Giải bài tập SGK bài Đường vuông góc và đường xiên
Phần tiếp theo sẽ cung cấp cho các bạn phương pháp cùng lời giải trong phần bài tập trang 66 cực kỳ dễ hiểu và chi tiết. Cùng HocThatGioi rèn luyện và nâng cao kỹ năng giải quyết các vấn đề thực tế thông qua các phương pháp, công thức toán học từ bài Đường vuông góc và đường xiên ở trên.
Bài 1 trang 66
b) So sánh các cạnh của tam giác $\mathrm{ABC}$ có $\widehat{\mathrm{A}}=50^{\circ}, \widehat{\mathrm{C}}=50^{\circ}$.
– Sử dụng định lí về góc đối diện cạnh trong tam giác
– Sử dụng tính chất tam giác cân và tính góc còn lại của tam giác để so sánh độ dài các cạnh
a) Theo đề bài ta có $\mathrm{AB}=4 \mathrm{~cm}, \mathrm{BC}=7 \mathrm{~cm}, \mathrm{AC}=6 \mathrm{~cm}$
Có góc đối diện với cạnh $\mathrm{AB}$ là góc $\mathrm{C}$, góc $\mathrm{A}$ đối diện với cạnh $\mathrm{BC}$, góc $\mathrm{B}$ đối diện với cạnh $\mathrm{AC}$ Theo định lí về góc đối diện với cạnh lớn hơn thì lớn hơn ta có :
$$\Rightarrow \widehat{A}>\widehat{B}>\widehat{C}$$
b)
Vì $\widehat{A}=\widehat{C}$ nên tam giác $A B C$ cân tại $B$
$$\Rightarrow B A=B C$$
Áp dụng định lí tổng 3 góc trong tam giác $\mathrm{ABC}$, có:
$$\begin{aligned}& \Rightarrow \widehat{B}=180^{\circ}-100^{\circ}=80^{\circ} \\& \Rightarrow \widehat{B}>\widehat{A}=\widehat{C}\end{aligned}$$
$\Rightarrow A C$ là cạnh lớn nhất tam giác $\mathrm{ABC}$ (Quan hệ giữa góc và cạnh đối diện trong tam giác)
Bài 2 trang 66
a) Tìm cạnh lớn nhất của tam giác $\mathrm{ABC}$.
b) Tam giác $\mathrm{ABC}$ là tam giác gì? Vì sao?
– Sử dụng định lí quan hệ cạnh và góc đối diện trong tam giác.
– Sử dụng dấu hiệu nhận biêt tam giác cân.
a) Do $\widehat{A}=100^{\circ}>90^{\circ}$ nên là góc tù, do đó, $\widehat{A}$ là góc lớn nhất trong tam giác $A B C$.
$\Rightarrow \mathrm{BC}$ là cạnh lớn nhất của tam giác $\mathrm{ABC}$ (do $\mathrm{BC}$ đối diện với góc $\mathrm{A}$ trong tam giác $\mathrm{ABC}$ )
b)
Theo định lí tổng 3 góc trong tam giác ABC, ta có:
$$\begin{aligned}& \Rightarrow \widehat{A}+\widehat{B}+\widehat{C}=180^{\circ} \\& \Rightarrow \widehat{C}=180^{\circ}-100^{\circ}-40^{\circ}=40^{\circ} \\& \Rightarrow \widehat{C}=\widehat{B}=40^{\circ}\end{aligned}$$
$\Rightarrow$ ABC là tam giác cân tại A.
Bài 3 trang 66
a) So sánh các cạnh của tam giác $\mathrm{ABC}$.
b) Lấy điểm $\mathrm{K}$ bất kì thuộc đoạn thẳng $\mathrm{AC}$. So sánh độ dài $B K$ và $B C$.
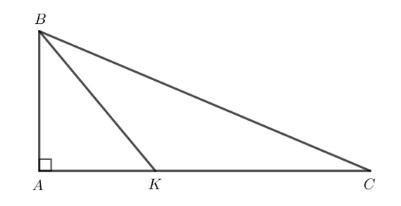
a) Tam giác ABC vuông tại A nên $\widehat{B}+\widehat{C}=90^{\circ}$ (trong tam giác vuông, tổng hai góc nhọn bằng $90^{\circ}$ ) và $\widehat{A}=90^{\circ}$ là góc lớn nhất trong tam giác $\mathrm{ABC}$.
Do $\widehat{B}>45^{\circ}=\frac{90^{\circ}}{2}$ nên $\widehat{C}\widehat{C}$.
Khi đó $\widehat{A}>\widehat{B}>\widehat{C}$.
Do đó $B C>C A>A B$.
b) Ta có: $\widehat{B K C}+\widehat{B K A}=180^{\circ}$ ( 2 góc kề bù) nên $\widehat{B K C}=180^{\circ}-\widehat{B K A}$.
$\widehat{B K A}+\widehat{B A K}+\widehat{A B K}=180^{\circ}$ (tổng 3 góc trong tam giác ABK).
Suy ra $\widehat{B A K}+\widehat{A B K}=180^{\circ}-\widehat{B K A}$.
Do đó $\widehat{B K C}=\widehat{B A K}+\widehat{A B K}=90^{\circ}+\widehat{A B K}>90^{\circ}$.
Khi đó $\widehat{B K C}$ là góc tù.
Tam giác BKC có $\widehat{B K C}$ là góc tù nên $\widehat{B K C}$ là góc lớn nhất trong tam giác BKC.
Khi đó BC là cạnh lớn nhất trong tam giác BKC.
Do đó $\mathrm{BK}<\mathrm{BC}$.
Bài 4 trang 66
a) Tìm đoạn ngắn nhất trong các đoạn $BA, BM, BC$.
b) Tìm đoạn ngắn nhất trong các đoạn $MA, MN, MB$.
c) Chứng minh rằng $MA \lt BC$.
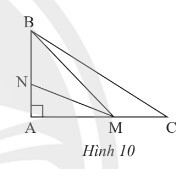
– Dựa vào tính chất từ 1 điểm ngoài đường thẳng thì đường vuông góc ngắn hơn các đường xiên .
– Ta chứng minh $\mathrm{MA}<\mathrm{AC}<\mathrm{BC}$
a) $BA$ là đường vuông góc;
$\mathrm{BM}$ và $\mathrm{BC}$ là các đường xiên kẻ từ $\mathrm{B}$ đến đường thẳng $\mathrm{AC}$
Ta được đường ngắn nhất là đường thẳng vuông góc nên $BA$ là đoạn ngắn nhất.
b) Tương tự câu a
$MA$ là đường vuông góc;
$MN$ và $\mathrm{MB}$ là các đường xiên kẻ từ $M$ đến đường thẳng $\mathrm{AB}$
Ta được đường ngắn nhất là đường thẳng vuông góc nên MA là đoạn ngắn nhất.
c) Xét tam giác $ABC$ vuông tại $A$
$\Rightarrow \widehat{A}=90^{\circ} \Rightarrow \mathrm{A}$ là góc lớn nhất tam giác $\mathrm{ABC}$
$\Rightarrow B C>A C$ ( định lí về góc đối diện và cạnh )
Vì $\mathrm{M}$ nằm giữa $\mathrm{AC}$ nên $\mathrm{AM}<\mathrm{AC}$
$\Rightarrow \mathrm{AM}<\mathrm{AC}<\mathrm{BC}$
Vậy $AM \lt BC$
Bài 5 trang 66
a) Một thanh nẹp gỗ có hai cạnh song song (Hình 11b). Chiều rộng của thanh nẹp gỗ là khoảng cách giữa hai cạnh đó. Hãy cho biết có phải chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này dến một điểm trên cạnh kia không.
b) Muốn đo chiều rộng của thanh nẹp, ta phải đặt thước như thế nào ? Vì sao?
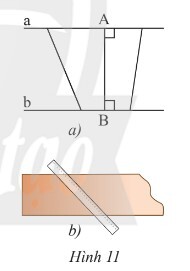
Sử dụng mối quan hệ giữa đường vuông góc và đường xiên.
a) Chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này đến một điểm trên cạnh kia (đoạn vuông góc là đoạn ngắn nhất )
b) Ta đặt thước vuông góc với 2 cạnh của nẹp vì chiều rộng của thanh nẹp là khoảng cách giữa 2 cạnh của nẹp
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Đường vuông góc và đường xiên Chương Tam giác Toán 7 Chân trời sáng tạo tập 2 ở các trang 64, 65, 66. Hi vọng các bạn sẽ có một buổi thú vị và học được nhiều điều bổ ích. Chúc các bạn học tốt!




