Giải SGK bài 7 trang 73, 74, 75, 76 chương 8 Toán 7 Chân trời sáng tạo tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Tính chất ba đường trung tuyến của tam giác. Các bài tập sau đây thuộc bài 7 chương 8 – Tam giác trang 73, 74, 75, 76 Toán 7 Chân trời sáng tạo tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Tính chất ba đường trung tuyến của tam giác
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 73, 74, 75 trong bài Tính chất ba đường trung tuyến của tam giác. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 73
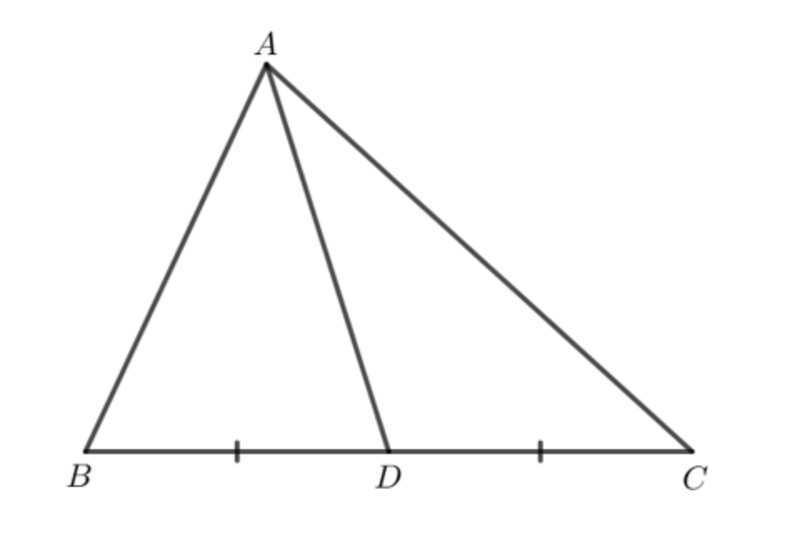
Thực hành 1 trang 73
Xác định các trung điểm của các cạnh tam giác và vẽ các đường trung tuyến.
Xác định trung điểm E của AC và trung điểm F của AB.
Nối BE và CF ta được hai đường trung tuyến còn lại của tam giác ABC.
Ta có hình vẽ sau:
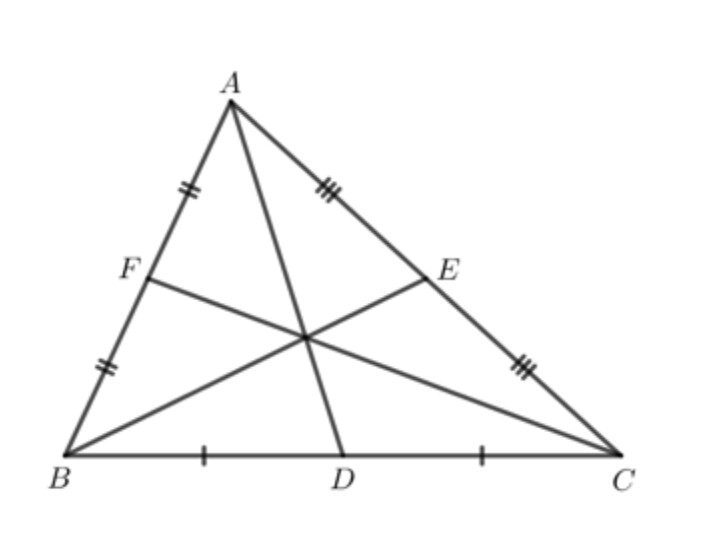
Vận dụng 1 trang 73
b) Vẽ đường trung tuyến MK của tam giác MNP (Hình 3).
c) Vẽ tam giác nhọn IJK và tất cả các đường trung tuyến của nó.
Xác định các trung điểm và vẽ các trung tuyến.
a) Tam giác DEF có đường trung tuyến DH nên H là trung điểm của EF.
Ta có hình vẽ sau:
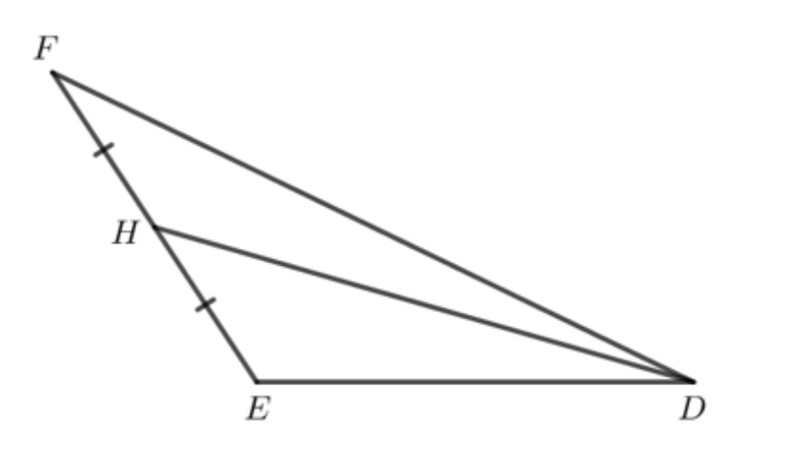
b) Tam giác vuông MNP có đường trung tuyến MK nên K là trung điểm của NP.
Ta có hình vẽ sau:
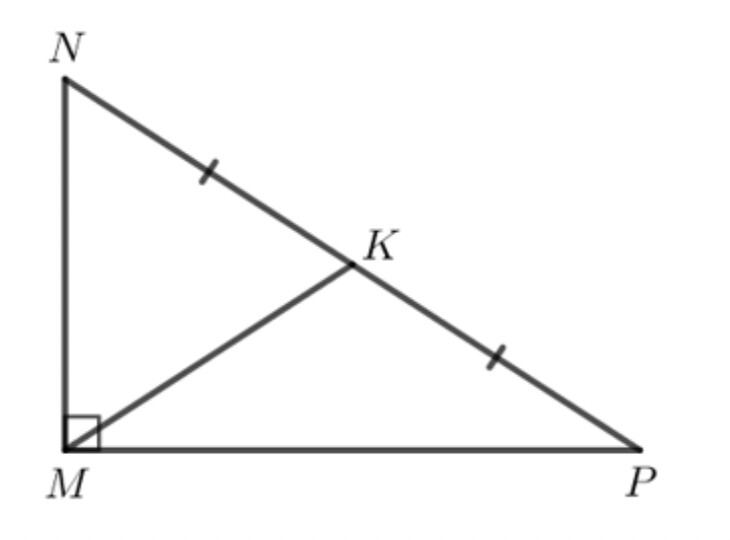 c) Gọi D, E, F lần lượt là trung điểm của các cạnh JK, KI, IJ.
c) Gọi D, E, F lần lượt là trung điểm của các cạnh JK, KI, IJ.Nối ID, JE, KF ta được ba đường trung tuyến của tam giác MNP.
Ta có hình vẽ sau:
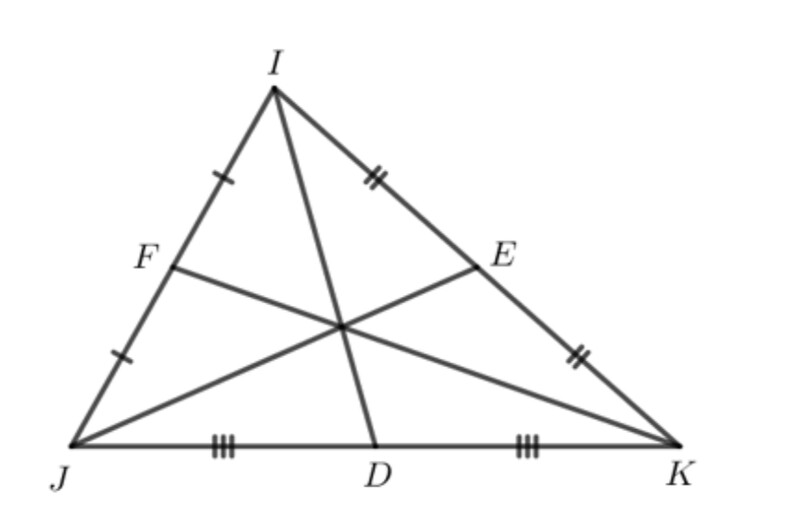
Hoạt động 2 trang 74
Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không.
b) Em hãy đếm ô rồi vẽ lại tam giác $A B C$ trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến $B E$ và $C F$ của tam giác $A B C$. Hai đường trung tuyến này cắt nhau tại G. Tia AG cắt BC tại $D$.
Em hãy quan sát vào cho biết:
– AD có phải đường trung tuyến của tam giác $A B C$ hay không?
– Các tỉ số $\frac{B G}{B E}, \frac{C G}{C F}, \frac{A G}{A D}$ bằng bao nhiêu ?
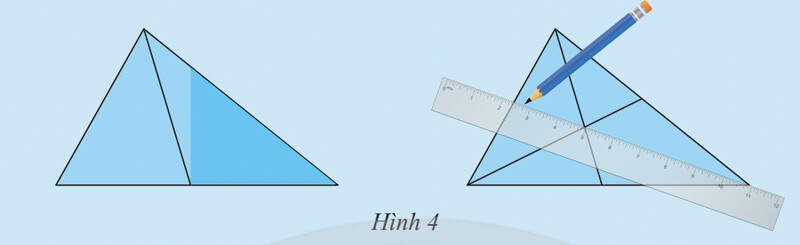
a)- Ta xác định trung điểm 1 cạnh bằng cách gấp sao cho 2 đỉnh của tam giác trùng nhau, khi đó giao của nét gấp đi qua 1 cạnh của tam giác sẽ là trung điểm của cạnh đó
– Rồi từ các trung điểm vừa xác định được ta kẻ các đường trung tuyến của tam giác từ các đỉnh
– Nhận xét : Ta thấy 3 đường trung tuyến trong tam giác này đều sẽ đi qua 1 điểm
b)
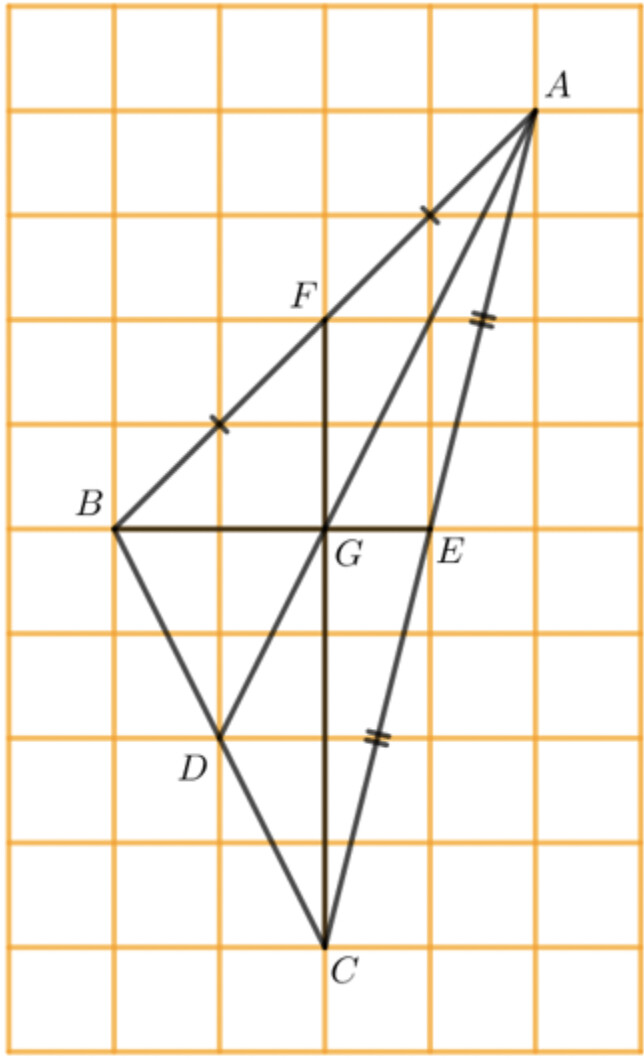
– Ta nối dài đoạn $A G$ sao cho $A G$ cắt $B C$ tại 1 điểm
– Ta thấy điểm giao nhau giữa $A G$ và $B C$ chính là trung điểm của $B C$
– Nên $A G$ là trung tuyến của tam giác $A B C$
– Ta sẽ sử dụng số đo dựa trên các ô để xét tỉ số giữa các đoạn thẳng
$\frac{B G}{B E}=\frac{2}{3} ; \frac{C G}{C F}=\frac{4}{6} ; \frac{A G}{A D}=\frac{4.4}{6.6}$
– Ta thấy sau khi rút gọn các tỉ số ta có :
$\frac{B G}{B E}=\frac{C G}{C F}=\frac{A G}{A D}=\frac{2}{3}$
Thực hành 2 trang 75
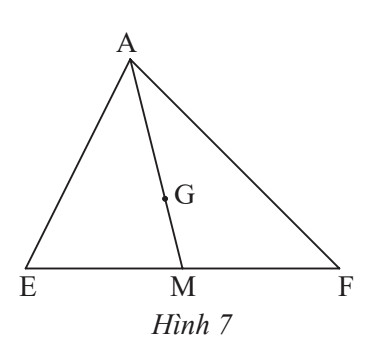
Hãy tính các tỉ số:
a) $\frac{G M}{A M}$
b) $\frac{G M}{A G}$
c) $\frac{A G}{G M}$
Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài trung tuyến đi qua đỉnh ấy
a) Vì G là trọng tâm của tam giác AEF với đường trung tuyến AM nên theo định lí 3 đường trung tuyến cắt nhau tại trọng tâm ta có :
$ \frac{A G}{A M}=\frac{2}{3} \Rightarrow \frac{G M}{A M}=1-\frac{2}{3}=\frac{1}{3} $
$\text { b) vi } \frac{A G}{A M}=\frac{2}{3} $ và $ \frac{G M}{A M}=\frac{1}{3} $ (theo câu a)
$ \Rightarrow \frac{G M}{A G}=\frac{1}{2} $
c) Vì $\frac{G M}{A G}=\frac{1}{2}$(chứng minh b)
$ \Rightarrow \frac{A G}{G M}=2$
Vận dụng 2 trang 75
– Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng$\frac{2}{3}$ độ dài trung tuyến đi qua đỉnh ấy .
– Ta sẽ chứng minh AI = IJ = JD = $\frac{2}{3}AO = \frac{2}{3}OD$
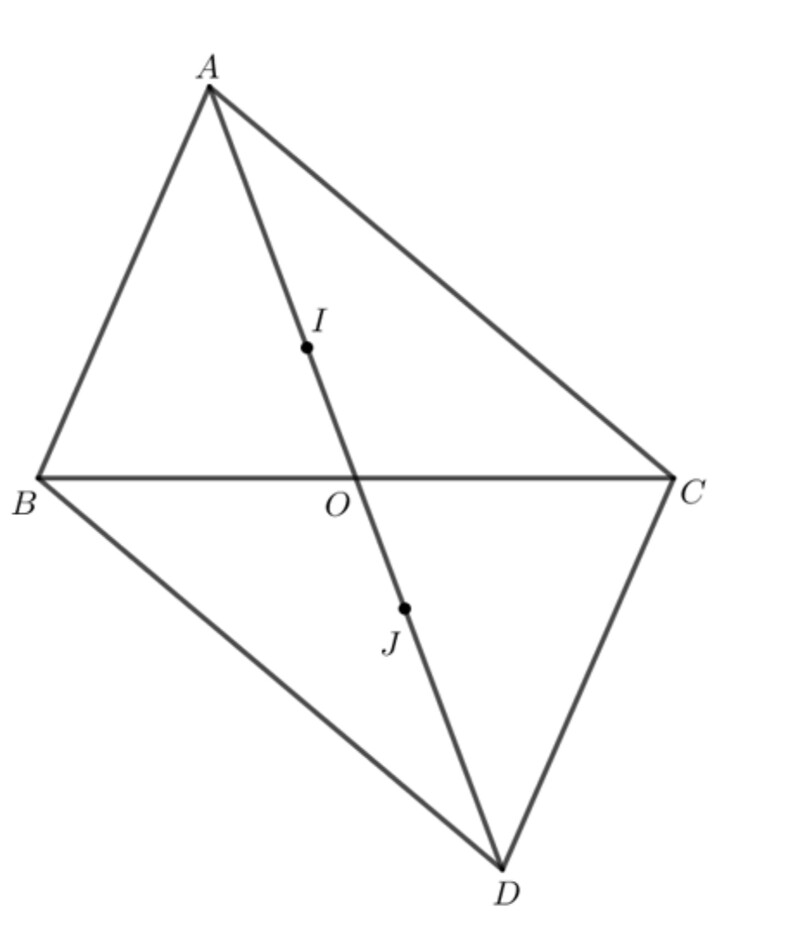
Vì l là trọng tâm tam giác $A B C$ theo giả thiết nên ta có:
$A I=\frac{2}{3} A O=2 I O$ (định lí về trọng tâm trong tam giác)
Tương tự J là trọng tâm tam giác BCD nên ta có :
$D J=\frac{2}{3} O D=2 O J$ (định lí về trọng tâm trong tam giác)
Mà OA = OD (giả thiết)
$\Rightarrow A I=D J=\frac{2}{3} O A=\frac{2}{3} O D=2 O I=2 O J$
Mà $\mathrm{OI}=\mathrm{OJ}$ do cùng $=\frac{1}{3} O A=\frac{1}{3} O D$ (tính chất trọng tâm trong tam giác)
$\Rightarrow 2 O I=2 O J=2 \frac{1}{3} A O=2 \frac{1}{3} O D=I J $
$ \Rightarrow A I=D J=I J=\frac{2}{3} O A=\frac{2}{3} O D $ (điều phải chứng minh)
Giải bài tập SGK bài Tính chất ba đường trung tuyến của tam giác
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Tính chất ba đường trung tuyến của tam giác trang 75, 76 sách Toán 7 chân trời sáng tạo tập 2 dưới đây nhé!
Bài tập 1 trang 75
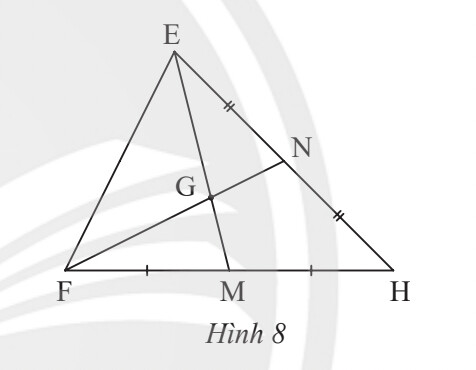
$EG = ? EM$;
$GM = ? EM$;
$GM = ? EG$;
$FG = ? GN$;
$FN = ? GN$;
$FN = ? FG$.
– Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài trung tuyến đi qua đỉnh ấy .
$ E G=\frac{2}{3} E M ; \quad G M=\frac{1}{3} E M ; \quad G M=\frac{1}{2} E G$
$ F G=2 G N ; \quad F N=3 G N ; \quad F N=\frac{3}{2} F G$
Bài tập 2 trang 75
a) Biết AM = 15 cm, tính AG
b) Biết GN = 6 cm, tính CN
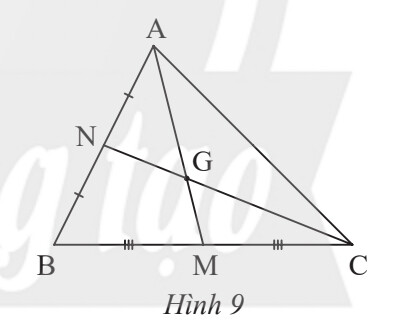
– Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài trung tuyến đi qua đỉnh ấy
– Ta áp dụng các tỉ lệ giữa các đoạn thẳng và độ dài của chúng
a) Theo đề bài ta có $A M=15 \mathrm{~cm}$
Mà $C N$ và $A M$ là 2 trung tuyến của tam giác $A B C$
AM cắt $C N$ tại $G$ nên $G$ là trọng tâm tam giác $A B C$
$\Rightarrow A G=\frac{2}{3} A M$ (định lí về trọng tâm tam giác)
$\Rightarrow A G=\frac{2}{3} 15 \mathrm{~cm}=10 \mathrm{~cm}$
b) Vì G là trọng tâm tam giác $A B C$
$\Rightarrow C G=\frac{2}{3} C N$ (theo tính chất của trung tuyến đi qua trọng tâm)
Mà $C G+G N=C N$ nên ta có $G N=C N-C G=C N-\frac{2}{3} C N=\frac{1}{3} C N$
Theo giả thiết $\mathrm{GN}=6 \mathrm{~cm}$ ta có
$\Rightarrow C N=3 G N=3.6 \mathrm{~cm}=18 \mathrm{~cm}$
Bài tập 3 trang 75
a) Chứng minh rằng BG song song với EC.
b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI
– Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài trung tuyến đi qua đỉnh ấy
– Câu a ta sẽ chứng minh 2 góc so le trong bằng nhau thông qua các tam giác bằng nhau
– Câu b ta sẽ chứng minh F là trọng tâm tam giác ABE
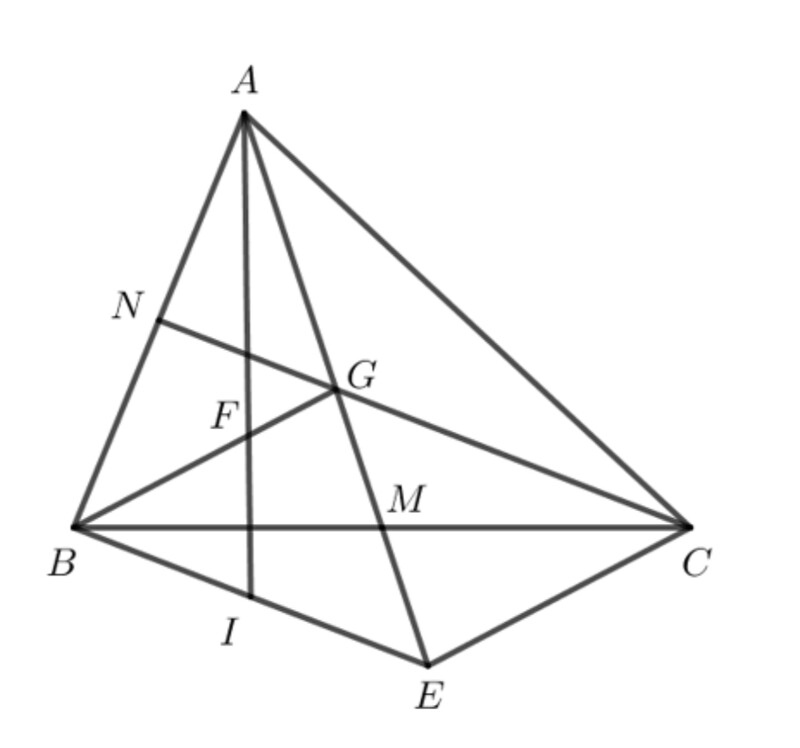
a) Xét tam giác BGM và tam giác $C E M$ có :
$\widehat{G M B}=\widehat{E M C}(2$ góc đối đỉnh)
$\mathrm{GM}=\mathrm{ME}$ (do $\mathrm{G}$ đối xứng $\mathrm{E}$ qua $\mathrm{M}$ )
$\mathrm{MB}=\mathrm{MC}$ (do $\mathrm{M}$ là trung điểm của $\mathrm{BC}$ )
$\Rightarrow \Delta B G M=\Delta C E M(c-g-c)$
$\Rightarrow \widehat{G B M}=\widehat{M C E}$ (2 góc tương ứng bằng nhau)
Mà 2 góc trên ở vị trí so le trong nên $\mathrm{BG} // \mathrm{CE}$
b) Vî I là trung điểm $\mathrm{BE}$ nên $\mathrm{Al}$ sẽ là trung tuyến của tam giác $A B E$
Và $B G$ cũng là trung tuyến của tam giác $A B E$ do $G$ là trung điểm $A E$
Vì BG cắt $\mathrm{Al}$ tại $\mathrm{F}$ nên $\mathrm{F}$ sẽ là trọng tâm của tam giác $A B E$
$\Rightarrow A F=\frac{2}{3} A I$ (định lí về trọng tâm tam giác)
$\mathrm{Mà} \mathrm{Al}=\mathrm{AF}+\mathrm{FI} \Rightarrow \mathrm{FI}=\mathrm{Al}-\mathrm{AF}$
$\Rightarrow F I=A I-\frac{2}{3} A I=\frac{1}{3} A I$
$\Rightarrow 2 F I=A F=\frac{2}{3} A I$
$\Rightarrow \mathrm{AF}=2 \mathrm{Fl}$
Bài tập 4 trang 75
a) Chứng minh rằng BM = CN
b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC
– Ta chứng minh 2 tam giác bằng nhau để từ đó chứng minh 2 đoạn thẳng bằng nhau
– Ta chứng minh I là trọng tâm tam giác ABC và chứng minh AH là trung tuyến của tam giác ABC và H là trung điểm của BC
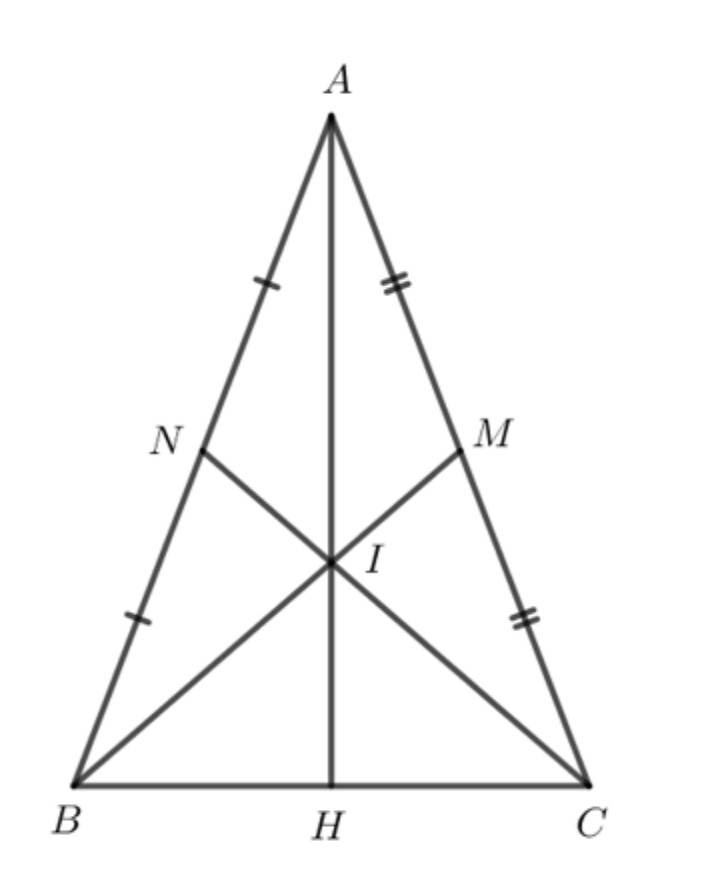
a) Vì tam giác $A B C$ cân tại $A$ theo giả thiết.
$B M$ và $C N$ là 2 đường trung tuyến nên $M, N$ là 2 trung điểm của $A C, A B$.
Vì $A B=A C$ (tính chất tam giác cân)
$\Rightarrow \frac{A B}{2}=\frac{A C}{2}=A N=A M$
Xét tam giác $\mathrm{AMB}$ và tam giác ANC ta có :
$\mathrm{AM}=\mathrm{AN}$ (cmt)
$\mathrm{AB}=\mathrm{AC} $
Góc $\mathrm{A}$ chung
$ \Rightarrow \Delta A M B=\Delta A N C $
$ \Rightarrow B M=C N$ ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của $\mathrm{BM}$ và $\mathrm{CN}$
$\Rightarrow$ I là trọng tâm của tam giác $A B C$
$\Rightarrow \mathrm{AI}$ là đường trung tuyến của tam giác $\mathrm{ABC}$ hay $\mathrm{AH}$ đường là trung tuyến của tam giác $\mathrm{ABC}$
$\Rightarrow \mathrm{H}$ là trung điểm của $B C$
Bài tập 5 trang 76
– Ta chứng minh AB = AC bằng cách chứng minh 2 tam giác bằng nhau.
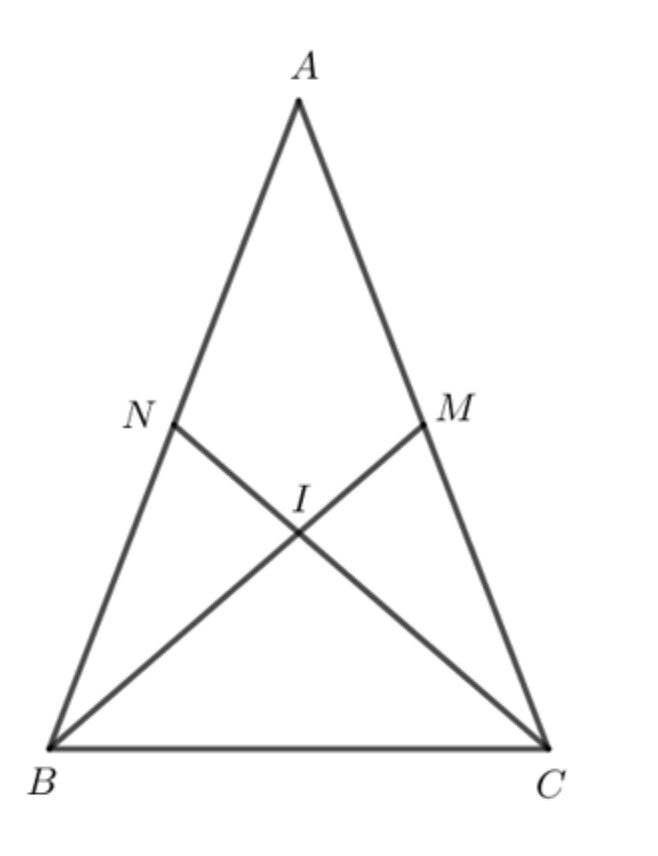
Gọi $\mathrm{D}$ là giao điểm của $\mathrm{CN}$ và $\mathrm{BM}$
$\Rightarrow D$ là trọng tâm tam giác $A B C$
$ \Rightarrow C D=\frac{2}{3} C N=B D=\frac{2}{3} B M$( do $ \mathrm{BM}=\mathrm{CN}$)
$ \Rightarrow$ Tam giác $\mathrm{DBC} $ cân tại $ \mathrm{D} $do$ \mathrm{BD}=\mathrm{CD} $
$ \Rightarrow \widehat{D B C}=\widehat{D C B} $ (2 góc đáy trong tam giác cân) (1)
Xét $\triangle N D B$ và $\triangle M D C$ có :
$B D=C D$
$\widehat{N D B}=\widehat{M D C}$ ( 2 góc đối đỉnh)
$\mathrm{ND}=\mathrm{DM}$ (do cùng $=\frac{1}{3} C N=\frac{1}{3} B M$ (tính chất của trung trực đi qua trọng tâm tam giác)
$ \Rightarrow \Delta N D B=\Delta M D C $(c.g.c)
$ \Rightarrow \widehat{N B D}=\widehat{M C D}$ (2 góc tương ứng) (2)
Từ (1) và (2) $ \Rightarrow \widehat{A B C}=\widehat{A C B} $
Do $ \widehat{A B C}=\widehat{N B D}+\widehat{D B C} \text { và } \widehat{A C B}=\widehat{M C D}+\widehat{D C B} $
$ \Rightarrow \Delta A B C$ cân tại $ \mathrm{A} $ (do 2 góc bằng nhau)
Bài tập 6 trang 76
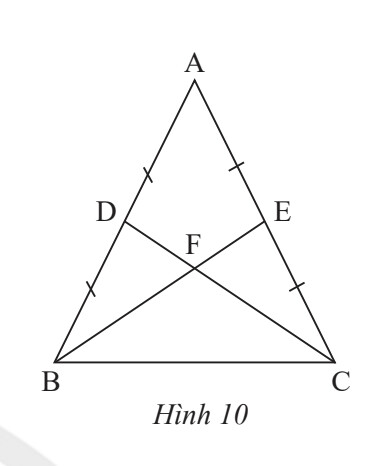
– Ta chứng minh F là trọng tâm tam giác ABC
– Sau đó chứng minh CD = BE
– Áp dụng định lí về trọng tâm tam giác ta tính các đoạn DF, EF
Vì $\mathrm{BE}, \mathrm{CD}$ là 2 trung tuyến của tam giác $\mathrm{ABC}$
Nên $E, D$ lần lượt là trung tuyến của $A B$ và $A C$
$\Rightarrow A D=A E=\frac{1}{2} A B=\frac{1}{2} A C$
Xét tam giác ADC và tam giác AEB có :
$A D=A E$
Góc A chung
$\mathrm{AB}=\mathrm{AC}$ (tam giác $A B C$ cân tại $A$ theo giả thiết)
$\Rightarrow \triangle A D C=\triangle A E B(c-g-c)$
$\Rightarrow B E=C D$ (cạnh tương ứng)
Vì F là giao 2 trung tuyến nên $F$ là trọng tâm tam giác $A B C$
$\Rightarrow C F=B F=\frac{2}{3} B E=\frac{2}{3} C D$ ( định lí về trung tuyến đi qua trọng tâm tam giác)
$\Rightarrow \frac{1}{3} B E=\frac{1}{3} C D \Rightarrow D F=F E=\frac{1}{3} .9 \mathrm{~cm}=3 \mathrm{~cm}$
$\Rightarrow D F=3 \mathrm{~cm}$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 7 chương 8 – Tam giác trang 73, 74, 75, 76 Toán 7 Chân trời sáng tạo tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!




