Giải SGK bài Tập hợp Q các số hữu tỉ chương 1 Toán 7 Cánh diều tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Tập hợp Q các số hữu tỉ. Các bài tập sau đây thuộc bài 1 chương 1 – Số hữu tỉ trang 5, 6, 7, 8, 9, 10, 11 Toán 7 Cánh diều tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Tập hợp Q các số hữu tỉ
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 5, 6, 7, 8, 9, 10 trong bài Tập hợp Q các số hữu tỉ. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi khởi động trang 5

Các chỉ số nhiệt độ nêu ở trên có được viết dưới dạng phân số không?
Viết số thập phân dưới dạng phân số có mẫu số là lũy thừa của 10 như đã học.
Các số chỉ nhiệt độ nêu trên có viết được dưới dạng phân số. Cụ thể:
$-1,3=\frac{-13}{10} ;-0,5=\frac{-5}{10}=\frac{-1}{2} $
$ 0,3=\frac{3}{10} ;-3,1=\frac{-31}{10}$
Hoạt động 1 trang 5
Biểu diễn số nguyên a dưới dạng phân số $\frac{a}{1}$
Số thập phân dưới dạng phân số có mẫu số là lũy thừa của 10.
Hỗn số dương $a \frac{b}{c}=\frac{a . c+b}{c}$
$-3=\frac{-3}{1}$
$ 0,5=\frac{5}{10}=\frac{1}{2} $
$2 \frac{3}{7}=\frac{2.7+3}{7}=\frac{17}{7}$
Luyện tập vận dụng 1 trang 6
Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}(a, b \in Z, b \neq 0)$.
Các số $21 ;-12 ; \frac{-7}{-9} ;-4,7 ;-3,05$ có là số hữu tỉ vì chúng đều viết được dưới dạng phân số $21=\frac{21}{1} ;-12=\frac{-12}{1} ; \frac{-7}{-9}=\frac{7}{9} ;-4,7=\frac{-47}{10} ;-3,05=\frac{-305}{100}=\frac{-61}{20}$
Hoạt động 2 trang 6
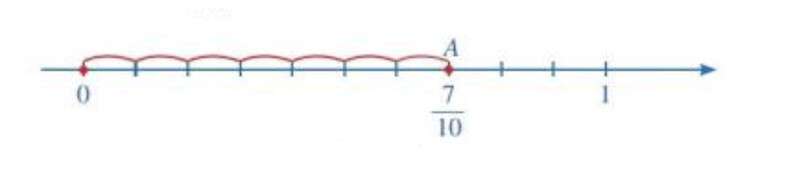
Chia đoạn thẳng đơn vị thành 10 phần bằng nhau. Lấy một đoạn làm đơn vị mới ( đơn vị mới bằng $\frac{1}{10}$ đơn vị cũ)
Số hữu tỉ $\frac{7}{10}$ được biểu diễn bằng điểm nằm bên phải gốc $\mathrm{O}$, cách gốc $\mathrm{O}$ một đoạn bằng 7 đơn vị mới.
Luyện tập vận dụng 2 trang 7
Viết các số hữu tỉ dưới dạng phân số: -0,3 = – $\frac{3}{10}$
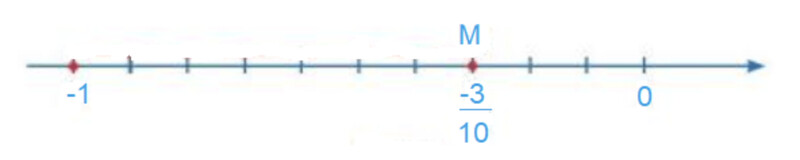
Chia đoạn thẳng đơn vị thành 10 phần bằng nhau. Lấy một đoạn làm đơn vị mới ( đơn vị mới bằng $\frac{1}{10}$ đơn vị cũ).
Số hữu tỉ – $\frac{3}{10}$ được biểu diễn bằng điểm nằm bên trái gốc $\mathrm{O}$, cách gốc $\mathrm{O}$ một đoạn bằng 3 đơn vị mới.
Hoạt động 3 trang 7
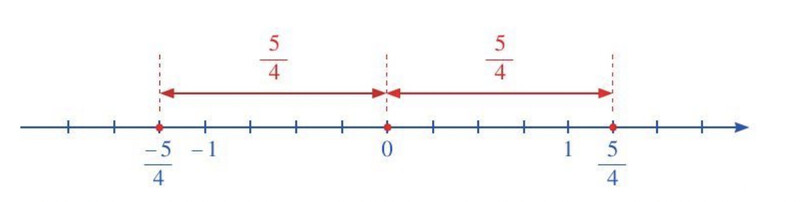
Nêu nhận xét về khoảng cách từ hai điểm $\frac{5}{4}$ và $\frac{-5}{4}$ đến điểm 0.
So sánh khoảng cách từ hai điểm $\frac{5}{4}$ và $\frac{-5}{4}$ đến điểm 0.
Hai điểm biểu diễn các số hữu tỉ $\frac{5}{4}$ và $\frac{-5}{4}$ cách gốc 0 một khoảng bằng nhau.
Luyện tập vận dụng 3 trang 8
Số đối của số hữu tỉ $\frac{a}{b}$ là số hữu tỉ $\frac{-a}{b}$.
Số đối của $\frac{2}{9}$ là – $\frac{2}{9}$
Số đối của $-0,5$ là 0,5
Hoạt động 4 trang 8
a) $-\frac{1}{3}$ và $\frac{-2}{5}$
b) 0,125 và 0,13
c) $-0,6$ và $\frac{-2}{3}$
a) Đưa 2 phân số về dạng cùng mẫu số dương rồi so sánh tử số của 2 phân số: Phân số nào có tử số lớn hơn thì lớn hơn
b) So sánh 2 số thập phân: So sánh các hàng tương ứng từ trái qua phải của 2 số thập phân
c) Viết chúng dưới dạng phân số rồi so sánh 2 phân số.
a) Ta có:
$-\frac{1}{3}=\frac{-5}{15} ; \frac{-2}{5}=\frac{-6}{15}$
Vì $-5>-6$ nên $\frac{-5}{15}>\frac{-6}{15}$ hay $-\frac{1}{3}>\frac{-2}{5}$
b) $0,125-10 \text { nên } \frac{-9}{15}>\frac{-10}{15} \text { hay }-0,6>\frac{-2}{3}$
Luyện tập vận dụng 4 trang 9
a) $-3,23$ và $-3,32$
b) $-\frac{7}{3}$ và $-1,25$
a) So sánh 2 số thập phân dương: So sánh các hàng tương ứng từ trái qua phải của 2 số thập phân
Nếu $a>b$ thì $-a<-b$.
b) Viết chúng dưới dạng phân số rồi so sánh 2 phân số.
a) Ta có: 3,23 -3,32
b) Ta có: $-\frac{7}{3}=\frac{-28}{12} ;-1,25=\frac{-125}{100}=\frac{-5}{4}=\frac{-15}{12}$
Vì $-28<-15$ nên $\frac{-28}{12}<\frac{-15}{12}$ hay $-\frac{7}{3}<-1,25$
Hoạt động 5 trang 10
Biểu diễn 2 số nguyên trên trục số nằm ngang.
Nếu a < b thì điểm a nằm bên trái điểm b trên trục số.
Nhận xét: Trên trục số nằm ngang, điểm biểu diễn số hữu tỉ nhỏ hơn nằm bên trái điểm biểu diễn số hữu tỉ lớn hơn.
Giải bài tập SGK bài Tập hợp Q các số hữu tỉ
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Tập hợp Q các số hữu tỉ trang 10, 11 sách Toán 7 Cánh diều tập 1 dưới đây nhé!
Bài tập 1 trang 10
Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}(a, b \in Z, b \neq 0)$
Các số $13,-29 ;-2,1 ; 2,28 ; \frac{-12}{-18}$ có là số hữu tỉ vì:
$13=\frac{13}{1} ;-29=\frac{-29}{1} ;-2,1=\frac{-21}{10}$
$ 2,28=\frac{228}{100}=\frac{54}{25} ; \frac{-12}{-18}=\frac{2}{3}$
Bài tập 2 trang 10
a) $21 ? \mathbb{Q}$;
c) $\frac{5}{-7} ? \mathbb{Z}$;
d) $0 ? \mathbb{Q}$
e) $-7,3 ? \mathbb{Q}$;
g) $3 \frac{2}{9} ? \mathbb{Q}$.
Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}(a, b \in Z, b \neq 0)$
Dùng kí hiệu ” $\in$ ” nếu số thuộc tập hợp
Dùng kí hiệu ” $\notin$ ” nếu số không thuộc tập hợp
a) $21 \in \mathrm{Q}$
b) $-7 \notin N$
c) $\frac{-5}{7} \notin \mathrm{Z}$
d) $0 \in \mathrm{Q}$
e) $-7,3 \in$ Q
g) $3 \frac{2}{9} \in \mathrm{Q}$
Bài tập 3 trang 10
a) Nếu $a \in \mathbb{N}$ thì $a \in \mathbb{Q}$
b) Nếu $a \in \mathbb{Z}$ thì $a \in \mathbb{Q}$
c) Nếu $a \in \mathbb{Q}$ thì $a \in \mathbb{N}$
d) Nếu $a \in \mathbb{Q}$ thì $a \in \mathbb{Z}$
e) Nếu $a \in \mathbb{N}$ thì $a \notin \mathbb{Q}$
g) Nếu $a \in \mathbb{Z}$ thì $a \notin \mathbb{Q}$
Tập hợp các số hữu tỉ $ \mathbb{Q}=\left\{\frac{a}{b} ; a, b \in \mathbb{Z} ; b \neq 0\right\} $
$ \mathbb{N}=\{0 ; 1 ; 2 ; \ldots\} $
$ \mathbb{Z}=\{\ldots,-2 ;-1 ; 0 ; 1 ; 2 ; \ldots\}$
a) Nếu $a \in \mathbb{N}$ thì $a \in \mathbb{Q}=>$ Đúng
b) Nếu $a \in \mathbb{Z}$ thì $a \in \mathbb{Q}$ => Đúng
c) Nếu $a \in \mathbb{Q}$ thì $a \in \mathbb{N}=>$ Sai. Vì a là số hữu tỉ thì chưa chắc a là số tự nhiên.
d) Nếu $a \in \mathbb{Q}$ thì $a \in \mathbb{Z}=>$ Sai. Vì a là số hữu tỉ thì chưa chắc a là số nguyên.
e) Nếu $a \in \mathbb{N}$ thì $a \notin \mathbb{Q}=>$ Sai. Vì các số tự nhiên là các số hữu tỉ
g) Nếu $a \in \mathbb{Z}$ thì $a \notin \mathbb{Q}=>$ Sai. Vì các số nguyên là các số hữu tỉ
Bài tập 4 trang 11

Điểm biểu diễn số hữu tỉ a là điểm a.
Quan vị trí các điểm A, B, C, D trên trục số và trả lời câu hỏi.
Các điểm A, B, C, D biểu diễn lần lượt các số: $-\frac{9}{7} ;-\frac{3}{7} ; \frac{2}{7} ; \frac{6}{7}$
Bài tập 5 trang 11
Số đối của số x kí hiệu là: -x
Số đối của các số $\frac{9}{25} ; \frac{-8}{27} ;-\frac{15}{31} ; \frac{5}{-6} ; 3,9 ;-12,5$
lần lượt là: $-\frac{9}{25} ; \frac{8}{27} ; \frac{15}{31} ; \frac{5}{6} ;-3,9 ; 12,5$.
Bài tập 6 trang 11

Số đối của một số a nằm bên kia số 0 và cách 0 một khoảng bằng với khoảng cách từ điểm a đến điểm 0.
– Số đối của $\frac{-5}{6}$ là $\frac{5}{6}$
– Số đối của $\frac{-1}{3}$ là $\frac{1}{3}$
– Số đối của 1 là -1
– Số đối của $\frac{7}{6}$ là $\frac{-7}{6}$

Bài tập 7 trang 11
a) 2,4 và $2 \frac{3}{5}$;
b) $-0,12$ và $-\frac{2}{5}$
c) $\frac{-2}{7}$ và $-0,3$.
Đưa các số về dạng hai phân số cùng mẫu rồi so sánh.
a) $2,4=\frac{24}{10}=\frac{12}{5}$ và $2 \frac{3}{5}=\frac{13}{5}$
Ta có: $\frac{12}{5}<\frac{13}{5} \Rightarrow 2,4-10$ nên $-\frac{3}{25}>-\frac{10}{25}$ nên $-0,12>-\frac{2}{5}$.
c) $\frac{-2}{7}=\frac{-20}{70}$ và $-0,3=\frac{-3}{10}=\frac{-21}{70}$.
Do $-20>-21$ nên $\frac{-20}{70}>\frac{-21}{70}$ nên $\frac{-2}{7}>-0,3$.
Bài tập 8 trang 11
b) Sắp xếp các số sau theo thứ tự giảm dần: $\frac{-5}{6} ;-0,75 ;-4,5 ;-1$.
– Đưa các số về các phân số có cùng mẫu số để so sánh
– Sắp xếp các phân số theo thứ tự.
a) Ta có:
$ \frac{-3}{7}=\frac{-6}{14} ; \frac{-1}{2}=\frac{-7}{14} $
$\frac{2}{5}=\frac{14}{35} ; \frac{2}{7}=\frac{10}{35}$
Vì $-7\lt-6\lt0$ nên $\frac{-7}{14}\lt\frac{-6}{14}\lt0$
Vì $0\lt10\lt14$ nên $0\lt\frac{10}{35}\lt\frac{14}{35}$
Do đó: $\frac{-7}{14}\lt\frac{-6}{14}\lt\frac{10}{35}\lt\frac{14}{35}$
=> Sắp xếp các số theo thứ tự tăng dần: $\frac{-1}{2} ; \frac{-3}{7} ; \frac{2}{7} ; \frac{2}{5}$
b) Ta có: $\frac{-5}{6}=-0,8(3)$
Mà $-0,75\gt-0,8(3)\gt-1\gt-4,5$.
=>Sắp xếp các số theo thứ tự giảm dần: $-0,75 ; \frac{-5}{6} ;-1 ;-4,5$
Bài tập 9 trang 11
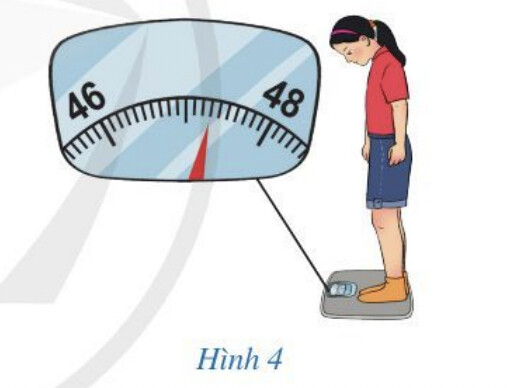
Quan sát độ chia nhỏ nhất của chiếc cân và quan sát xem chiếc kim chỉ vào số bao nhiêu.
Ta thấy độ chia nhỏ nhất là 100g, chiếc kim chỉ quá số 47 ba vạch chia nhỏ nhất nên nó chỉ số 47,3kg.
Vậy bạn Dương đọc đúng, bạn Minh và Quân đọc sai.
Bài tập 10 trang 11
Đổi chiều cao của tầng hầm ra số thập phân rồi so sánh với sáu số đo chiều cao được tư vấn.
=>Chọn chiều cao lớn hơn chiều cao của tầng hầm.
Ta có: $\frac{13}{5}=\frac{26}{10}=2,6$
Ta thấy $2,75>2,6$ nên số đo chiều cao của tầng hầm được chọn là: $2,75m$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Tập hợp Q các số hữu tỉ chương 1 –Số hữu tỉ trang 5, 6, 7, 8, 9, 10, 11 Toán 7 Cánh diều tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





