Giải SGK bài Tập hợp R các số thực chương 2 Toán 7 Cánh diều tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Tập hợp R các số thực. Các bài tập sau đây thuộc bài 2 chương 2 – Số thực trang 38, 39, 40, 41, 42 Toán 7 Cánh diều tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Tập hợp R các số thực
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 38, 39, 40, 41, 42 trong bài Tập hợp R các số thực. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 38
b) Nêu 2 ví dụ về số vô tỉ
Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}({a, b \in Z, b \neq 0)}$
Những số không phải số hữu tỉ là số vô tỉ.
a) $\frac{3}{8} ;-0,2$ là các số hữu tỉ
b) $-\sqrt{3} ; \pi$ là các số vô tỉ
Hoạt động 2 trang 38
b) Nêu biểu diễn thập phân của số vô tỉ.
Nhớ lại dạng thập phân của số hữu tỉ, số vô tỉ đã học
a) Số hữu tỉ được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn
b) Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn
Hoạt động 3 trang 39
Biểu diễn trên trục số như sau:
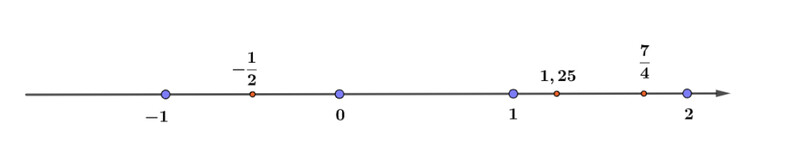
Luyện tập vận dụng 1 trang 40
$\frac{2}{-9} ;-0,5 ;-\sqrt{3}$
Số đối của số thực $a$ là $-a$
Số đối của $\frac{2}{-9} ;-0,5 ;-\sqrt{3}$ lần lượt là: $\frac{2}{9} ; 0,5 ; \sqrt{3}$
Hoạt động 5 trang 40
b) Nêu quy tắc so sánh 2 số thập phân hữu hạn.
* So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương
* So sánh 2 số thập phân dương:
Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn
Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu “,”), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn
*So sánh 2 số thập phân âm:
Nếu $a \lt b$ thì $–a \gt – b$
a) Vì $0,617 \gt 0,614$ nên $-0,617 \lt -0,614$
b) * So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương
* So sánh 2 số thập phân dương:
Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn
Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu “,”), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn
*So sánh 2 số thập phân âm:
Nếu $a \lt b$ thì $–a \gt – b$
Luyện tập vận dụng 2 trang 41
a) $1,(375)$ và $1 \frac{3}{8}$
b) $-1,(27)$ và $-1,272$
Viết các số thực dưới dạng số thập phân. Đối với các số thập phân vô hạn tuần hoàn, ta đổi dạng viết có chu kì về dạng không viết chu kì.
a) Ta có: $1,(375)=1,375375375 \ldots$
$1 \frac{3}{8}=1,375$
Vì $1,375375 … \gt1,375$ nên $1,(375)\gt1 \frac{3}{8}$
b) Ta có: $-1,(27)=-1,272727 \ldots$
Vì $1,272727… \gt1,272$ nên $- 1,272727\lt-1,272$ hay $-1,(27)\lt-1,272$
Giải bài tập SGK bài Tập hợp R các số thực
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Tập hợp R các số thực trang 42 sách Toán 7 Cánh diều tập 1 dưới đây nhé!
Bài tập 1 trang 42
a) Nếu $a \in Z$ thì $a \in R$
b) Nếu $a \in Q$ thì $a \in R$
c) Nếu $a \in R$ thì $a \in Z$
d) Nếu $a \in R$ thì $a \notin Q$
$Z$: tập hợp các số nguyên:
$Z=\{-3 ;-2 ;-1 ; 0 ; 1 ; 2 ; 3 ; . .\}$.
$Q$: tập hợp các số hữu tỉ
$R$: tập hợp các số thực
a) Đúng vì 1 số nguyên cũng là số thực
b) Đúng vì 1 số hữu tỉ cũng là số thực
c) Sai vì 1 số thực có thể không là số nguyên. Chẳng hạn, số $0,2 \in R$ nhưng $0,2 \notin Z$
d) Sai vì 1 số thực có thể là số hữu tỉ hoặc không là số hữu tỉ. Chẳng hạn $0,2 \in R$ và $0,2 \in Q$
Bài tập 2 trang 42
$\frac{-8}{35} ; \frac{5}{-6} ;-\frac{18}{7} ; 1,15 ;-21,54 ;-\sqrt{7} ; \sqrt{5}$
Số đối của số thực $a$ là $-a$
Số đối của $\frac{-8}{35} ; \frac{5}{-6} ;-\frac{18}{7} ; 1,15 ;-21,54 ;-\sqrt{7} ; \sqrt{5}$
lần lượt là: $\frac{8}{35} ; \frac{5}{6} ; \frac{18}{7} ;-1,15 ; 21,54 ; \sqrt{7} ;-\sqrt{5}$
Bài tập 3 trang 42
a) $-1,(81)$ và $-1,812$;
b) $2 \frac{1}{7}$ và 2,142 ;
d) $\sqrt{5}$ và $\sqrt{8}$
a,b,c) Viết các số thực dưới dạng số thập phân.
* So sánh 2 số thập phân dương:
Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn
Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng ( sau dấu “,”), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn
*So sánh 2 số thập phân âm:
Nếu $a \lt b$ thì $-a \gt – b$
d) Nếu $\mathrm{a}\gt\mathrm{b}\gt0$ thì $\sqrt{a}\gt\sqrt{b}$
a) Ta có: $1,(81)=1,8181 \ldots$
b) Ta có: $2 \frac{1}{7}=2,142857 \ldots$.
Vì $2,142857….\gt 2,142$ nên $2 \frac{1}{7}\gt 2,142$
d) Vì $5\lt8$ nên $\sqrt{5}\lt\sqrt{8}$
Bài tập 4 trang 42

Kết quả điền theo bảng sau:

Bài tập 5 trang 42
$-2,63…; 3,(3); -2,75…; 4,62$.
b) Sắp xếp các số sau theo thứ tự giảm dần:
$1,371…; 2,065; 2,056…; -0,078…; 1,(37)$.
* So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương
* So sánh 2 số thập phân dương:
Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn
Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu “,”), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn
*So sánh 2 số thập phân âm:
Nếu $a \lt b$ thì $–a \gt – b$
a) Ta có: $-2,63…$; $-2,75 \lt 0$;
$3,(3)$; $4,62 \gt 0$
Vì $2,63…\lt 2,75$ nên $-2,63…\gt -2,75$
Mà $3,(3) \lt 4,62$
Nên $-2,75 \lt -2,63…\lt 3,(3) \lt 4,62$
Vậy các số trên theo thứ tự tăng dần là: $-2,75 ; -2,63…; 3,(3) ; 4,62$
b) Ta có: $-0,078 \lt 0$
$1,371…; 2,065; 2,056…; 1,(37) \gt 0$
Ta có:$ 1,(37) = 1,3737….$
Ta được: $2,065 \gt 2,056…\gt 1,3737…. \gt 1,371…$
Nên $2,065 \gt 2,056…\gt 1,3737…. \gt 1,371… \gt -0,078$
Vậy các số trên theo thứ tự giảm dần là: $2,065 ; 2,056…; 1,3737…. ; 1,371… ; -0,078$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Tập hợp R các số thực chương 2 – Số thực trang 38, 39, 40, 41, 42 Toán 7 Cánh diều tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





