Giải SGK Bài 1 trang 90, 91,92,93,94 Chương 4 Toán 7 Cánh Diều Tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Góc ở vị trí đặc biệt Các bài tập sau đây thuộc bài 1 chương 4 – Góc, Đường thẳng song song trang 90, 91, 92, 93, 94 Toán 7 Cánh diều tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK Bài 1 Chương 4
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi khởi động, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 90, 91, 92, 93, 94 trong bài Góc ở vị trí đặc biệt Cùng HocThatGioi đi tìm đáp án ngay nhé!
Giải câu hỏi khởi động Trang 90 SGK Toán 7 Cánh Diều Tập 1

Hai góc đó có liên hệ gì đặc biệt?
Xác định đỉnh, cạnh của hai góc đó
2 góc được đánh dấu là 2 góc có: chung đỉnh; có chung một cạnh ; kim giờ và kim giây nằm về hai phía của kim phút.
Hoạt động 1 trang 90
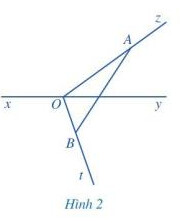
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
Vẽ hình và nhận xét
a)
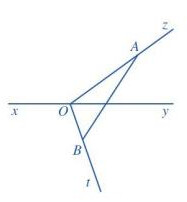
b) Đoạn thẳng AB cắt đường thẳng xy
Hoạt động 2 trang 90
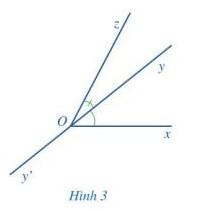
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
b) Vẽ tia đối Oy’ của tia Oy.
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy’ hay không?
Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
+ Vẽ hình và nhận xét.
a) Đỉnh của góc xOy và zOy cùng là đỉnh O; cạnh chung là cạnh Oy.
b)
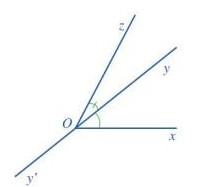
c) Hai tia Ox và Oz nằm về hai phía của đường thẳng yy’
Luyện tập vận dụng 1 trang 91
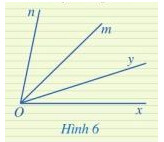
2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
Hai góc xOy và mOn không phải là hai góc kề nhau vì không có cạnh nào chung.
Luyện tập vận dụng 2 trang 92
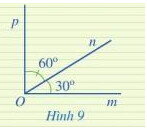
2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
Tính chất 2 góc kề nhau
Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên:
\widehat{mOn} + \widehat{nOp} = \widehat{mOp} \Longrightarrow 30^{\circ}+60^{\circ} = \widehat{mOp}
\Longrightarrow 90^{\circ} = \widehat{mOp}
Vậy \widehat{mOp} = 90^{\circ}
Hoạt động 3 trang 92
Tìm tổng số đo của góc
2 góc có tổng số đo là: 110^{\circ} + 70^{\circ} = 180^{\circ}
Hoạt động 4 trang 93
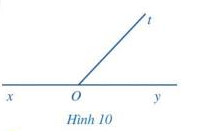
a) Hai góc xOt và yOt có kề nhau không?
b) Tính \widehat{xOt} + \widehat{yOt}
a) 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
b) Dựa vào tính chất 2 góc kề nhau, tính tổng số đo
a) Hai góc xOt và yOt là hai góc kề nhau vì có đỉnh O chung, cạnh Ot chung, 2 cạnh còn lại là Ox và Oy nằm về hai phía so với đường thẳng chứa tia Ot
b) Vì tia Ot nằm trong góc xOy nên \widehat{xOt} + \widehat{yOt} = \widehat{xOy}
Mà \widehat{xOy} = 180^{\circ} (góc bẹt)
Chú ý:
Ta có thể đo số đo 2 góc xOt và yOt rồi tính tổng của chúng
Luyện tập vận dụng 3 trang 93
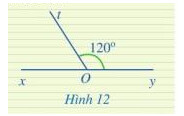
Sử dụng tính chất : Tổng số đo của 2 góc kề bù bằng 180 độ
Ta có: \widehat{xOt} + \widehat{yOt} = 180^{\circ} (2 góc kề bù)
\Longrightarrow \widehat{xOt} + 120^{\circ} = 180^{\circ}
\Longrightarrow \widehat{xOt} = 180^{\circ} – 120^{\circ} = 60^{\circ}
Hoạt động 5 trang 93
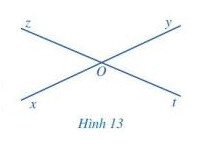
a) Cạnh Ox của góc xOz là tia đối của cạnh nào của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh nào của góc yOt.
Hai tia đối nhau nếu chúng có chung gốc và hợp thành 1 đường thẳng
a) Cạnh Ox của góc xOz là tia đối của cạnh Oy của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh Ot của góc yOt.
Hoạt động 6 trang 94
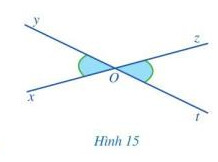
a) Hai góc xOy và yOz là hai góc kề bù;
b) Hai góc yOz và zOt là hai góc kề bù;
c) \widehat{xOy} + \widehat{yOz} = \widehat{yOz} + \widehat{zOt} \ và \widehat{xOy} = \widehat{zOt}
+ 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
+ 2 góc có tổng số đo là 180 độ là 2 góc bù nhau
+ 2 góc kề bù nếu chúng vừa kề nhau, vừa bù nhau
a) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz nằm về hai phía đối với đường thẳng chứa tia Oy nên hai góc \widehat{xOy} và \widehat{yOz} là hai góc kề nhau. Hơn nữa, hai góc \widehat{xOy} và \widehat{yOz} có tổng bằng góc \widehat{xOz} =180 độ nên hai góc \widehat{xOy} và \widehat{yOz} là hai góc bù nhau.
Vậy hai góc \widehat{xOy} và \widehat{yOz} là hai góc kề bù
Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz là hai tia đối nhau nên hai góc \widehat{xOy} và \widehat{yOz} là hai góc kề bù.
b) Cách 1: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot nằm về hai phía đối với đường thẳng chứa tia Oz nên hai góc \widehat{yOz} và \widehat{zOt} là hai góc kề nhau. Hơn nữa, hai góc \widehat{yOz} và zOt có tổng bằng góc xOz =180 độ nên hai góc yOz và zOt là hai góc bù nhau.
Vậy hai góc \widehat{yOz} và \widehat{zOt} là hai góc kề bù
Cách 2: Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot là hai tia đối nhau nên hai góc \widehat{yOz} và \widehat{zOt} là hai góc kề bù.
c) Do \widehat{xOy} + \widehat{yOz} = \widehat{xOz} = 180^{\circ}
\widehat{xOz} + \widehat{zOt} = \widehat{yOt} = 180^{\circ}
Vậy \widehat{xOy} + \widehat{yOz} = \widehat{yOz}+ \widehat{zOt}
\Longrightarrow \widehat{xOy} = \widehat{zOt}
Chú ý: Ta có thể dùng dấu hiệu sau: 2 góc kề bù khi có chung đỉnh, chung một cạnh, 2 cạnh còn lại là 2 tia đối nhau.
Luyện tập vận dụng 4 trang 94
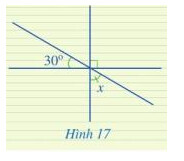
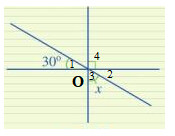
2 góc đối đỉnh thì bằng nhau
Ta có: \widehat{O_{2}} + \widehat{O_{3}}+\widehat{O_{4}}= 180^{\circ} (kề bù)
\Longrightarrow x + 30^{\circ} + 90^{\circ} = 180^{\circ}
\Longrightarrow x = 180^{\circ} – 30^{\circ} – 90^{\circ} = 60^{\circ}
Vậy x = 60^{\circ}
Giải bài tập SGK bài 1 chương 4
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Góc ở vị trí đặc biệt trang 9 SGK Toán 7 Cánh diều tập 1 dưới đây nhé!
Bài tập 1 trang 94
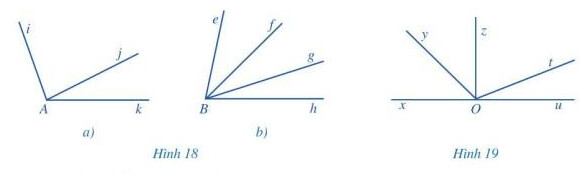
b) Tìm hai góc kề bù ở Hình 19.
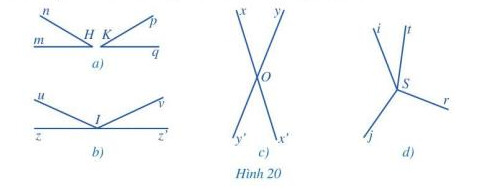
c) Tìm hai góc đối đỉnh trong mỗi hình 20a, 20b, 20c, 20d:
+ 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
+ 2 góc có tổng số đo là 180 độ là 2 góc bù nhau
+ 2 góc kề bù nếu chúng vừa kề nhau, vừa bù nhau
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
a) Hai góc kề nhau:
Trong hình 18a là: góc \widehat{iAj} và góc \widehat{jAk}
Trong hình 18b là: góc \widehat{eBf} và góc \widehat{fBg} ; góc \widehat{eBf} và góc \widehat{fBh} ; góc \widehat{eBg} và góc \widehat{gBh} ; góc \widehat{fBg} và góc \widehat{gBh}
b) 2 góc kề bù trong Hình 19 là: góc \widehat{xOy} và góc \widehat{yOu} ; góc \widehat{xOz} và góc \widehat{zOu} ; góc \widehat{xOt} và góc \widehat{tOu}
c) 2 góc đối đỉnh:
Trong Hình 20a: Không có vì 2 góc này không có chung đỉnh
Trong Hình 20b: Không có vì không có 2 góc nào mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Trong Hình 20c: góc xOy và góc x’Oy’
Trong Hình 20d: Không có vì không có 2 góc nào mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia
Bài 2 trang 95
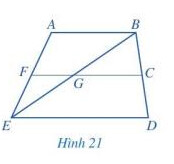
a) Hai góc kề nhau;
b) Hai góc kề bù (khác góc bẹt) ;
c) Hai góc đối đỉnh( khác góc bẹt và góc không).
+ 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
+ 2 góc có tổng số đo là 180 độ là 2 góc bù nhau
+ 2 góc kề bù nếu chúng vừa kề nhau, vừa bù nhau
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
a) 2 góc kề nhau là: góc \widehat{ABE} và \widehat{EBD} ; góc \widehat{AFG} và \widehat{GFE} ; góc \widehat{AEB} và \widehat{BED} ; góc \widehat{BCG} và \widehat{GCD} ; góc \widehat{FGB} và \widehat{BGC} ; góc \widehat{BGC} và \widehat{CGE} ; góc \widehat{CGE} và \widehat{EGF} ; góc \widehat{EGF} và \widehat{FGB} .
b) 2 góc kề bù là: góc \widehat{AFG} và \widehat{GFE} ; góc \widehat{BCG} và \widehat{GCD} ; góc \widehat{FGB} và \widehat{BGC} ; góc \widehat{BGC} và \widehat{CGE} ; góc \widehat{CGE} và \widehat{EGF} ; góc \widehat{EGF} và \widehat{FGB} .
c) 2 góc đối đỉnh là: góc \widehat{FGB} và \widehat{CGE} ; góc \widehat{BGC} và \widehat{EGF}
Bài 3 trang 95
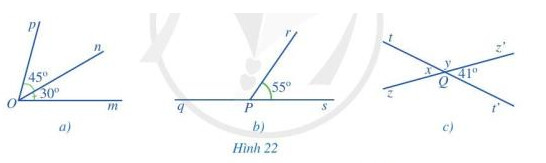
a) Góc mOp trong Hình 22a;
b) Góc qPr trong Hình 22b;
c) x,y trong Hình 22c.
+ Nếu tia On nằm trong góc mOp thì \widehat{mOn} + \widehat{nOp}= \widehat{mOp}
+ 2 góc kề bù có tổng số đo là 180 độ
+ 2 góc đối đỉnh thì bằng nhau
a) Vì tia On nằm trong góc mOp nên \widehat{mOn} + \widehat{nOp}= \widehat{mOp}
\Longrightarrow 30^{\circ} + 45^{\circ} = \widehat{mOp}
\Longrightarrow 75^{\circ} = \widehat{mOp}
Vậy số đo góc mOp là 75 độ
b) Ta có: \widehat{qPr} + \widehat{rPs} = 180^{\circ} (2 góc kề bù)
\Longrightarrow \widehat{qPr} + 55^{\circ} = 180^{\circ}
\Longrightarrow \widehat{qPr} = 180^{\circ} – 55^{\circ} = 125^{\circ}
Vậy số đo góc qPr là 125 độ
c) Ta có: \widehat{tQz} = \widehat{t’Qz’} (2 góc đối đỉnh), mà \widehat{t’Qz’} = 41^{\circ} \Longrightarrow \widehat{tQz} = 41^{\circ}
\widehat{tQz'} + \widehat{z'Qt} = 180^{\circ} ( 2 góc kề bù) nên \widehat{tQz'} + 41^{\circ} = 180^{\circ} \Longrightarrow \widehat{tQz'} + 41^{\circ} = 180^{\circ} \Longrightarrow \widehat{tQz'} = 180^{\circ} - 41^{\circ} = 139^{\circ}
Vậy {x} = 41^{\circ} ; {y} = 139^{\circ} ;
Bài 4 trang 95

+ Xác định số góc kề nhau được tạo bởi hai thanh chắn vòm cửa.
+ Góc bẹt có số đo là 180 độ.
Có 4 góc kề nhau và bằng nhau được tạo thành, xếp thành góc bẹt, mỗi góc tạo bởi 2 thanh chắn vòm cửa.
Do đó, mỗi góc có số đo: 180^{\circ} : 4 = 45^{\circ}
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Góc ở vị trí đặc biệt Chương 4 – 90, 91, 92, 93, 94, 95 Toán 7 Cánh diều tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt.





