Giải SGK bài 4 chương 7 trang 80, 81, 82, 83 Toán 7 Cánh Diều tập 2

Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động,hoạt động, luyện vận dụng, bài tập trong bài Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh ở các trang 80, 81, 82 SGK Toán 7 Cánh Diều tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.

Trả lời câu hỏi SGK trang 80, 81, 82 Toán 7 Cánh Diều

Khởi động bài học với những câu hỏi hoạt động và luyện tập vận dụng ở các trang 80, 81, 82 sẽ giúp bạn tiếp thu kiến thức về bài học “Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh” một cách dễ dàng hơn rất nhiều. Tham khảo ngay lời giải của HocThatGioi nhé!

Khởi động trang 80

Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có: $A B=A^{\prime} B^{\prime}, B C=B^{\prime} C^{\prime}, C A=C^{\prime} A^{\prime}$.

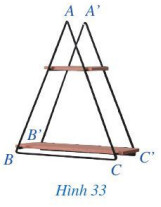
\text { Tam giác } A B C \text { có bằng tam giác } A^{\prime} B^{\prime} C^{\prime} \text { hay không? }

Phương pháp giải:
Quan sát Hình 33 để xem tam giác $A B C$ có bằng tam giác $A^{\prime} B^{\prime} C^{\prime}$ không.

Lời giải chi tiết:
Tam giác $A B C$ có bằng tam giác $A^{\prime} B^{\prime} C^{\prime}$ (vì 2 tam giác này có thể chồng khít lên nhau).

Hoạt động 1 trang 80

Cho hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ (Hình 34) có: $A B=A^{\prime} B^{\prime}=2 \mathrm{~cm}, A C=A^{\prime} C^{\prime}=3 \mathrm{~cm}$, $B C=B^{\prime} C^{\prime}=4 \mathrm{~cm}$. Hãy sử dụng thước đo góc để kiểm nghiệm rằng: $\widehat{A}=\widehat{A^{\prime}}, \widehat{B}=\widehat{B^{\prime}}$, $\widehat{C}=\widehat{C^{\prime}}$

Lời giải chi tiết:
\text { Hãy sử dụng thước đo góc để kiểm nghiệm rằng: } \widehat{A}=\widehat{A^{\prime}} ; \widehat{B}=\widehat{B^{\prime}} ; \widehat{C}=\widehat{C^{\prime}} \text {. }

Luyện tập vận dụng trang 81

Hai tam giác ở Hình 37 có bằng không? Vì sao?

Phương pháp giải:
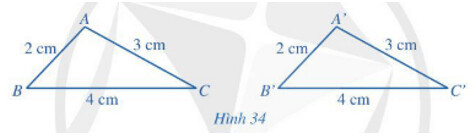
Hai tam giác bằng nhau nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia.

Lời giải chi tiết:
Xét tam giác $A B C$ và tam giác $A B D$ :
A C=A D ; B C=B D \text {; cạnh } A B \text { chung. }
Vậy $\triangle A B C=\Delta A B D$ (c.c.c)

Hoạt động 2 trang 82

Cho hai tam giác vuông $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có:
$\widehat{A}=\widehat{A^{\prime}}=90^{\circ}, A B=A^{\prime} B^{\prime}=3 \mathrm{~cm}, B C=B^{\prime} C^{\prime}=5 \mathrm{~cm}$ (Hình 39).
So sánh độ dài các cạnh $A C$ và $A^{\prime} C^{\prime}$.

Phương pháp giải:
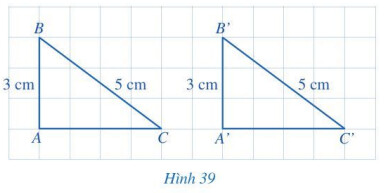
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Lời giải chi tiết:
Ta thấy $A C=4 \mathrm{~cm} ; A^{\prime} C^{\prime}=4 \mathrm{~cm}$.
Vậy $A C=A^{\prime} C^{\prime}$.

Giải bài tập SGK trang 83 Toán 7 Cánh Diều

Cùng xem cách HocThatGioi áp dụng các kiến thức đã được học ở trên về Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh để giải các bài tập cuối bài trong SGK Toán 7 Cánh Diều ở trang 83 như thế nào nhé!

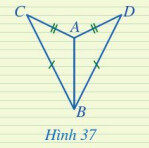
Bài 1 trang 83

1. Cho Hình 42 có $M N=Q N, M P=Q P$. Chứng minh $\widehat{M N P}=\widehat{Q N P}$.

Phương pháp giải:
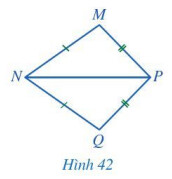
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Hai tam giác bằng nhau thì các cặp cạnh tương ứng và các cặp góc tương ứng bằng nhau.

Lời giải chi tiết:
Xét tam giác $M N P$ và tam giác $Q N P: M N=Q N ; M P=Q P$; NP chung.
Vậy $\Delta M N P=\Delta Q N P$ (с.с.с)
Vậy $\widehat{M N P}=\widehat{Q N P}$ ( 2 góc tương ứng)

Bài 2 trang 83

2. Cho Hình 43 có $A B=A D, \widehat{A B C}=\widehat{A D C}=90^{\circ}$. Chû́ng minh $\widehat{A C B}=\widehat{A C D}$.

Phương pháp giải:
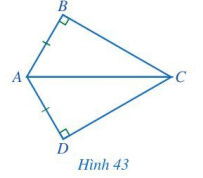
Nếu một cạnh góc vuông và một cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và một cạnh huyền của tam giác kia thì hai tam giác vuông đó bằng nhau.
Hai tam giác bằng nhau thì các cặp góc tương ứng bằng nhau.

Lời giải chi tiết:
Xét hai tam giác vuông $A B C$ và $A D C$ có: $A B=A D, A C$ chung.
Nên $\triangle A B C=\triangle A D C$ (cạnh huyền – cạnh góc vuông) nên $\widehat{A C B}=\widehat{A C D}$ (2 góc tương ứng)

Bài 3 trang 83

3. Cho Hình 44 có $A C=B D, \widehat{A B C}=\widehat{B A D}=90^{\circ}$. Chû́ng minh $A D=B C$.

Phương pháp giải:
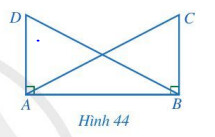
Nếu một cạnh góc vuông và một cạnh huyền của tam giác vuông này bằng một cạnh góc vuông và một cạnh huyền của tam giác kia thì hai tam giác vuông đó bằng nhau.
Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.

Lời giải chi tiết:
Xét hai tam giác vuông có:
$D A B$ và $C B A: A C=B D ; A B$ chung.
Nên $\triangle D A B=\triangle C B A$ (cạnh huyền – cạnh góc vuông)
Nên $A D=B C$ ( 2 cạnh tương ứng)

Bài 4 trang 83

4. Cho hai tam giác $A B C$ và $M N P$ thoả mãn: $A B=M N, B C=N P, A C=M P, \widehat{A}=65^{\circ}$, $\widehat{N}=71^{\circ}$. Tính số đo các góc còn lại của hai tam giác.

Phương pháp giải:
Hai tam giác bằng nhau thì các cặp góc tương ứng bằng nhau. Và tổng ba góc trong một tam giác bằng 180°.

Lời giải chi tiết:

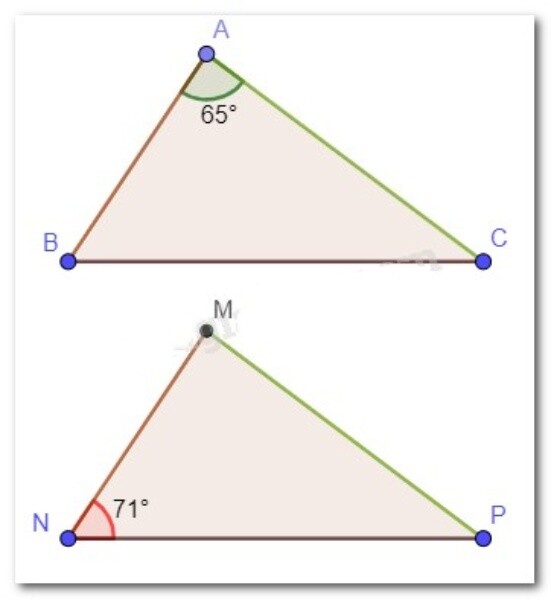
Tam giác $A B C$ và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau:
$A B=M N, B C=N P, A C=M P)$.
Nên các cặp góc tương ứng trong hai tam giác này bằng nhau:
$\widehat{A}=\widehat{M}, \widehat{B}=\widehat{N}, \widehat{C}=\widehat{P}$
Vậy $\widehat{A}=\widehat{M}=65^{\circ} ; \widehat{B}=\widehat{N}=71^{\circ}$;
$\widehat{C}=\widehat{P}=180^{\circ}-65^{\circ}-71^{\circ}=44^{\circ}$ (vì tổng ba góc trong một tam giác bằng $180^{\circ}$ ).

Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 4 chương 7 – Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh trang 80, 81, 82, 83 Toán 7 Cánh Diều tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!

Bài viết khác liên quan đến Lớp 7 – Toán – 2 tam giác bằng nhau ccc

• Giải SGK bài 13 trang 63,67 Toán 7 Kết nối tri thức tập 1