Giải SGK Bài 5 Chương 6 trang 64, 65, 66, 67 Toán 7 Cánh diều tập 2
Ở bài viết lần này, HocThatGioi sẽ trả lời các câu hỏi và bài tập trong bài Phép chia đa thức một biến. Đây là bài học thuộc bài 5 chương VI trang 64, 65, 66, 67 SGK Toán 7 Cánh diều tập 2. Hy vọng những lời giải chi tiết dưới đây sẽ giúp bạn hiểu và nắm rõ các kiến thức của bài học này.
Trả lời câu hỏi SGK Bài 5 Chương 6 Toán 7 Cánh diều tập 2
Mở đầu bài học bằng những câu hỏi khởi động và phần luyện tập vận dụng của bài Phép chia đa thức một biến dưới đây sẽ giúp bạn dễ dàng tiếp thu kiến thức về bài học.
Câu hỏi khởi động trang 64
$(x^3+1):(x^2-x+1)$
Làm thế nào để thực hiện được phép chia một đa thức cho một đa thức khác?
Đọc kĩ phần III. Chia đa thức một biến đã sắp xếp.
Để thực hiện phép chia một đa thức cho một đa thức khác, ta làm như sau:
Bước 1:
Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
– Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
– Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.
Hoạt động 1 trang 64
a) $x^5: x^3$
b) $(4 x^3): x^2$
c) $(a x^m):(b x^n)(a \neq 0 ; b \neq 0 ; m, n \in N, m \geq n)$.
Muốn thực hiện những phép chia trên, ta lấy hệ số của đơn thức bị chia chia cho hệ số của đơn thức chia và lấy biến của đơn thức bị chia chia cho biến của đơn thức chia. Rồi nhân 2 kết quả đó với nhau.
$x^m: x^n=x^{m-n}(m, n \in N, m \geq n)$
a) $x^5: x^3=x^{5-3}=x^2$,
b) $(4 x^3): x^2=(4: 1) .(x^3: x^2)=4 x$;
c) $(a x^m):(b x^n)=(a: b) .(x^m: x^n)=(a: b) . x^{m-n}(a \neq 0 ; b \neq 0 ; m, n \in N, m \geq n)$.
Hoạt động 2 trang 64
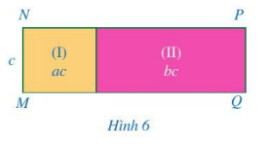
a) Tính NP
b) So sánh: $(A+B): c$ và $A: c+B: c$
a) $N P$ là độ dài của một cạnh hình chữ nhật. Để tính được $N P$ ta phải tính được diện tích của hình chứa $N P$. Hoặc tính độ dài của hai cạnh hợp thành $N P$ với diện tích của hình (I), (II) đã cho.
b) Thực hiện hai phép chia $(A+B): c$ và $A: c+B:c$ rồi so sánh kết quả.
a) Ta có: Diện tích hình chữ nhật $M N P Q$ bằng diện tích hình chữ nhật (I) + diện tích hình chữ nhật (II)
$=a c+b c=(a+b) . c$
Mà $M N=c$
Do đó $N P=(a+b) . c: c=a+b$
b) Ta có:
$(A+B): c=(a c+b c): c=a+b$
$A: c+B: c=a c: c+b c: c=a+b$
Vậy $(A+B): c=A: c+B: c$.
Luyện tập vận dụng 1 trang 64
a) $(3 x^6):(0,5 x^4)$
b) $(-12 x^{m+2}):(4 x^{n+2})(m, n \in N, m \geq n)$
Muốn chia đơn thức $A$ cho đơn thức $B(B \neq 0)$ khi số mũ của biến trong $A$ lớn hơn hoặc bằng số mũ của biến đó trong $B$, ta làm như sau:
– Chia hệ số của đơn thức $A$ cho hệ số của đơn thức $B$;
– Chia lũy thừa của biến trong $A$ cho lũy thừa của biến đó trong $B$;
– Nhân các kết quả vừa tìm được với nhau.
a) $(3 x^6):(0,5 x^4)=(3: 0,5) .(x^6: x^4)=6 . x^{6-4}=6 x^2$
b) $(-12 x^{m+2}):(4 x^{n+2})=(-12: 4).(x^{m+2}: x^{n+2})=-3 . x^{m+2-n-2}=-3 . x^{m-n}(m, n \in N, m \geq n)$
Luyện tập vận dụng 2 trang 65
$(\frac{1}{2} x^4-\frac{1}{4} x^3+x):(-\frac{1}{8} x)$
Muốn chia đa thức $P$ cho đơn thức $Q(Q \neq 0)$ khi số mũ của biến ở mỗi đơn thức của $P$ lớn hơn hoặc bằng số mũ của biến đó trong $Q$, ta chia mỗi đơn thức của $P$ cho đơn thức $Q$ rồi cộng các thương với nhau.
$(\frac{1}{2} x^4-\frac{1}{4} x^3+x):(-\frac{1}{8} x)$
$=\frac{1}{2} x^4:(-\frac{1}{8} x)-\frac{1}{4} x^3:(-\frac{1}{8} x)+x:(-\frac{1}{8} x)$
$=(\frac{1}{2}:-\frac{1}{8}) .(x^4: x)-(\frac{1}{4}:-\frac{1}{8}) .(x^3: x)+(1:-\frac{1}{8}) .(x: x)$
$=-4 . x^{4-1}-(-2). x^{3-1}+(-8) . x^{1-1}$
$=-4 x^3+2 x^2-8$
Luyện tập vận dụng 3 trang 66
a) $(x^3+1):(x^2-x+1)$;
b) $(8 x^3-6 x^2+5):(x^2-x+1)$.
Để chia một đa thức cho một đa thức khác không (hai đa thức đều đã thu gọn và sắp xếp theo số mũ giảm dần), ta làm như sau:
Bước 1:
– Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
– Nhân kết quả trên với đa thức chia và đặt dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
– Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.
a)
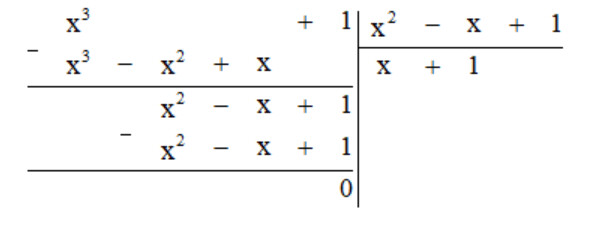
Vậy $(x^3+1):(x^2-x+1)=x+1$
b)
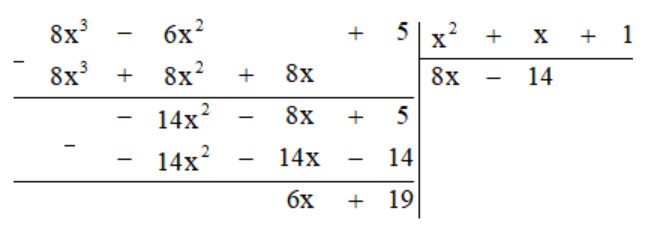
Vậy $(8x^3-6x^2+5)=(x^2-x+1)(8x+2)+(-6x+3)$
Giải bài tập SGK Bài 5 Chương 6 Toán 7 Cánh diều tập 2
Sau khi đã tìm hiểu phần nội dung của bài học, cùng ôn lại những kiến thức đã học qua phần giải đáp chi tiết các bài tập trong SGK Toán 7 Cánh diều tập 2 trang 67 dưới đây nhé.
Bài tập 1 trang 67
a) $(4 x^3):(-2 x^2)$
b) $(-7 x^2):(6 x)$
c) $(-14 x^4):(-8 x^3)$
Muốn chia đơn thức $A$ cho đơn thức $B(B \neq 0)$ khi số mũ của biến trong $A$ lớn hơn hoặc bằng số mũ của biến đó trong $B$, ta làm như sau:
Chia hệ số của đơn thức $A$ cho hệ số của đơn thức $B$;
– Chia lũy thừa của biến trong $A$ cho lũy thừa của biến đó trong $B$;
– Nhân các kết quả vừa tìm được với nhau.
a)$(4 x^3):(-2 x^2)$
$=[4:(-2)] .(x^3: x^2)$
$=-2 . x^{3-2}=-2 x$
b)$(-7 x^2):(6 x)$
$=(-7: 6).(x^2: x)$
$=-\frac{7}{6}. x^{2-1}=-\frac{7}{6}.x$
c)$(-14 x^4):(-8 x^3)$
$=(-14:-8) .(x^4: x^3) $
$=\frac{7}{4}. x^{4-3}=\frac{7}{4}. x$
Bài tập 2 trang 67
a) $(8 x^3+2 x^2-6 x):(4 x)$
b) $(5 x^3-4 x):(-2 x)$
c) $(-15 x^6-24 x^3):(-3 x^2)$
Muốn chia đa thức $\mathrm{P}$ cho đơn thức $\mathrm{Q}(\mathrm{Q} \neq 0)$ khi số mũ của biến ở mỗi đơn thức của $\mathrm{P}$ lớn hơn hoặc bằng số mũ của biến đó trong $\mathrm{Q}$, ta chia mỗi đơn thức của $\mathrm{P}$ cho đơn thức $\mathrm{Q}$ rồi cộng các thương với nhau.
a) $(8 x^3+2 x^2-6 x):(4 x)=8 x^3:(4 x)+2 x^2:(4 x)-(6 x):(4 x)$
$=(8: 4) .(x^3: x)+(2: 4).(x^2: x)-(6: 4) .(x: x)$
$=2 x^2+\frac{1}{2} x-\frac{3}{2}$
b) $(5 x^3-4 x):(-2 x)=5 x^3:(-2 x)-4 x:(-2 x)$
$=(5:-2) .(x^3: x)-(4:-2) .(x: x)$
$=-\frac{5}{2} x^{3-1}-(-2)=-\frac{5}{2} x^2+2$
c) $(-15 x^6-24 x^3):(-3 x^2)=(-15 x^6):(-3 x^2)+(-24 x^3):(-3 x^2)$
$=(-15:-3) .(x^6: x^2)+(-24:-3).(x^3: x^2)$
$=5 . x^{6-2}+8 .x^{3-2}=5 x^4+8 x$
Bài tập 3 trang 67
a) $(x^2-2 x+1):(x-1)$
b) $(x^3+2 x^2+x):(x^2+x)$
c) $(-16 x^4+1):(-4 x^2+1)$
d) $(-32 x^5+1):(-2 x+1)$
Để chia một đa thức cho một đa thức khác không (hai đa thức đều đã thu gọn và sắp xếp theo số mũ giảm dần), ta làm như sau:
Bước 1:
– Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
– Nhân kết quả trên với đa thức chia và đặt dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
– Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.
a) Thực hiện phép tính ta được:
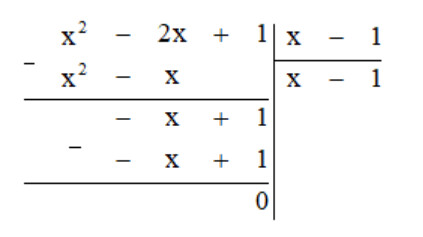
Vậy $(x^2 – 2x + 1) : (x – 1) = x – 1$
b) Thực hiện phép tính ta được:
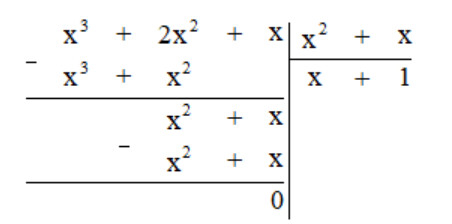
Vậy $(x^3 + 2x^2 + x) : (x^2 + x) = x + 1$
c) Thực hiện phép tính ta được:
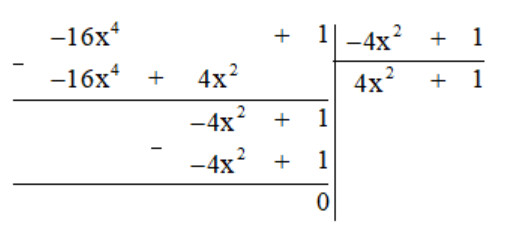
Vậy $(-16x^4 + 1) : (-4x^2 + 1) = 4x^2 + 1$
d) Thực hiện phép tính ta được:
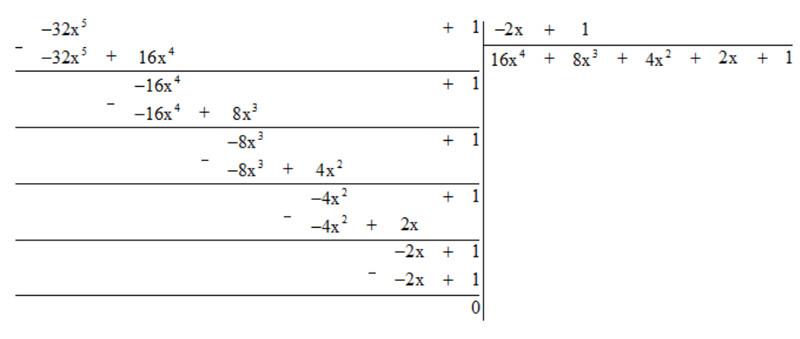
Vậy $(-32 x^5+1):(-2 x+1)=16 x^4+8 x^3+4 x^2+2 x+1$
Bài tập 4 trang 67
a) $(6 x^2-2 x+1):(3 x-1)$
b) $(27 x^3+x^2-x+1):(-2 x+1)$
c) $(8 x^3+2 x^2+x):(2 x^3+x+1)$
d) $(3 x^4+8 x^3-2 x^2+x+1):(3 x+1)$
Để chia một đa thức cho một đa thức khác không (hai đa thức đều đã thu gọn và sắp xếp theo số mũ giảm dần), ta làm như sau:
Bước 1:
– Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
– Nhân kết quả trên với đa thức chia và đặt dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
– Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.
a) Thực hiện phép tính ta được:
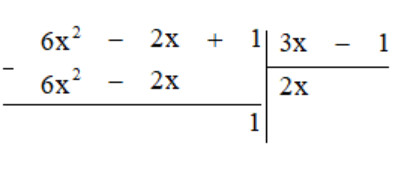
Vậy $(6 x^2-2 x+1)=(3 x-1) .(2 x)+1$
b) Thực hiện phép tính ta được:
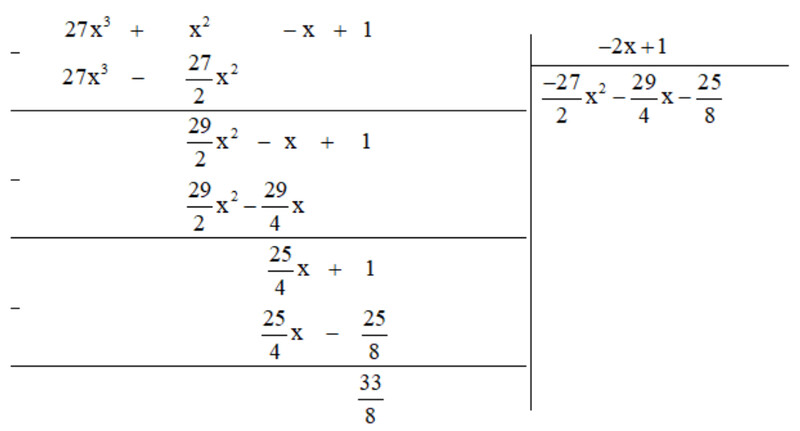
Vậy $27 x^3+x^2-x+1=(\frac{-27}{2} x^2-\frac{29}{4} x-\frac{25}{8}).(-2 x+1)+\frac{33}{8}$
c) Thực hiện phép tính ta được:
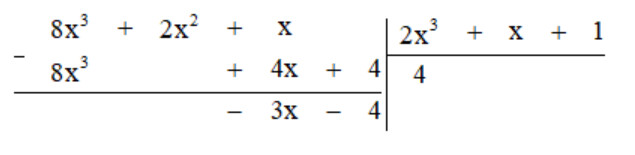
Vậy $8x^3 + 2x^2 + x = 4(2x^3 + x + 1) + (-3x – 4)$.
d) Thực hiện phép tính ta được:
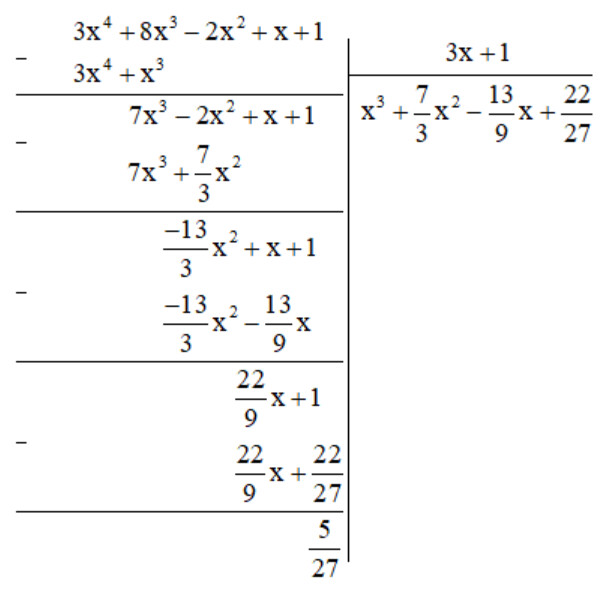
Bài tập 5 trang 67
Số sản phẩm mà công ty đó bán được bằng doanh thu chia cho giá của mỗi sản phẩm (sau khi tăng).
Giá tiền mỗi sản phẩm sau khi tăng giá là $2 x+30$ (nghìn đồng).
Sau khi tăng giá thì công ty có doanh thu là $6 x^2+170 x+1200$ (nghìn đồng). Vậy số sản phẩm mà công ty đó đã bán được theo $x$ là:
$(6 x^2+170 x+1200):(2 x+30)=3 x+40$ (sản phẩm)
Bài tập 6 trang 67
Thể tích hình hộp chữ nhật bằng diện tích đáy nhân chiều cao.
Để tính chiều chiều cao của hình hộp chữ nhật, ta lấy thể tích hình hộp chữ nhật chia cho diện tích đáy. (Trong bài trên, diện tích đáy của hình hộp chữ nhật là hình chữ nhật và bằng chiều dài nhân chiều rộng hay bằng tích của 2 cạnh).
Diện tích mặt đáy của hình hộp chữ nhật là:
$(x+1) .(x+2)=x(x+2)+1.(x+2)$
$=x^2+2 x+x+2=x^2+3 x+2$ $(c m^2)$
Vậy chiều cao của hình hộp chữ nhật đó theo $x$ là:
$(x^3+6 x^2+11 x+6):(x^2+3 x+2)=x+3(\mathrm{~cm})$
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Bài 5 Chương VI Biểu thức đại số trang 64, 65, 66, 67 sách Toán 7 Cánh diều tập 2. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn học tốt!





