Giải SGK bài 5 chương 7 trang 84, 85, 86, 87 Toán 7 Cánh Diều tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, hoạt động, vận dụng – luyện tập và bài tập trong bài Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh. Các bài tập sau đây thuộc bài 5 chương 7 ở các trang 84, 85, 86, 87. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK trang 84, 85 Toán 7 Cánh diều tập 2
Những lời giải dưới đây sẽ giúp bạn đi tìm đáp án cho các hoạt động khởi động, luyện tập và vận dụng ở các trang 84, 85 Toán 7 Cánh diều trong bài Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh một cách nhanh chóng và dễ hiểu. Cùng theo dõi ngay nhé!
Khởi động trang 84
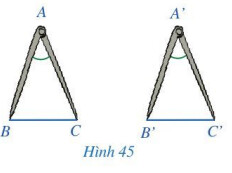
\text { Hai tam giác } A B C \text { và } A^{\prime} B^{\prime} C^{\prime} \text { có bằng nhau hay không? }
Học sinh có thể dùng thước để đo độ dài cạnh $B C$ và $B^{\prime} C^{\prime}$ rồi so sánh.
\text { Hai tam giác } A B C \text { và } A^{\prime} B^{\prime} C^{\prime} \text { có bằng nhau. }
Hoạt động 1 trang 84
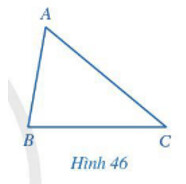
Hai cạnh của góc tại đỉnh A là cạnh AB và cạnh AC.
Hoạt động 2 trang 84
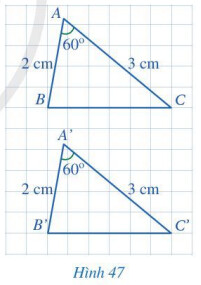
Đếm số ô vuông rồi so sánh $B C$ và $B^{\prime} C^{\prime}$. Từ đó so sánh hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$
$B C=B^{\prime} C^{\prime}=6$ (ô vuông).
Tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có các cặp cạnh tương ứng bằng nhau nên tam giác $A B C$ bằng tam giác $A^{\prime} B^{\prime} C$ (c.c.c)
Luyện tập vận dụng 1 trang 85
Chứng minh tam giác $O M Q$ bằng tam giác $O P N$. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau.
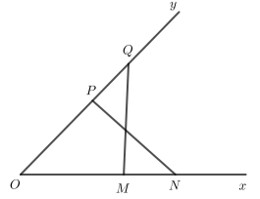
Xét tam giác $O M Q$ và tam giác $O P N$ có:
$O M=O P(=2 \mathrm{~cm}) ; O Q=O N$ (= $3 \mathrm{~cm})$; góc $O$ chung.
Vậy $\triangle O M Q=\triangle O P N$ (c.g.c)
$\Rightarrow M Q=N P$ ( 2 cạnh tương ứng)
Luyện tập vận dụng 2 trang 85
Muốn chứng minh $M P=N P$, ta chứng minh tam giác $M O P$ bằng tam giác NOP.
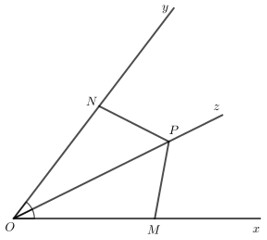
Do $\mathrm{Oz}$ là tia phân giác của góc $x \mathrm{Oy}$ nên $\widehat{x O z}=\widehat{y \mathrm{O} z}$.
Xét $\triangle \mathrm{MOP}$ và $\triangle \mathrm{NOP}$ có:
$\mathrm{OM}=\mathrm{ON}$ (theo giả thiết).
$\widehat{M O P}=\widehat{N O P}$ (chứng minh trên).
OP chung.
Suy ra $\triangle \mathrm{MOP}=\triangle \operatorname{NOP}(\mathrm{c}-\mathrm{g}-\mathrm{c})$.
Do đó MP = NP ( 2 cạnh tương ứng).
Giải bài tập SGK trang 86, 87 Toán 7 Cánh diều tập 2
Cùng xem cách HocThatGioi áp dụng các kiến thức về Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh ở trên để giải các bài tập cuối bài trong SGK ở trang 86, 87 Toán 7 Cánh diều như thế nào nhé!
Bài 1 trang 86
Cho tam giác $A B C$ có $A B \lt A C$. Tia phân giác của góc $B A C$ cắt cạnh $B C$ tại điểm $D$. Điểm $E$ thuộc cạnh $A C$ thoả mãn $A E=A B$. Chứng minh:
a) $\triangle A B D=\triangle A E D$
b) $\widehat{B}>\widehat{C}$.
a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c.
b) Chứng minh $\widehat{B}>\widehat{C}$ dựa vào kết quả phần a và tổng ba góc trong một tam giác bằng $180^{\circ}$.
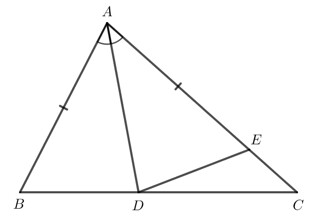
a) Do AD là tia phân giác của $\widehat{B A C}$ nên $\widehat{B A \mathrm{D}}=\widehat{C A \mathrm{D}}$.
Xét $\triangle A B D$ và $\triangle A E D$ có:
$A B=A E$ (theo giả thiết).
$\widehat{D A B}=\widehat{D A E}$ (chứng minh trên).
AD chung.
Suy ra $\triangle \mathrm{ABD}=\triangle \mathrm{AED}(\mathrm{c}-\mathrm{g}-\mathrm{c})$
b) \text { Do } \triangle \mathrm{ABD}=\triangle \mathrm{AED}(\mathrm{c}-\mathrm{g}-\mathrm{c} \text { ) nên } \widehat{A B \mathrm{D}}=\widehat{A E D} \text { (2 góc tương ứng). }
Ta có $\widehat{A E D}$ là góc ngoài tại đỉnh $E$ của $\triangle \mathrm{ECD}$ nên $\widehat{A \mathrm{ED}}=\widehat{E C \mathrm{D}}+\widehat{E \mathrm{EC}}>\widehat{E C \mathrm{D}}$
Hay $\widehat{A B \mathrm{D}}>\widehat{E C \mathrm{D}}$
Do đó $\widehat{B}>\widehat{C}$.
Bài 2 trang 86
a) $I A=I B$;
b) $/H$ là tia phân giác của góc $A I B$.
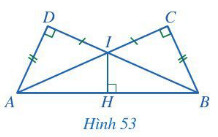
a) Chứng minh $I A=I B$, ta chứng minh tam giác $I D A$ bằng tam giác $I C B$.
b) Một đường thẳng là đường vuông góc hạ từ một đỉnh của tam giác cân tại đỉnh đó thì đường thẳng đó là tia phân giác của tam giác đó.
a) Xét tam giác $I D A$ và tam giác $I C B$ có:
I D=I C(g t), D A=C B(g t), \widehat{D}=\widehat{C}=90^{\circ} \text {. }
Vậy $\Delta I D A=\Delta I C B$ (c.g.c)
$\Rightarrow I A=I B$ (2 cạnh tương ứng)
b) Xét tam giác vuông IHA và tam giác vuông IHB có:
$\mathrm{IH}$ chung; $I A=I B(g t)$
Vậy $\Delta I H A=\Delta I H B$ (cạnh huyền – cạnh góc vuông)
$\Rightarrow \widehat{A I H}=\widehat{B I H}$ ( 2 góc tương ứng)
Mà tia IH nằm trong góc $\mathrm{AIB}$
$\Rightarrow I H$ là tia phân giác của góc $A I B$.
Bài 3 trang 86
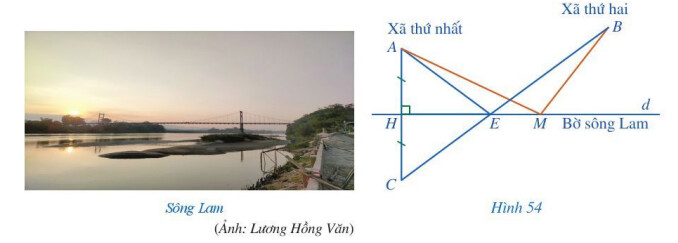
– Kí hiệu điểm $A$ chỉ vị trí xã thứ nhất, điểm $B$ chỉ vị trí xã thứ hai, đường thẳng $d$ chỉ vị trí bờ sông Lam.
– Kẻ $A H$ vuông góc với $d(H$ thuộc $d)$, kéo dài $A H$ về phía $H$ và lấy điểm $C$ sao cho $A H=H C$.
– Nối $C$ với $B, C B$ cắt đường thẳng $d$ tại điểm $E$.
Khi đó, $E$ là vị trí của cây cầu.
Bạn Nam nói rằng: Lấy một điểm $M$ trên đường thẳng $d, M$ khác $E$ thì M A+M B \gt E A+E B .
Em hãy cho biết bạn Nam nói đúng hay sai. Vì sao?
Muốn biết bạn Nam nói đúng hay không, ta chứng minh bất đẳng thức $M A+M B \gt E A+E B$ là đúng hay sai.
Dựa vào:
– Tính chất đường trung trực.
– Trong một tam giác, tổng của hai cạnh luôn lớn hơn độ dài cạnh còn lại.
Ta có: $H A=H C, E H \perp A C$. Vậy $E H$ là đường trung trực của $\mathrm{AC}$ nên $E A=E C$ (tính chất đường trung trực của đoạn thẳng).
Tương tự ta có: $M H$ là đường trung trực của $\mathrm{AC}$ nên $M A=$ $M C$.
Xét tam giác $M B C: B C\lt M B+M C$ (Trong một tam giác, tổng của hai cạnh luôn lớn hơn độ dài cạnh còn lại).
Ta có:
B C \lt M B+M C=M B+M A \text { (1) }
$\mathrm{Ba}$ điểm $B, E, C$ thẳng hàng nên $E B+E C=B C$. (2)
Thay (2) vào (1) ta được:
B C\lt M B+M A \\ E B+E C\lt M A+M B
Mà $E A=E C$ nên $E A+E B\lt M A+M B$. Vậy bạn Nam nói đúng và khi đó để tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất thì $E$ là vị trí của cây cầu.
Bài 4 trang 87
a) $A D=M Q$;
b) $D E=Q R$.
a) Chứng minh tam giác $A B D$ bằng tam giác $M N Q$.
b) Chứng minh tam giác $D E C$ bằng tam giác $Q R P$.
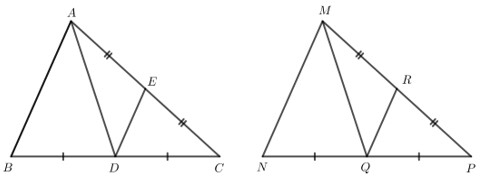
a) Xét hai tam giác $A B D$ và tam giác $M N Q$ :
A B=M Q(\text { do } \Delta A B C=\Delta M N P) \\ \widehat{A B D}=\widehat{M N Q}(\widehat{A B D}=\widehat{M N Q}) \\ B D=N Q\left(\frac{1}{2} B C=\frac{1}{2} N P\right) \\ B C=N P(\text { do } \Delta A B C=\Delta M N P)
Vậy $\triangle A B D=\Delta M N Q$ (c.g.c) nên $A D=M Q$ ( 2 cạnh tương ứng)
b) Vì $\Delta A B C=\Delta M N P$ nên $B C=N P$ ( 2 cạnh tương ứng). Do đó, $\frac{1}{2} B C=\frac{1}{2} N P$ hay $D C=Q P$
Vì $\triangle A B C=\triangle M N P$ nên $A C=M P$ ( 2 cạnh tương ứng)
Do đó, $\frac{1}{2} A C=\frac{1}{2} M P$ hay $E C=R P$
Xét hai tam giác $D E C$ và tam giác $Q R P$ :
$D C=Q P$
$\widehat{E C D}=\widehat{R P Q}(\Delta A B C=\Delta M N P)$
$E C=R P$
Vậy $\triangle D E C=\Delta Q R P$ (c.g.c) nên $D E=Q R$ ( 2 cạnh tương ứng)
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài 5 – Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh, thuộc chương 7 trang 84, 85, 86, 87 Toán 7 Cánh Diều tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





