Giải SGK bài Tam giác cân trang 93, 94, 95, 96 Toán 7 Cánh Diều tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Tam giác cân. Đây là bài học thuộc bài 7 chương 7 SGK Toán 7 Cánh Diều trang 93, 94, 95, 96. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi SGK trang 93, 94, 95 Toán 7 Cánh Diều
Các hoạt động khám phá, thực hành, vận dụng luyện tập ở các trang 93, 94, 95 này sẽ giúp các bạn đi vào bài học tìm hiểu các kiến thức về Tam giác cân một cách trơn tru và dễ hiểu hơn rất nhiều đấy! Cùng xem lời giải của HocThatGioi nhé!
Khởi động trang 93

Tam giác ABC như vậy gọi là tam giác gì?
Tam giác ABC là tam giác cân.
Hoạt động 1 trang 93
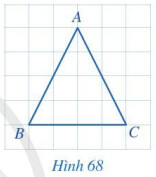
Quan sát Hình 68 , đo độ dài cạnh AB và AC rồi so sánh.
Hai cạnh AB và AC của tam giác ABC có bằng nhau.
Hoạt động 2 trang 94
a) Hai tam giác $A B D$ và $A C D$ có bằng nhau hay không? Vi sao?
b) Hai góc $B$ và $C$ có bằng nhau hay không? Vi sao?
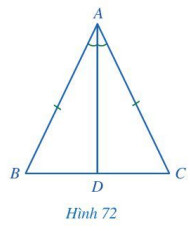
a) So sánh hai tam giác $A B D$ và tam giác $A C D$ theo trường hợp c.g.c.
b) Sử dụng kết quả phần a) để xét hai góc $B$ và góc $C$. Hai tam giác bằng nhau thì các cặp góc tương ứng bằng nhau.
a) Xét hai tam giác $A B D$ và $A C D$ có:
$A B=A C$
$\widehat{B A D}=\widehat{C A D}(A D$ là phân giác của góc $A)$
$A D$ chung
Vậy $\Delta A B D=\Delta A C D$ (c.g.c)
b) $\Delta A B D=\Delta A C D$ nên $\widehat{B}=\widehat{C}$ ( 2 góc tương ứng)
Hoạt động 3 trang 94
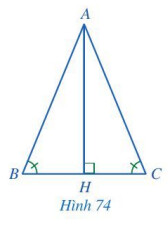
a) Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao?
b) Hai cạnh AB và AC có bằng nhau hay không? Vì sao?
a) Xét hai tam giác $B A H$ và $C A H$ theo trường hợp g.c.g.
b) Sử dụng kết quả phần a) để xét hai cạnh $A B$ và $A C$. Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau
a) $\widehat{B}=\widehat{C}$. Mà tổng ba góc trong một tam giác bằng $180^{\circ}$ nên $\widehat{B A H}=\widehat{C A H}$
Xét hai tam giác $\mathrm{BAH}$ và $\mathrm{CAH}$ có:
\widehat{B A H}=\widehat{C A H}
AH chung;
\widehat{A H B}=\widehat{A H C}\left(=90^{\circ}\right) \text {. }
Vậy $\Delta B A H=\Delta C A H$ (g.c.g)
b) $\triangle B A H=\triangle C A H$ nên $A B=A C$ ( 2 cạnh tương ứng).
Luyện tập vận dụng trang 95
Chứng minh tam giác $A M N$ cân bằng cách chứng minh hai góc $A M N$ và $A N M$ bằng nhau.
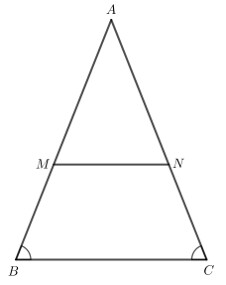
Tam giác $A B C$ cân tại A nên $\widehat{A B C}=\widehat{A C B}$.
Do MN // BC nên $\widehat{A M N}=\widehat{A B C}$ (2 góc đồng vị) và $\widehat{A N M}=\widehat{A C B}$ (2 góc đồng vị).
Mà $\widehat{A B C}=\widehat{A C B}$ nên $\widehat{A M N}=\widehat{A N M}$.
Tam giác $A M N$ có $\widehat{A M N}=\widehat{A N M}$ nên tam giác AMN cân tại $\mathrm{A}$.
Vậy tam giác AMN cân tại $A$.
Giải bài tập SGK trang 96
Những bài tập SGK ở cuối bài Tam giác cân trang 96 sách Toán 7 Cánh Diều sẽ giúp các bạn vận dụng những kiến thức vừa học để giải các bài tập từ cơ bản đến nâng cao. Cùng HocThatGioi giải quyết những bài toán này nhé!
Bài 1 trang 96
Chứng minh $B M=C N$ bằng cách chứng minh tam giác $A M B$ bằng tam giác $A N C$.
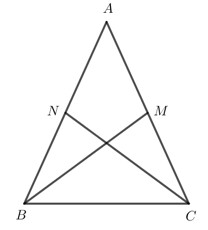
Tam giác $A B C$ cân nên $A B=A C$.
$M$ và $N$ lần lượt là trung điểm của $A C$ và $A B$ nên:
A N=B N=\frac{1}{2} A B \\ A M=C M=\frac{1}{2} A C
Mà $A B=A C$ nên $A N=B N=A M=C M$.
Xét tam giác $A M B$ và tam giác $A N C$ có:
$\widehat{A}$ chung;
A B=A C \\ A M=A N
Vậy $\Delta A M B=\Delta A N C$ (c.g.c) nên $B M=C N$ ( 2 cạnh tương ứng).
Bài 2 trang 96
Chứng minh tam giác $A D E$ đều ta chứng minh ba góc trong tam giác $A D E$ đều bằng $60^{\circ}$.
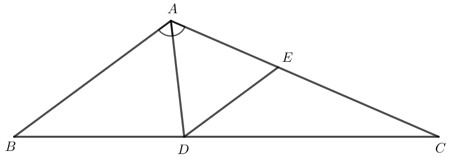
Do AD là tia phân giác của $\widehat{B A C}$ nên $\widehat{D A B}=\widehat{D A E}=\frac{1}{2} \widehat{B A C}=60^{\circ}$.
Do $D E / / A B$ nên $\widehat{D A B}=\widehat{A D E}$ (2 góc so le trong).
Do đó $\widehat{A \mathrm{D} E}=60^{\circ}$.
Xét $\triangle \mathrm{ADE}$ có: $\widehat{A E \mathrm{D}}=180^{\circ}-\widehat{D A \mathrm{E}}-\widehat{A \mathrm{DE}}=180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}$.
Tam giác $\mathrm{ADE}$ có $\widehat{D A \mathrm{E}}=\widehat{A \mathrm{DE}}=\widehat{A \mathrm{ED}}=60^{\circ}$ nên tam giác $\mathrm{ADE}$ đều.
Bài 3 trang 96
Ta chứng minh tam giác $M A B$ vuông cân bằng cách chứng minh trong tam giác có một góc vuông tại một đỉnh và có cặp cạnh bằng nhau xuất phát từ đỉnh đó.
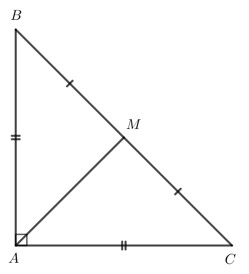
Tam giác $A B C$ vuông cân tại $A$ nên
\widehat{A}=90^{\circ} ; \widehat{B}=\widehat{C} ; A B=A C \text {. }
Tổng ba góc trong một tam giác bằng $180^{\circ}$ nên $\widehat{B}=\widehat{C}=90: 2=45^{\circ}$
Xét tam giác $A B M$ và tam giác ACM có:
$A B=A C$
AM chung
\mathrm{BM}=\mathrm{CM} \\ \Rightarrow \Delta A B M=\Delta A C M \text { (c.c.c) } \\ \Rightarrow \widehat{B A M}=\widehat{C A M} \text { (2 góc tương ứng) } \\ \text { Mà } \widehat{B A M}+\widehat{C A M}=\widehat{B A C}=90^0 \\ \Rightarrow \widehat{B A M}=\widehat{C A M}=90: 2=45^{\circ}
Xét tam giác $M A B$ :
\widehat{M B A}=\widehat{B A M}=45^{\circ} \Rightarrow \widehat{B M A}=90^{\circ} ; M B=M A \text {. }
Vậy tam giác $M A B$ vuông cân tại $M$.
Bài 4 trang 96
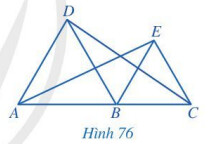
a) $A D / / B E$ và $B D / / C E$;
b) $\widehat{A B E}=\widehat{D B C}=120^{\circ}$;
c) $A E=C D$.
a) Ta chứng minh $A D / / B E$ và $B D / / C E$ dựa vào các cặp góc bằng nhau ở vị trí đồng vị.
b) Chứng minh $\widehat{A B E}=\widehat{D B C}=120^{\circ}$ dựa vào số đo góc của ba điểm thẳng hàng là $180^{\circ}$.
c) Chứng minh $A E=C D$ bằng cách chứng minh tam giác $A B E$ bằng tam giác $D B C$
a)
Tam giác $A B D$ và $B C E$ là tam giác đều nên
$\widehat{E B C}=\widehat{D A B}=60^{\circ}$ và $A, B, C$ thẳng hàng. Hai góc $E B C$ và $D A B$ ở vị trí đồng vị nên $A D / / B E$.
Tam giác $A B D$ và $B C E$ là tam giác đều nên
$\widehat{D B A}=\widehat{E C B}=60^{\circ}$ và $A, B, C$ thẳng hàng. Hai góc $D B A$ và $E C B$ ở vị trí đồng vị nên $B D / / C E$.
b)
Ta có $A, B, C$ thẳng hàng nên góc $A B C$ bằng $180^{\circ}$. Mà $\widehat{D B A}=\widehat{E B C}=60^{\circ} \Rightarrow \widehat{D B E}=60^{\circ}$.
Vậy $\widehat{A B E}=\widehat{D B C}=120^{\circ}($
$\widehat{A B E}=\widehat{D B A}+\widehat{D B E} ; \widehat{D B C}=\widehat{D B E}+\widehat{E B C})$.
c) Tam giác $A B D$ và $B C E$ là tam giác đều
\Rightarrow A B=A D, B E=B C
Xét hai tam giác $A B E$ và $D B C$ có:
A B=D B \\ \widehat{A B E}=\widehat{D B C}=120^{\circ} ; \\ B E=B C \\ \Rightarrow \Delta A B E=\Delta D B C \text { (c.g.c) }
Do đó, $A E=D C$ ( 2 cạnh tương ứng).
Bài 5 trang 96
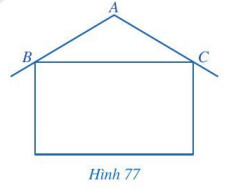
Tính độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong mỗi trường hợp sau:
a) Góc ở đỉnh $A$ là (khoảng) $120^{\circ}$ đối với mái nhà lợp bằng ngói;
b) Góc ở đỉnh $A$ là (khoảng) $140^{\circ}$ đối với mái nhà lợp bằng fibro xi măng;
c) Góc ở đỉnh $A$ là (khoảng) $148^{\circ}$ đối với mái nhà lợp bằng tôn.
Dựa vào tổng ba góc trong một tam giác bằng $180^{\circ}$ để tính độ nghiêng của mái nhà so với mặt phẳng nằm ngang.
Tam giác $A B C$ cân tại A nên $\widehat{B}=\widehat{C}$.
Vậy độ nghiêng của mái nhà so với mặt phẳng nằm ngang bằng: $\left(180^{\circ}-\widehat{A}\right): 2$
a) Góc ở đỉnh $A$ là (khoảng) $120^{\circ}$ đối với mái nhà lợp bằng ngói:
Vậy độ nghiêng của mái nhà so với mặt phẳng nằm ngang bằng: $\left(180^{\circ}-120^{\circ}\right): 2=30^{\circ}$.
b) Góc ở đỉnh $A$ là (khoảng) $140^{\circ}$ đối với mái nhà lợp bằng fibro xi măng:
Vậy độ nghiêng của mái nhà so với mặt phẳng nằm ngang bằng: $\left(180^{\circ}-140^{\circ}\right): 2=20^{\circ}$.
c) Góc ở đỉnh $A$ là (khoảng) $148^{\circ}$ đối với mái nhà lợp bằng tôn:
Vậy độ nghiêng của mái nhà so với mặt phẳng nằm ngang bằng: $\left(180^{\circ}-148^{\circ}\right): 2=16^{\circ}$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Tam giác cân trang 93, 94, 95, 96 Toán 7 Cánh Diều tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





