Giải SGK bài Tổng các góc trong tam giác Toán 7 Cánh Diều tập 2
Trong bài này, HocThatGioi sẽ giúp các bạn giải đáp những câu hỏi cũng như bài tập trong bài Tổng các góc trong tam giác ở các trang 70, 71, 72, 73, 74. Đây là bài học thuộc Bài 1 chương 7 Toán 7 Cánh Diều. Hi vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày bên dưới.
Trả lời câu hỏi SGK bài Tổng các góc tam giác Toán 7 Cánh Diều
Cùng HocThatGioi đi tìm đáp án cho các hoạt động khởi động, thực hành và vận dụng ở các trang 70, 71, 72, 73 trong bài Tổng các góc tam giác Toán 7 Cánh Diều ở ngay bên dưới nhé!
Khởi động trang 70
Xác định phương nằm ngang là phương nào, độ nghiêng của tháp được xác định như nào.
Để biết được độ nghiêng của tòa tháp Capital Gate so với phương nằm ngang ta xác định số đo góc được tạo bới tòa tháp và mặt đất (phương nằm ngang).
Hoạt động 1 trang 70
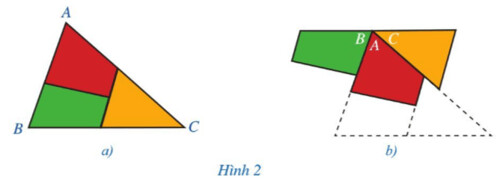
Số góc của bẹt là 180^o
Dự đoán tổng ba góc: \widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}
Luyện tập 1 trang 71
Tổng ba góc trong một tam giác bằng 180^o .
Đặc điểm của tam giác đều: độ dài các cạnh bằng nhau, các góc có số đo bằng nhau.
Số đo mỗi góc của tam giác đều bằng $\frac{180}{3}=60^{\circ}$.
Hoạt động 2 trang 72
Trong tam giác ABC: $\widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}$.
Suy ra $\widehat{B}+\widehat{C}=180^{\circ}-\widehat{A}=180^{\circ}-90^{\circ}=90^{\circ}$.
Vậy $\widehat{B}+\widehat{C}=90^{\circ}$.
Luyện tập 2 trang 72
Xác định đâu là góc (độ nghiêng) tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất).
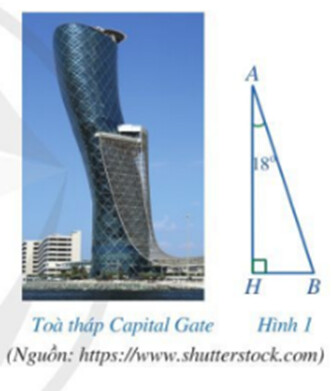
Góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất) là góc $\widehat{B}$.
Ta có:
$\widehat{B}+90^{\circ}+18^{\circ}=180^{\circ}$ (tổng ba góc của một tam giác).
Suy ra: $\widehat{B}=180^{\circ}-90^{\circ}-18^{\circ}=72^{\circ}$
Vậy góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang có số đo là $72^{\circ}$.
Giải bài tập SGK bài Tổng các góc tam giác Toán 7 Cánh Diều
Cùng xem cách HocThatGioi áp dụng các kiến thức về Tổng các góc tam giác ở trên để giải các bài tập cuối bài trong SGK ở trang 72, 73 Toán 7 Cánh Diều như thế nào nhé!
Bài 1 trang 72
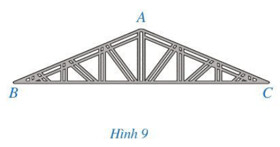
Tổng ba góc trong một tam giác bằng 180°.
Ta có: $\widehat{A}+23^{\circ}+23^{\circ}=180^{\circ}$
Suy ra: $\widehat{A}=180^{\circ}-23^{\circ}-23^{\circ}=134^{\circ}$.
Bài 2 trang 73
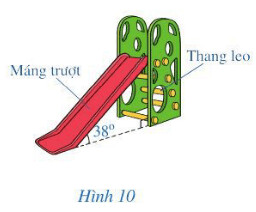
Xác định góc được tạo bởi máng trượt với phương thẳng đứng.
Tổng số đo 3 góc trong một tam giác bằng 180 độ.
Chiếc cầu trượt được minh họa và đặt tên các đỉnh như hình dưới đây:
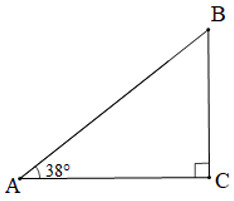
Xét tam giác $A B C$ vuông tại $C$ :
$\widehat{A}+\widehat{B}=90^{\circ}$ (trong tam giác vuông, tổng hai góc nhọn bằng $90^{\circ}$ ). Suy ra $\widehat{B}=90^{\circ}-\widehat{A}=90^{\circ}-38^{\circ}=52^{\circ}$.
Vậy độ nghiêng của máng trượt so với phương thẳng đứng là $52^{\circ}$.
Bài 3 trang 73
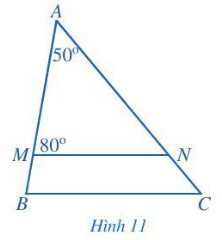
Trong tam giác AMN, tổng số đo của ba góc bằng $180^{\circ}$, suy ra số đo góc ANM.
Sử dụng tính chất 2 đường thẳng song song, suy ra số đo góc $C$.
Vì MN // BC nên $\widehat{A N M}=\widehat{C}$ (2 góc đồng vị)
Áp dụng định lí tổng ba góc trong tam giác AMN có:
\widehat{A}+\widehat{M}+\widehat{A N M}=180^{\circ} \\ \Rightarrow \widehat{A N M}=180^{\circ}-50^{\circ}-80^{\circ}=50^{\circ} .
Vậy $\widehat{C}=50^0$
Bài 4 trang 73
– Làm một thước chữ T như Hình 13;
– Đặt thước chữ T dọc theo cạnh $A B$ như Hình $12, O E \perp A B$;
– Buộc một sợi dây vào chân $O$ của thước chữ $\mathrm{T}$ và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi);
– Tính góc $B A C$, biết rằng dây dọi $O I$ tạo với trục $O E$ của thước chữ T một góc $15^{\circ}$.
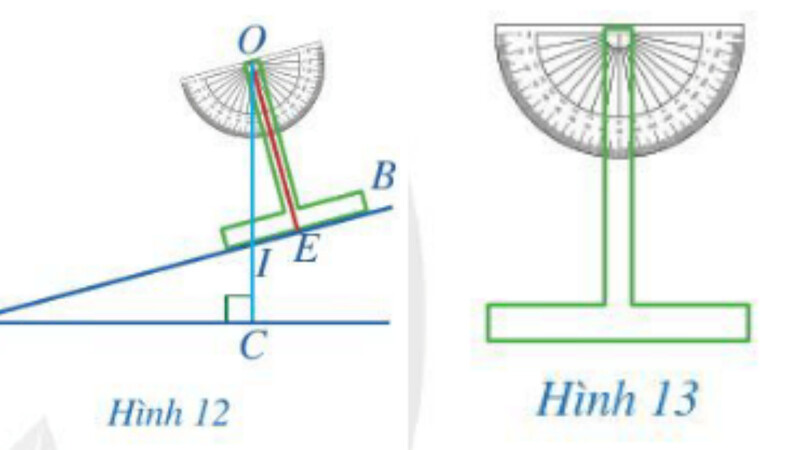
Áp dụng:
+ Định lí Tổng số đo ba góc trong tam giác AIC và OIE.
+ Tính chất hai góc đối đỉnh
Từ đó suy ra mối quan hệ giữa góc BAC và IOE
Trong tam giác OIE: $\widehat{O I E}+\widehat{I O E}+90^{\circ}=180^{\circ}$.
Trong tam giác $A / C: \widehat{A I C}+\widehat{I A C}+90^{\circ}=180^{\circ}$.
Mà $\widehat{O I E}=\widehat{A I C}$ (đối đỉnh)
$\Rightarrow \widehat{I O E}=\widehat{I A C}$. Mà $\widehat{I O E}=15^0$
Vậy góc $B A C$ bằng: $15^{\circ}$.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Tổng các góc trong tam giác Toán 7 Cánh Diều tập 2 ở các trang 70, 71, 72, 73, 74. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





