Giải SGK bài Cộng, trừ, nhân, chia số hữu tỉ chương 1 Toán 7 Cánh diều tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Cộng, trừ, nhân, chia số hữu tỉ. Các bài tập sau đây thuộc bài 2 chương 1 – Số hữu tỉ trang 12, 13, 14, 15, 16 Toán 7 Cánh diều tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Cộng, trừ, nhân, chia số hữu tỉ trang 12, 13, 14, 15, 16
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 12, 13, 14, 15, 16 trong bài Cộng, trừ, nhân, chia số hữu tỉ. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Hoạt động 1 trang 12
a) $\frac{-2}{5}+\frac{3}{7}$
b) $0,123-0,234$
a) Quy đồng mẫu hai phân số rồi thực hiện phép cộng hai phân số.
b) Áp dụng quy tắc trừ hai số thập phân.
a) $\frac{-2}{5}+\frac{3}{7}=\frac{-14}{35}+\frac{15}{35}=\frac{1}{35}$
b) $0,123-0,234=-(0,234-0,123)=-0,111$.
Luyện tập vận dụng 1 trang 13
a) $\frac{5}{7}-(-3,9)$
b) $(-3,25)+4 \frac{3}{4}$
Đưa hai số về phép cộng, trừ hai phân số.
Quy đồng mẫu hai phân số rồi thực hiện phép cộng hai phân số.
a) $\frac{5}{7}-(-3,9)=\frac{5}{7}+3,9=\frac{5}{7}+\frac{39}{10}=\frac{50}{70}+\frac{273}{70}=\frac{323}{70}$;
b) $(-3,25)+4 \frac{3}{4}=-\frac{13}{4}+\frac{19}{4}=\frac{6}{4}=\frac{3}{2}$.
Hoạt động 2 trang 13
Nhớ lại tính chất của phép cộng các số nguyên đã học.
Tính chất giao hoán: $a+b=b+a$.
Tính chất kết hợp: $(a+b)+c=a+(b+c)$.
Cộng với số 0: $a+0=0+a=a$.
Cộng với số đối: $a+(-a)=0$.
Luyện tập vận dụng 2 trang 13
a) $(-0,4)+\frac{3}{8}+(-0,6)$
b) $\frac{4}{5}-1,8+0,375+\frac{5}{8}$
Sử dụng tính chất giao hoán của các số hữu tỉ.
a) $(-0,4)+\frac{3}{8}+(-0,6)=[(-0,4)+(-0,6)]+\frac{3}{8}=-1+\frac{3}{8}=\frac{-5}{8}$.
b)$\frac{4}{5}-1,8+0,375+\frac{5}{8}=(0,8-1,8)+(0,375+0,625)=(-1)+1=0$
Hoạt động 3 trang 13
b) Trong tập hợp các số nguyên, nêu quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.
a) Áp dụng quy tắc tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại.
b) Nhắc lại quy tắc đã được học.
a)
$ x+5=-3 $
$ x=-3-5 $
$ x=-8$
Vậy $x=-8$
b) Quy tắc: Muốn tìm một số hạng của tổng hai số khi biết tổng và số hạng còn lại, ta lấy tổng trừ đi số hạng kia.
Luyện tập vận dụng 3 trang 14
a) $x-\left(-\frac{7}{9}\right)=-\frac{5}{6}$;
b) $\frac{15}{-4}-x=0,3$.
Sử dụng quy tắc chuyển vế.
a)
$ x-\left(-\frac{7}{9}\right)=-\frac{5}{6} $
$ x+\frac{7}{9}=-\frac{5}{6}$
$ x=-\frac{5}{6}-\frac{7}{9} $
$ x=-\frac{15}{18}-\frac{14}{18} $
$x=\frac{-29}{18}$
Vậy $ x=\frac{-29}{18}$
b)
$ \frac{15}{-4}-x=0,3 $
$ x=\frac{15}{-4}-0,3$
$x=-3,75-0,3 $
Vậy $x=-4,05$
Hoạt động 4 trang 14
a) $\frac{1}{8} . \frac{3}{5}$
b) $\frac{-6}{7}:\left(-\frac{5}{3}\right)$
c) $0,6 .(-0,15)$
Câu a và b: áp dụng quy tắc nhân, chia hai phân số.
Câu c: Đưa về dạng phép nhân hai phân số, rồi thực hiện phép tính.
a) $\frac{1}{8} .\frac{3}{5}=\frac{1.3}{8.5}=\frac{3}{40}$
b) $\frac{-6}{7}:\left(-\frac{5}{3}\right)=\frac{-6}{7} . \frac{-3}{5}=\frac{18}{35}$
c) $0,6 .(-0,15)=\frac{6}{10}. \frac{-15}{100}=\frac{-90}{1000}=\frac{-9}{100}$.
Luyện tập vận dụng 4 trang 14
Độ dài đèo Hải Vân = Độ dài hầm Hải Vân : $\frac{157}{500}$
Độ dài đèo Hải Vân là:
$6,28: \frac{157}{500}=\frac{157}{25}.\frac{500}{157}=\frac{3135}{157} \approx 20(\mathrm{~km})$
Luyện tập vận dụng 5 trang 14
Thời gian ô tô đi hết cả quãng đường $\mathrm{AB}=$ Thời gian đi : Quãng đường đi được.
Thời gian ô tô đi hết cả quãng đường $A B$ là: $1: \frac{2}{5}=\frac{5}{2}(h)$
Hoạt động 5 trang 15
Nhớ lại tính chất của phép nhân các số nguyên đã học.
Tính chất giao hoán: $a . b=b . a$.
Tính chất kết hợp: $(a . b) . c=a .(b . c)$.
Nhân với số 1: $a .1=1 . a=a$.
Tính chất phân phối của phép nhân đối với phép cộng: $a .(b+c)=a . b+a . c$.
Luyện tập vận dụng 6 trang 15
a) $\frac{7}{3} \.(-2,5) . \frac{6}{7}$
b) $0,8 . \frac{-2}{9}-\frac{4}{5} . \frac{7}{9}-0,2$.
Tính chất giao hoán: $a .b=b. a$.
Tính chất kết hợp: $(a . b) . c=a .(b . c)$.
Tính chất phân phối của phép nhân đối với phép trừ: $a .(b-c)=a . b-a . c$.
a) $\frac{7}{3}.(-2,5). \frac{6}{7}=\frac{7}{3} . \frac{6}{7} .(-2,5)=2 .(-2,5)=-5$
b)
$ 0,8.\frac{-2}{9}-\frac{4}{5}. \frac{7}{9}-0,2 $
$=\frac{4}{5}.\frac{-2}{9}-\frac{4}{5} .\frac{7}{9}-\frac{2}{10}$
$=\frac{4}{5} .\left(\frac{-2}{9}-\frac{7}{9}\right)-\frac{1}{5} $
$=\frac{4}{5} .(-1)-\frac{1}{5} $
$=\frac{-4}{5}-\frac{1}{5}$
$ =\frac{-5}{5} $
$ =-1$
Hoạt động 6 trang 15
Phân số cần tìm là phân số nhân với phân số $\frac{m}{n}$ được tích bằng 1.
Phân số nghịch đảo của phân số $\frac{m}{n}$ là: $\frac{n}{m}$
Luyện tập vận dụng 7 trang 16
a) $2 \frac{1}{5}$
b) $-13$
a)Đưa hỗn số về phân số rồi tìm số nghịch đảo
Phân số nghịch đảo của phân số $\frac{m}{n}$ là: $\frac{n}{m}(m \neq 0 ; n \neq 0)$
b) Số nghịch đảo của số a là: $\frac{1}{a}(a \neq 0)$.
a)Ta có: $2 \frac{1}{5}=\frac{11}{5}$
Số nghịch đảo của $2 \frac{1}{5}$ là: $\frac{5}{11}$.
b) Số nghịch đảo của -13 là: $\frac{-1}{13}$
Giải bài tập SGK bài Cộng, trừ, nhân, chia số hữu tỉ trang 16
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Cộng, trừ, nhân, chia số hữu tỉ trang 16 sách Toán 7 Cánh diều tập 1 dưới đây nhé!
Bài tập 1 trang 16
a) $\frac{-1}{6}+0,75$
b) $3 \frac{1}{10}-\frac{3}{8}$;
c) $0,1+\frac{-9}{17}-(-0,9)$
Đưa các phép tính về phép cộng, trừ các phân số.
Áp dụng tính chất giao hoán và kết hợp để tính nhanh (nếu có thể).
a) $\frac{-1}{6}+0,75=\frac{-1}{6}+\frac{3}{4}=\frac{-2}{12}+\frac{9}{12}=\frac{7}{12}$;
b) $3 \frac{1}{10}-\frac{3}{8}=\frac{31}{10}-\frac{3}{8}=\frac{124}{40}-\frac{15}{40}=\frac{109}{40}$;
c)
$ 0,1+\frac{-9}{17}-(-0,9)=\frac{1}{10}+\frac{-9}{17}+\frac{9}{10}$
$ =\left(\frac{1}{10}+\frac{9}{10}\right)+\frac{-9}{17}=1+\frac{-9}{17}=\frac{17}{17}+\frac{-9}{17}=\frac{8}{17}$
Bài tập 2 trang 16
a) $5,75 . \frac{-8}{9}$;
b) $2 \frac{3}{8} .(-0,4)$;
c) $\frac{-12}{5}:(-6,5)$
Viết các số thập phân, hỗn số dưới dạng phân số.
a) $5,75 . \frac{-8}{9}=\frac{575}{100} . \frac{-8}{9}=\frac{23}{4}. \frac{-8}{9}=\frac{-46}{9}$
b) $2 \frac{3}{8} .(-0,4)=\frac{19}{8} .\frac{-4}{10}=\frac{19}{8}. \frac{-2}{5}=\frac{-19}{20}$;
c) $\frac{-12}{5}:(-6,5)=\frac{-12}{5}: \frac{-65}{10}=\frac{-12}{5}: \frac{-13}{2}=\frac{-12}{5} . \frac{-2}{13}=\frac{24}{65}$.
Bài tập 3 trang 16
a) $\frac{-3}{10}-0,125+\frac{-7}{10}+1,125$
b) $\frac{-8}{3}. \frac{2}{11}-\frac{8}{3}: \frac{11}{9}$
a) Áp dụng tính chất giao hoán và kết hợp của phép cộng.
b) Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
$a .(b+c)=a . b+a . c$
a)
$ \frac{-3}{10}-0,125+\frac{-7}{10}+1,125$
$ =\left(\frac{-3}{10}+\frac{-7}{10}\right)+(1,125-0,125) $
$=-1+1 $
$ =0$
b)
$\frac{-8}{3} . \frac{2}{11}-\frac{8}{3}: \frac{11}{9}$
$ =\frac{8}{3} . \frac{-2}{11}-\frac{8}{3} . \frac{9}{11} $
$ =\frac{8}{3} .\left(\frac{-2}{11}-\frac{9}{11}\right) $
$ =\frac{-8}{3}. \frac{-11}{11} $
$=\frac{8}{3}.(-1)$
$ =\frac{-8}{3}$
Bài tập 4 trang 16
a) $x+\left(-\frac{1}{5}\right)=\frac{-4}{15}$;
b) $3,7-x=\frac{7}{10}$;
c) $x . \frac{3}{2}=2,4$;
d) $3,2: x=-\frac{6}{11}$.
Viết các số thập phân ở dạng phân số.
a,b) Sử dụng quy tắc chuyển vế đổi dấu để tìm x.
c) Tìm thừa số = tích : thừa số đã biết
d) Tìm số chia = số bị chia : thương
a)
$ x+\left(-\frac{1}{5}\right)=\frac{-4}{15}$
$ x=\frac{-4}{15}+\frac{1}{5}$
$ x=\frac{-4}{15}+\frac{3}{15} $
$ x=\frac{-1}{15}$
Vậy $x=\frac{-1}{15}$.
b)
$ 3,7-x=\frac{7}{10}$
$ x=3,7-\frac{7}{10} $
$x=\frac{37}{10}-\frac{7}{10}$
$ x=\frac{30}{10}$
$ x=3$
Vậy $x=3$.
c)
$x . \frac{3}{2}=2,4$
x. $\frac{3}{2}=\frac{12}{5}$
$x=\frac{12}{5}: \frac{3}{2}$
$x=\frac{12}{5}. \frac{2}{3}$
$x=\frac{8}{5}$
Vậy $x=\frac{8}{5}$
d)
$ 3,2: x=-\frac{6}{11} $
$ \frac{16}{5}: x=-\frac{6}{11} $
$ x=\frac{16}{5}:\left(-\frac{6}{11}\right)$
$ x=\frac{16}{5}. \frac{-11}{6} $
$ x=\frac{-88}{15}$
Vậy $x=\frac{-88}{15}$.
Bài tập 5 trang 16
– Tính số tiền lãi sau 1 năm = Số tiền gốc. $\frac{6,5}{100}$
– Tính số tiền gốc và lãi sau 1 năm
– Tính số tiền rút ra
– Tính số tiền còn lại.
Số tiền lãi sau 1 năm là: $60 . \frac{6,5}{100}=3,9$ (triệu đồng)
Số tiền gốc và lãi của bác Nhi sau 1 năm là:
$60+3,9=63,9$ (triệu đồng)
Số tiền bác Nhi rút ra là: $\frac{1}{3} . 63,9=21,3$ (triệu đồng)
Số tiền còn lại của bác Nhi trong ngân hàng là: 63,9 – 21,3 = 42,6 (triệu đồng).
Bài tập 6 trang 16
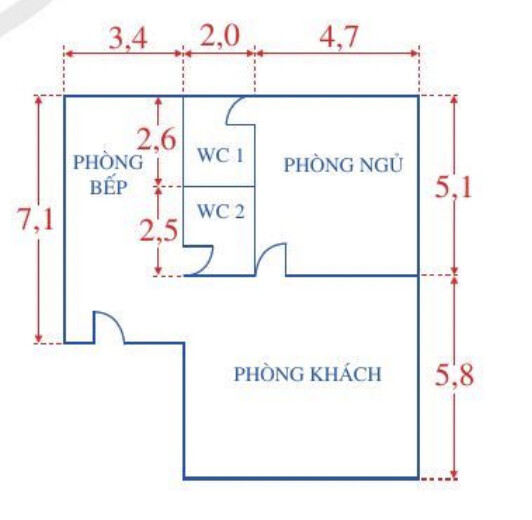
Chia hình thành hai hình chữ nhật rồi tính tổng hai diện tích hai hình chữ nhật đó.
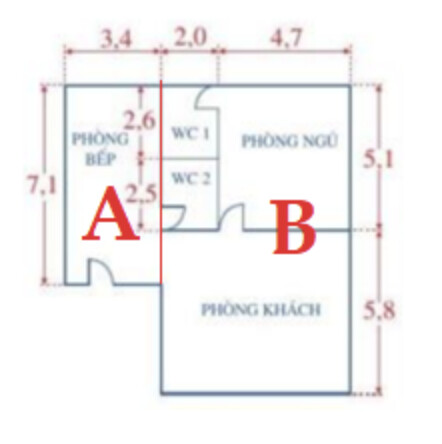
Chia mặt bằng của ngôi nhà thành 2 phần $\mathrm{A}$ và $\mathrm{B}$ như trên.
Diện tích phần A là: $7,1.3,4=24,14\left(m^2\right)$
Chiều dài của phần B là: $5,1+5,8=10,9(m)$
Chiều rộng của phần $B$ là: $2,0+4,7=6,7(m)$
Diện tích phần B là: $10,9.6,7=73,03\left(m^2\right)$
Diện tích mặt bằng của ngôi nhà là:
$24,14+73,03=97,17\left(m^2\right)$
Bài tập 7 trang 16
Khoảng cách trên bản đồ : Khoảng cách thực tế từ ổ cắm điện đến vòi nước = Tỉ lệ bản đồ
Từ đó, tính khoảng cách thực tế từ ổ cắm điện đến vòi nước rồi so sánh với khoảng cách yêu cầu của kiến trúc sư và kết luận.
Theo bản đồ, khoảng cách thực tế từ ổ cắm điện đến vòi nước là:
$2,5: \frac{1}{20}=2,5.20=50(\mathrm{~cm})$
Vì $50 \mathrm{~cm}$ < $60 \mathrm{~cm}$ nên khoảng cách trên bản vẽ như vậy không phù hợp với yêu cầu của kiến trúc sư.
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Cộng, trừ, nhân, chia số hữu tỉ chương 1 –Số hữu tỉ trang 12, 13, 14, 15, 16 Toán 7 Cánh diều tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





