Giải SGK bài Đại lượng tỉ lệ nghịch chương 2 Toán 7 Cánh diều tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, vận dụng, bài tập trong bài Đại lượng tỉ lệ nghịch. Các bài tập sau đây thuộc bài 8 chương 2 – Số thực trang 64, 65, 66, 67, 68 Toán 7 Cánh diều tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Đại lượng tỉ lệ nghịch
Dưới đây là phương pháp và bài giải chi tiết cho các câu hỏi, hoạt động khám phá, thực hành cùng phần luyện tập ở các trang 64, 65, 66, 67 trong bài Đại lượng tỉ lệ nghịch. Cùng HocThatGioi đi tìm đáp án ngay nhé!
Câu hỏi khởi động trang 64
Khi số công nhân tăng lên thì thời gian hoàn thành công việc sẽ tăng lên hay giảm đi?
27 công nhân hoàn thành công việc đó trong bao lâu?
Cách 1: + Tính khối lượng công việc 1 người làm được trong 1 ngày
+ Tính khối lượng công việc 27 người làm được trong 1 ngày
+ Thời gian 27 người làm xong = 1 : khối lượng 27 người làm được trong 1 ngày
Cách 2: Thời gian hoàn thành và số công nhân là hai đại lượng tỉ lệ nghịch.
Khi số công nhân tăng lên thì thời gian hoàn thành giảm đi.
Cách 1: Trong 1 ngày, 18 công nhân làm được: $\frac{1}{12}$ (công việc)
Trong 1 ngày, 1 công nhân làm được: $\frac{1}{12}: 18=\frac{1}{216}$ (công việc)
Trong 1 ngày, 27 công nhân làm được: $\frac{1}{216} .27=\frac{1}{8}$ (công việc)
27 công nhân hoàn thành công việc đó trong: $1: \frac{1}{8}=8$ (ngày)
Cách 2:
Gọi thời gian để 27 công nhân hoàn thành công việc là $x$ (ngày) $(x>0)$
Vì thời gian hoàn thành và số công nhân là 2 đại lượng tỉ lệ nghịch nên theo tính chất 2 đại lượng tỉ lệ nghịch, ta có:
12. $18=x .17$ nên $x=\frac{12.18}{27}=8$
Vậy 27 công nhân hoàn thành công việc trong 8 ngày.
Hoạt động 1 trang 64

Thay giá trị của t vào công thức $v=\frac{240}{t}$ để tính giá trị $v$ tương ứng.
Với $ t=3 \text { thì } v=\frac{240}{3}=80$
Với $ t=4 \text { thì } v=\frac{240}{4}=60 $
Với $ t=5 \text { thì } v=\frac{240}{5}=48$
Với $ t=6 \text { thì } v=\frac{240}{6}=40$

Luyện tập vận dụng 1 trang 65
a) Gọi x (h) là thời gian người công nhân đó làm và y là số sản phẩm làm được trong 1 giờ. Viết công thức tính $\mathrm{y}$ theo $\mathrm{x}$.
b) Hỏi x và y có phải là hai đại lượng tỉ lệ nghịch hay không? Nếu có hãy xác định hệ số tî lệ.
c) Tính giá trị của $y$ khi $x=10 ; x=20 ; x=25$.
b) Nếu đại lượng y liên hệ với đại lượng $x$ theo công thức $y=\frac{a}{x}$ hay $x . y=a$ (a là hằng số khác 0) thì y tỉ lệ nghịch với $x$ theo hệ số tỉ lệ a
c) Thay giá trị $x$ vào công thức liên hệ, tìm $y$.
a) $y=\frac{1000}{x}$
b) $x$ và $y$ là hai đại lượng tỉ lệ nghịch vì $\mathrm{x}$ và $\mathrm{y}$ liên hệ với nhau theo công thức $\mathrm{y}=\frac{1000}{x}$
Hệ số tỉ lệ là: 1000
c) Khi $x=10$ thì $y=\frac{1000}{10}=100$
Khi $x=20$ thì $y=\frac{1000}{20}=50$
Khi $\mathrm{x}=25$ thì $\mathrm{y}=\frac{1000}{25}=40$
Hoạt động 2 trang 65
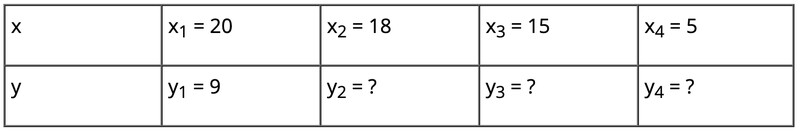
a) Hãy xác định hệ số tỉ lệ
b) Tìm số thích hợp cho ? trong bảng trên
c) So sánh các tỉ số: $\mathrm{x}_1 \mathrm{y}_1 ; \mathrm{x}_2 \mathrm{y}_2 ; \mathrm{x}_3 \mathrm{y}_3 ; \mathrm{x}_4 \mathrm{y}_4$.
d) So sánh các tỉ số: $\frac{x_1}{x_2}$ và $\frac{y_2}{y_1} ; \frac{x_1}{x_3}$ và $\frac{y_3}{y_1} ; \frac{x_3}{x_4}$ và $\frac{y_4}{y_3}$.
+ Nếu đại lượng y liên hệ với đại lượng $x$ theo công thức $y=\frac{a}{x}$ hay x.y = a (a là hằng số khác 0) thì y tỉ lệ nghịch với $x$ theo hệ số tỉ lệ a
+ Tính các tích rồi so sánh
+ Tính các tỉ số rồi so sánh
a) Hệ số tỉ lệ $a=x_1 . y_1=20 .9=180$
b) Ta có: $\mathrm{y}=\frac{180}{x}$
Khi $x_2=18$ thì $\mathrm{y}_2=\frac{180}{x_2}=\frac{180}{18}=10$
Khi $x_3=15$ thì $\mathrm{y}_3=\frac{180}{x_3}=\frac{180}{15}=12$
Khi $\mathrm{x}_4=18$ thì $\mathrm{y}_4=\frac{180}{x_4}=\frac{180}{5}=36$
\begin{aligned}
c) Tích $ \mathrm{x}_1 . \mathrm{y}_1=20 . 9=180 $
$\mathrm{x}_2 . \mathrm{y}_2=18. 10=180 $
$ \mathrm{x}_3 . \mathrm{y}_3=15 . 12=180$
$ \mathrm{x}_4 . \mathrm{y}_4=5.36=180 $
Vậy $ \mathrm{x}_1 \mathrm{y}_1=\mathrm{x}_2 \mathrm{y}_2=\mathrm{x}_3 \mathrm{y}_3=\mathrm{x}_4 \mathrm{y}_4=180$
d) Ta có:
$ \frac{x_1}{x_2}=\frac{20}{18}=\frac{10}{9} ; \frac{y_2}{y_1}=\frac{10}{9}$
$ \frac{x_1}{x_3}=\frac{20}{15}=\frac{4}{3} ; \frac{y_3}{y_1}=\frac{12}{9}=\frac{4}{3}$
$ \frac{x_3}{x_4}=\frac{15}{5}=3 ; \frac{y_4}{y_3}=\frac{36}{12}=3 $
Vậy $ \frac{x_1}{x_2}=\frac{y_2}{y_1} ; \frac{x_1}{x_3}=\frac{y_3}{y_1} ; \frac{x_3}{x_4}=\frac{y_4}{y_3}$
Luyện tập vận dụng 2 trang 66
Thời gian ô tô đi và vận tốc đi trên cùng 1 quãng đường là 2 đại lượng tỉ lệ nghịch
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: $\frac{x_1}{x_2}=\frac{y_2}{y_1}$
Vì $v. t = s$ không đổi nên vận tốc và thời gian ô tô đi là 2 đại lượng tỉ lệ nghịch
Theo tính chất 2 đại lượng tỉ lệ nghịch, ta có:
$\frac{\mathrm{t}_{\text {dự định }}}{\mathrm{t}_{\text {thực tế }}}=\frac{\mathrm{v}_{\text {thực tế }}}{\mathrm{v}_{\text {dự định }}}=\frac{4}{3}$
$ \Rightarrow \mathrm{t}_{\text {thực tế }}=\frac{\mathrm{t}_{\text {dự định }} \cdot 3}{4}=\frac{6.3}{4}=4,5 \text { giờ }$
Luyện tập vận dụng 3 trang 67
+) Số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: $x_1 \cdot y_1=x_2 \cdot y_2$
+) Số công nhân cần tăng thêm = số công nhân cần – số công nhân có sẵn
Gọi số công nhân cần để hoàn thành hợp đồng trong 14 ngày là $x(x>0)$
Vì khối lượng công việc không đổi và năng suất của mỗi người là như nhau nên số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên theo tính chất của 22 đại lượng tỉ lệ nghịch, ta có: $56.21=x .14$ nên $x=\frac{56.21}{14}=84$
Số công nhân cần tăng thêm là:
$84-56=28$ (người)
Luyện tập vận dụng 4 trang 67
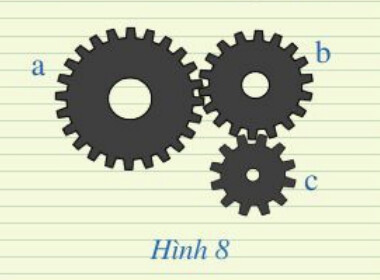
Số răng và số vòng quay được của bánh răng là 2 đại lượng tỉ lệ nghịch
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: $x_1. y_1=x_2 . y_2=x_3 . y_3$
Vì quãng đường quay được của 3 bánh răng là như nhau nên số răng và số vòng quay được của bánh răng là hai đại lượng tỉ lệ nghịch
Gọi số vòng quay được trong 1 phút của bánh răng b và c lần lượt là $x, y$ (vòng) $(x, y$ $>0)$
Theo tính chất của 2 đại lượng tỉ lệ nghịch, ta có:
12. $18=24. x=18 .t y$
Nên x $=12.18: 24=9$ (vòng)
$y=12.18: 18=12$ (vòng)
Vậy số vòng quay trong một phút của mỗi bánh răng b và c lần lượt là: $9$ vòng và $12$ vòng.
Giải bài tập SGK bài Đại lượng tỉ lệ nghịch
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Đại lượng tỉ lệ nghịch trang 68 sách Toán 7 Cánh diều tập 1 dưới đây nhé!
Bài tập 1 trang 68

Cho biết hai đại lượng x,y có tỉ lệ nghịch với nhau không? Vì sao?
Nếu đại lượng y liên hệ với đại lượng $x$ theo công thức $y=\frac{a}{x}$ hay $x.y = a$ (a là hằng số khác 0) thì $y$tỉ lệ nghịch với $x$ theo hệ số tỉ lệ $a$.
2 đại lượng x và y có tỉ lệ nghịch với nhau vì $3.32=4.24=6.16=8.12=48. 2$
Bài tập 2 trang 68
a) Tìm hệ số tỉ lệ.
b) Viết công thức tính $\mathrm{y}$ theo $x$
c) Tính giá trị của $y$ khi $x=12 ; x=18 ; x=60$.
+ Nếu đại lượng y liên hệ với đại lượng $x$ theo công thức $y=\frac{a}{x}$ hay $x . y=a$ (a là hằng số khác 0) thì y tỉ lệ nghịch với $x$ theo hệ số tỉ lệ a
+ Thay giá trị của $x$ vào công thức liên hệ, tìm giá trị y tương ứng.
a) Hệ số tỉ lệ là: $a=x . y=36.15=540$
b) Công thức tính $\mathrm{y}$ theo $\mathrm{x}$ là: $\mathrm{y}=\frac{a}{x}=\frac{540}{x}$
c) Khi $x=12$ thì $y=\frac{540}{12}=45$
Khi $\mathrm{x}=18$ thì $\mathrm{y}=\frac{540}{18}=30$
Khi $x=60$ thì $y=\frac{540}{60}=9$
Bài tập 3 trang 68
Số thợ và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: $x_1. y_1=x_2 . y_2$
Gọi thời gian để nhóm thợ hoàn thành công việc là $x$ (ngày) $(x>0)$
Vì khối lượng công việc không đổi và năng suất làm việc của mỗi người là như nhau nên số thợ và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Áp dụng tính chất của 2 đại lượng tỉ lệ nghịch, ta có:
$35.168=28 . x$ nên $x=35.168: 28=210$ (thỏa mãn)
Vậy, nhóm thợ phải mất 210 ngày để xây xong tòa nhà.
Bài tập 4 trang 68
Số hoa mua được và giá hoa là 2 đại lượng tỉ lệ nghịch.
Sử dụng tính chất của hai đại lượng tỉ lệ nghịch: $x_1 . y_1=x_2 . y_2$
Gọi số hoa mua được là x (bông) $\left(x \in \mathbb{N}^*\right.$ )
Giả sử giá hoa trước lễ là a thì giá hoa vào dịp lễ là 1,25.a
Vì số hoa . giá hoa = số tiền mua hoa (không đổi) nên số hoa và giá hoa là hai đại lượng tỉ lệ nghịch.
Áp dụng tính chất của 2 đại lượng tỉ lệ nghịch, ta có:
10. $a=x .1,25 . a$ nên $x=\frac{10. a}{1,25. a}=8$ (thỏa mãn)
Vậy chị Lan mua được 8 bông hoa.
Bài tập 5 trang 68
Cũng ở nội dung bơi 400 m nữ tại Giải bơi lội vô địch thế giới tổ chức tại Kazan (Nga) năm 2015, Ánh Viên đạt thành tích là 4 phút 38 giây 78( tức là 4 phút và 38,78 giây).
Tính tỉ số giữa tốc độ trung bình của Ánh Viên tại Thế vận hội mùa hè năm 2016 và tại Giải bơi lội vô địch thế giới tổ chức ở Kazan (Nga) năm 2015
Đổi đơn vị về giây
Vận tốc và thời gian đi cùng quãng đường là 2 đại lượng tỉ lệ nghịch
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: $\frac{x_1}{x_2}=\frac{y_2}{y_1}$
Đổi 4 phút 36 giây $85=276,85$ giây
4 phút 38 giây $78=278,78$ giây
Vì quãng đường không đổi nên vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch
Áp dụng tính chất 2 đại lượng tỉ lệ nghịch, ta có:
$\frac{v_1}{v_2}=\frac{t_2}{t_1}=\frac{278,78}{276,85} \approx 1,007$
Vậy tỉ số giữa tốc độ trung bình của Ánh Viên tại Thế vận hội mùa hè năm 2016 và tại Giải bơi lội vô địch thế giới tổ chức ở Kazan (Nga) năm 2015 là: $1,007$
Bài tập 6 trang 68
Nếu tàu cao tốc loại đó chạy một quãng đường trong 4 giờ thì tàu cao tốc thế hệ đầu tiên sẽ phải chạy quãng đường đó trong bao nhiêu giờ?
Vận tốc và thời gian đi cùng quãng đường là 2 đại lượng tỉ lệ nghịch
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: $\frac{x_1}{x_2}=\frac{y_2}{y_1}$
Gọi $t_1$ $v_1$ lần lượt là thời gian và vận tốc của thế hệ tàu cao tốc đầu tiên.
$t_2, v_2$ lần lượt là thời gian và vận tốc của cao tốc hiện nay.
Vì quãng đường không đổi nên vận tốc và thời gian là 2 đại lượng tỉ lệ nghịch.
Áp dụng tính chất 2 đại lượng tỉ lệ nghịch, ta có:
$\frac{v_2}{v_1}=\frac{t_1}{t_2}$
Mà tàu hiện nay đi với vận tốc gấp 1,43 lần so với thế hệ tàu cao tốc đầu tiên nên $\frac{v_2}{v_1}=1,43$
Ta được: $\frac{t_1}{4}=1,43 \Rightarrow t_1=1,43.4=5,72(\mathrm{~h})$.
Vậy nếu tàu cao tốc loại đó chạy một quãng đường trong 4 giờ thì tàu cao tốc thế hệ đầu tiên sẽ phải chạy quãng đường đó trong $5,72$ giờ.
Bài tập 7 trang 68
Số răng và số vòng quay được của bánh răng là 2 đại lượng tỉ lệ nghịch
Sử dụng tính chất 2 đại lượng tỉ lệ nghịch: $x_1 . y_1=x_2. y_2=x_3 . y_3$
Vì quãng đường quay được của 2 bánh răng là như nhau nên số răng và số vòng quay được của bánh răng là hai đại lượng tỉ lệ nghịch
Gọi số răng của bánh răng thứ hai là $x(x>0)$
Theo tính chất của 2 đại lượng tỉ lệ nghịch, ta có:
$40.15 = x. 20$ nên $x =40.15:20=30$ (thỏa mãn)
Vậy bánh răng thứ hai có 30 răng
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Đại lượng tỉ lệ nghịch chương 2 – Số thực trang 64, 65, 66, 67, 68 Toán 7 Cánh diều tập 1. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





