Giải SGK Bài 1 Chương 6 trang 40, 41, 42, 43, 44, 45, 46 Toán 7 Cánh diều tập 2
Trong bài viết này, HocThatGioi sẽ giải đáp những câu hỏi và bài tập trong bài Biểu thức số, Biểu thức đại số. Đây là bài học thuộc Bài 1 Chương VI trang 40, 41, 42, 43, 44, 45, 46 sách Toán 7 Cánh diều tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài 1 chương 6 Toán 7 Cánh diều tập 2
Khởi động bài học với những câu hỏi hoạt động và luyện tập vận dụng sẽ giúp bạn dễ dàng tiếp thu kiến thức về bài học Biểu thức số, biểu thức đại số.
Hoạt động 1 trang 40
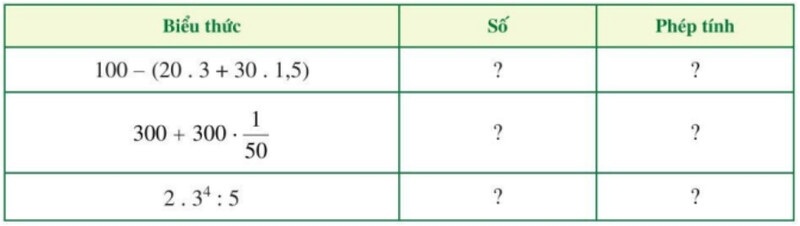
Quan sát biểu thức có trong bảng để đưa ra số và phép tính.
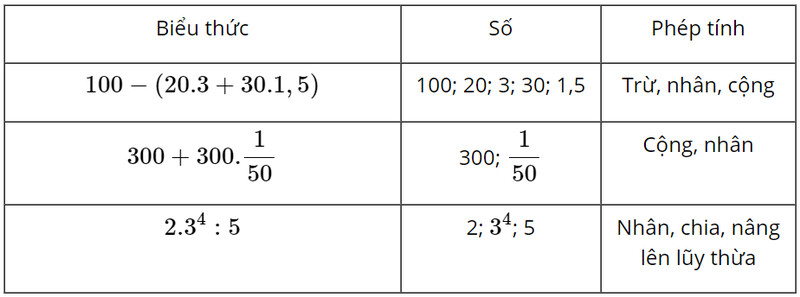
Luyện tập vận dụng 1 trang 40
a) 12.a không phải là biểu thức số.
b) Biểu thức số phải có đầy đủ các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa.
Các số được nối với nhau bởi dấu các phép tính (cộng, trừ, nhân, chia, nâng lên lũy thừa) tạo thành một biểu thức số.
Mỗi số cũng là một biểu thức số.
a) Đúng.
b) Sai.
Luyện tập vận dụng 2 trang 41
a) Diện tích của hình tam giác có độ dài cạnh đáy là 3 cm, chiều cao tương ứng là 5 cm;
b) Diện tích hình tròn có bán kính là 2 cm.
a) Nhớ lại công thức tính diện tích tam giác (bằng đáy nhân chiều cao chia hai).
b) Nhớ lại công thức tính diện tích hình tròn (bằng pi (3,14) nhân bán kính bình phương).
a) Biểu thức số biểu thị diện tích của hình tam giác có độ dài cạnh đáy là 3cm, chiều cao tương ứng là 5cm là: $\frac{1}{2}.3.5$ ($cm^2$)
b) Biểu thức số biểu thị diện tích của hình tròn có bán kính là 2cm là: $3,14.2^2$ ($cm^2$)
Luyện tập vận dụng 3 trang 42
Các số, biến số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa làm thành một biểu thức đại số.
Các biến số như x, y, a, b, c, …
Biểu thức đại số: $2x+1$ (biến số là $x$)
Biểu thức đại số: $x.(3+y).(z-2)$ (biến số là $x, y, z$)
…
Luyện tập vận dụng 4 trang 43
Các bạn lớp 7A quyên góp tiền mua vở và bút bi để ủng hộ học sinh vùng lũ lụt. Giá mỗi quyển vở là 6000 đồng, giá mỗi chiếc bút bi là 3000 đồng.
Nếu mua 15 quyển vở và 10 chiếc bút bi thì hết 120000 đồng.
Nếu mua 12 quyển vở và 18 chiếc bút bi thì hết 126000 đồng.
Có thể sử dụng một biểu thức để biểu thị số tiền mua a quyển vở và b chiếc bút bi được không?
Biểu thức đại số được tạo thành từ các số, biến số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa.
Giá mỗi quyển vở là 6000 đồng, vậy số tiền mua a quyển vở là: $6000a$ (đồng).
Giá mỗi chiếc bút bi là 3000 đồng, vậy số tiền mua b chiếc bút bi là: $3000b$ (đồng).
Biểu thức để biểu thị số tiền mua a quyển vở và b chiếc bút bi là: $6000a+3000b$ (đồng).
Vậy có thể sử dụng một biểu thức để biểu thị số tiền mua a quyển vở và b chiếc bút bi.
Luyện tập vận dụng 5 trang 43
a) Tích của tổng x và y với hiệu của x và y;
b) Ba phẩy mười bốn nhân với bình phương của r.
Biểu thức đại số được tạo thành từ các số, biến số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa.
Trong biểu thức đại số có thể có các dấu ngoặc để chỉ thứ tự thực hiện các phép tính.
a) Tổng $x$ và $y$ là: $x+y$
Hiệu $x$ và $y$ là: $x-y$
Vậy, biểu thức đại số biểu thị tích của tổng $x$ và $y$ với hiệu của $x$ và $y$ là: $(x+y) .(x-y)$.
b) Biểu thức đại số biểu thị ba phẩy mười bốn nhân với bình phương của r là: $3,14 . x^2$
Luyện tập vận dụng 6 trang 43
Để tính giá trị của một biểu thức đại số tại những giá trị cho trước của các biến, ta thay những giá trị cho trước đó vào biểu thức rồi thực hiện phép tính.
Với bài tập trên, ta thay $x=10, y=-3$ vào biểu thức đã cho rồi thực hiện phép tính.
Thay giá trị $x=10, y=-3$ vào biểu thức đã cho, ta có:
$D=-5 x y^2+1=-5.10 .(-3)^2+1=-50.9+1=-450+1=-449$
Luyện tập vận dụng 7 trang 44
b) Nếu $x \neq 0$ thì $-x^2$ và $(-x)^2$ có bằng nhau không?
Để tính giá trị của một biểu thức đại số tại những giá trị cho trước của các biến, ta thay những giá trị cho trước đó vào biểu thức rồi thực hiện phép tính.
a) Ta thay $x=-3$ vào biểu thức đã cho rôi thực hiện phép tính.
b) Muốn so sánh nếu $x \neq 0$ thì $-x^2$ và $(-x)^2$ có bằng nhau không, ta có thể tính hoặc thay một giá trị bất kì của $x$ thỏa mãn điều kiện đã cho vào hai biểu thức rồi so sánh kết quả phép tính.
a) Thay giá trị $x=-3$ vào biểu thức đã cho, ta có:
$S=-x^2=-3^2=-9$
b) Ta thấy, nếu $x \neq 0$ thì: $-x^2=-x^2$ và $(-x)^2=x^2$
Vậy nếu $x \neq 0$ thì $-x^2$ và không bằng nhau.
Giải bài tập SGK bài 1 chương 6 Toán 7 Cánh diều tập 2
Sau khi đã tìm hiểu phần nội dung của bài học, cùng ôn lại những kiến thức đã học qua phần giải đáp chi tiết các bài tập trong SGK Toán 7 Cánh diều tập 2 trang 45, 46 dưới đây nhé.
Bài tập 1 trang 45
a) $2.5+6 (\mathrm{cm})$
b) $2.(5+6) (\mathrm{cm})$.
Áp dụng công thức tính chu vi hình chữ nhật: $P=2.(a+b)$ (trong đó a là chiều dài và b là chiều rộng, cùng đơn vị đo).
Biểu thức b) $2.(5+6) (\mathrm{cm})$ dùng để biểu thị chu vi hình chữ nhật đó.
Bài tập 2 trang 45
Áp dụng công thức khai triển của $(a+b)^5=a^5+5 a^4 b+10 a^3 b^2+10 a^2 b^3+5 a b^4+b^5$
Ta có:
$(2 x+3)^5=32 x^5+240 x^4+720 x^3+1080 x^2+810 x+243$
Hệ số của $x^3$ là $720$
Hệ số của $x^4$ là $240$
Vậy hệ số của $x^3$ lớn hơn hệ số của $x^4$.
Bài tập 3 trang 45
Muốn xem bạn nào đúng, ta thay $x=-1$ và $y=-2$ vào các biểu thức $A, B, C$ rồi thực hiện phép tính. Sau đó, so sánh kết quả của 3 biểu thức.
Thay giá trị $x=-1$ và $y=-2$ vào các biểu thức đã cho, ta có:
$A=-(-4 x+3 y)=-(-4 .-1+3 .-2)=-(4+-6)=-(-2)=2$
$B=4 x+3 y=4 .-1+3 .-2=-4+-6=-10$
$C=4 x-3 y=4 .(-1)-3 .(-2)=-4–6=-4+6=2$
Ta thấy $2 \neq-2=2$.
Do vậy, khi thay giá trị $x=-1$ và $y=-2$ vào các biểu thức đã cho ta thấy giá trị của các biểu thức $A$ và $C$ bằng nhau.
Vậy bạn Bình nói đúng.
Bài tập 4 trang 45
a) Viết biểu thức tính số tiền khi mua $x$(kg) nho đỏ Red Cardinal, $y$(kg) nho xanh NH01-48 và $t$(kg) nho ba màu NH01-152.
b) Tính số tiền khi mua 300kg nho đỏ Red Cardinal, 250kg nho xanh NH01-48 và 100kg nho ba màu NH01-152.

Biểu thức đại số được tạo thành từ các số, biến số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa.
Trong biểu thức đại số có thể có các dấu ngoặc để chỉ thứ tự thực hiện các phép tính.
a) Ta viết biểu thức tính số tiền khi mua từng loại nho (bằng số tiền nhân với số kg mua) rồi cộng lại với nhau.
b) Thay các giá trị (số kg mua) vào biểu thức rồi thực hiện phép tính.
a) Biểu thức tính số tiền khi mua $x(\mathrm{kg})$ nho đỏ Red Cardinal: $45000 x$ (đồng).
Biểu thức tính số tiền khi mua $y(\mathrm{kg})$ nho xanh NH01-48: $70000 y$ (đồng).
Biểu thức tính số tiền khi mua $t(\mathrm{kg}$ ) nho ba màu NH01-152: $140000 t$ (đồng).
Vậy biểu thức tính số tiền khi mua $x(\mathrm{kg})$ nho đỏ Red Cardinal, $y(\mathrm{kg})$ nho xanh NH01-48 và $t(\mathrm{kg})$ nho ba màu NH01-152 là:
$45000 x+70000 y+140000t$ (đồng)
b) Số tiền khi mua 300kg nho đỏ Red Cardinal, 250kg nho xanh NH01-48 và 100kg nho ba màu NH01-152 là:
$45000.300+70000.250+140000.100=13500000+17500000+14000000=45000000$ (đồng)
Bài tập 5 trang 46
a) Viết biểu thức biểu thị:
– Giá tiền của 1 cốc trà sữa sau khi giảm giá;
– Số tiền mua 5 cốc trà sữa sau khi giảm giá;
– Số tiền mua 3 lọ sữa chua.
b) Bạn Quân mang theo 195 000 đồng. Số tiền này vừa đủ để mua lượng trà sữa và sữa chua như dự định (khi chưa giảm giá). Giá tiền của một cốc trà sữa sau khi đã giảm giá là bao nhiêu? Biết giá một lọ sữa chua là 15 000 đồng.
a) Viết biểu thức biểu thị các đại lượng.
(giá tiền 1 cốc trà sữa sau khi giảm giá = số tiền ban đầu – số tiền được giảm).
b) Viết biểu thức biểu thị số tiền vừa đủ để mua lượng trà sữa và sữa chua như dự định (khi chưa giảm giá) để tính số tiền một cốc trà sữa khi chưa giảm giá.
Sau đó ta tính số tiền của một cốc trà sữa sau khi giảm giá.
a) Giá bán trà sữa mà bạn Quân dự định mua đã giảm $10 \%$, số tiền mà bạn Quân được giảm là:
$\frac{x.10}{100}=\frac{x}{10}$ (đồng).
Biểu thức biểu thị:
– Giá tiền của 1 cốc trà sữa sau khi giảm giá là $x-\frac{x}{10}=\frac{10x-x}{10}=\frac{9x}{10}=\frac{9}{10} x$ (đồng).
– Số tiền mua 5 cốc trà sữa sau khi giảm giá là $5.\frac{9}{10} x=\frac{9}{2} x$ (đồng).
– Số tiền mua 3 lọ sữa chua là $3 y$.
b) Biểu thức biểu thị số tiền vừa đủ để mua lượng trà sữa và sữa chua như dự định (khi chưa giảm giá) là:
$5 x+3 y=195000=5 x+3.15000=195000$
$\Rightarrow 5 x+45000=195000$ $\Rightarrow 5 x=150000$ $\Rightarrow x=30000$
Vậy giá tiền của một cốc trà sữa khi chưa giảm giá là $30000$ đồng.
Giá tiền của một cốc trà sữa sau khi đã giảm giá là: $\frac{9}{10} .30000=27000$ (đồng).
Bài tập 6 trang 46
b) Cô Ngân gửi ngân hàng 200 triệu đồng với lãi suất $6\%$/năm. Hết kì hạn 1 năm, cô Ngân nhận được số tiền lãi là bao nhiêu?
a) Số tiền lãi khi hết kì hạn một năm bằng số tiền gửi ngân hàng nhân với lãi suất rồi chia cho 100.
b) Thay các giá trị tương ứng vào biểu thức phần a rồi thực hiện phép tính.
a) Biểu thức đại số biểu thị số tiền lãi khi hết kì hạn 1 năm nếu gửi ngân hàng $A$ đồng là:
$\frac{A . r}{100}$ (đồng)
b) Cô Ngân gửi ngân hàng 200 triệu đồng với lãi suất $6\%$/năm. Hết kì hạn 1 năm, cô Ngân nhận được số tiền lãi là:
$\frac{200.6}{100}=12$ (triệu đồng)
Bài tập 7 trang 46
Chiều cao của con trai $=\frac{1}{2} .1,08(b+m);$
Chiều cao của con gái $=\frac{1}{2}(0,923 b+m)$
(Nguồn: https://vietnamnet.vn)
Theo cách ước tính trên, nếu bố cao $170 \mathrm{cm}$, mẹ cao $160 \mathrm{cm}$ thì chiều cao ước tính của con trai, con gái khi trưởng trành là bao nhiêu?
Thay chiều cao của bố và của mẹ vào biểu thức rồi thực hiện phép toán để ra chiều cao ước tính của con trai, con gái khi trưởng thành.
Theo cách ước tính trên, nếu bố cao $170 \mathrm{cm}$, mẹ cao $160 \mathrm{cm}$ thì chiều cao ước tính của con trai, con gái khi trưởng trành là:
Chiều cao của con trai $=\frac{1}{2} . 1,08(b+m)=\frac{1}{2}. 1,08 .(170+160)=\frac{1}{2} . 1,08 . 330=178,2(\mathrm{cm})$
Chiều cao của con gái $=\frac{1}{2}(0,923 b+m)=\frac{1}{2}.(0,923 . 170+160)=\frac{1}{2} .(156,91+160)=158,455 (\mathrm{cm})$
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Bài 1 Chương VI Biểu thức đại số trang 40, 41, 42, 43, 44, 45, 46 sách Toán 7 Cánh diều tập 2. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn học tốt!





