Giải SGK Bài 3 Chương 6 trang 54, 55, 56, 57, 58, 59 Toán 7 Cánh diều tập 2
Trong bài viết này, HocThatGioi sẽ giải đáp những câu hỏi và bài tập trong bài Phép cộng, phép trừ đa thức một biến. Đây là bài học thuộc Bài 3 Chương VI trang 54, 55, 56, 57, 58, 59 sách Toán 7 Cánh diều tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK Bài 3 Chương 6 Toán 7 Cánh diều tập 2
Khởi động bài học với những câu hỏi hoạt động và luyện tập vận dụng sẽ giúp bạn dễ dàng tiếp thu kiến thức về bài học Phép cộng, phép trừ đa thức một biến.
Câu hỏi khởi động trang 54
Phép cộng, phép trừ hai đa thức một biến được thực hiện như thế nào?
Đọc lại bài (Phần I để xem cách cộng hai đa thức và phần II để xem cách trừ hai đa thức).
a) Cộng hai đa thức:
Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
– Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Viết tổng hai đơn thức theo hàng ngang;
– Nhóm các đơn thức có cùng số mũ của biến với nhau;
– Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
b) Trừ hai đa thức:
Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
– Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;
– Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;
– Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Hoạt động 1 trang 54
b) Nêu quy tắc cộng hai đơn thức có cùng số mũ của biến.
a) Để thực hiện phép cộng trong các phép tính, ta giữ nguyên biến và cộng các hệ số lại với nhau.
b) Rút ra quy tắc cộng hai đơn thức có cùng số mũ của biến từ cách thực hiện phần a.
a) $5 x^2+7 x^2=(5+7) x^2=12 x^2;$
$a x^2+b x^2=(a+b) x^2$
b) Muốn cộng hai đơn thức có cùng số mũ của biến, ta giữ nguyên biến và tính tổng của các hệ số có trong đơn thức.
Hoạt động 2 trang 54
$P(x)=5 x^2+4+2 x$ và $Q(x)=8 x+x^2+1 $
a) Sắp xếp các đa thức $P(x), Q(x)$ theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của $P(x)$ và $Q(x)$ cho ? ở bảng sau rồi cộng hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
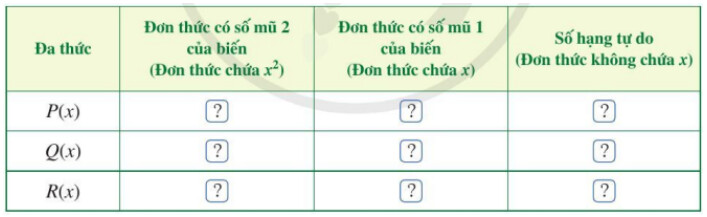
c) Dựa vào kết quả cộng hai đơn thức theo từng cột, xác định đơn thức $R(x)$.
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Quan sát bảng để đưa ra các đơn thức thích hợp phù hợp với biến có số mũ tương ứng.
c) Xác định đơn thức $R(x)$ dựa vào kết quả phần b).
a) $P(x)=5 x^2+4+2 x=5 x^2+2 x+4$
$Q(x)=8 x+x^2+1=x^2+8 x+1$
b)
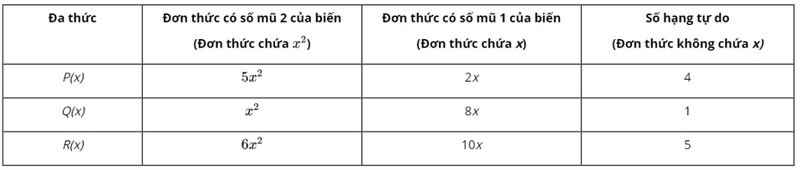
c) Vậy $R(x)=6 x^2+10 x+5$.
Hoạt động 3 trang 56
$P(x)=-2 x^2+1+3 x$ và $Q(x)=-5 x+3 x^2+4$
a) Sắp xếp các đa thức $P(x)$ và $Q(x)$ theo số mũ giảm dần của biến.
b) Viết tổng $P(x)+Q(x)$ theo hàng ngang.
c) Nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Tính tổng $P(x)+Q(x)$ bằng cách thực hiện phép tính trong từng nhóm.
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến. (Ở cả 2 đa thức đã cho thì số mũ lớn nhất là 2 rồi đến 1 và 0 ).
b) Viết tổng hai đa thức theo hàng ngang.
c) Nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Thực hiện phép tính sau khi đã nhóm.
a) $P(x)=-2 x^2+1+3 x=-2 x^2+3 x+1$
$Q(x)=-5 x+3 x^2+4=3 x^2-5 x+4$
b) $P(x)+Q(x)=(-2 x^2+3 x+1)+(3 x^2-5 x+4)$
$P(x)+Q(x)=(-2 x^2+3 x+1)+(3 x^2-5 x+4)$
c) $=-2 x^2+3 x+1+3 x^2-5 x+4=(-2 x^2+3 x^2)+(3 x-5 x)+(1+4)$
$P(x)+Q(x)=(-2 x^2+3 x^2)+(3 x-5 x)+(1+4)$
d) $=(-2+3) x^2+(3-5) x+(1+4)=x^2-2 x+5$
Hoạt động 4 trang 57
b) Nêu quy tắc trừ hai đơn thức có cùng số mũ của biến.
a) Để thực hiện phép trừ trong các phép tính, ta giữ nguyên biến và trừ các hệ số cùng biến cho nhau.
b) Rút ra quy tắc trừ hai đơn thức có cùng số mũ của biến từ cách thực hiện phần $\mathrm{a}$.
a) $2 x^2-6 x^2=(2-6) x^2=-4 x^2$
$a x^k-b x^k=(a-b) x^k$
b) Muốn trừ hai đơn thức có cùng số mũ của biến, ta giữ nguyên biến và tính hiệu của các hệ số có trong đơn thức.
Hoạt động 5 trang 57
$P(x)=4 x^2+1+3 x$ và $Q(x)=5 x+2 x^2+3$
a) Sắp xếp các đa thức $P(x), Q(x)$ theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của $P(x)$ và $Q(x)$ cho ? ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
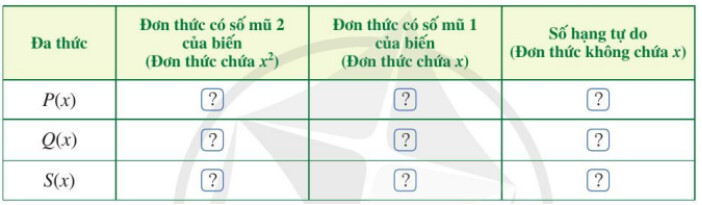
c) Dựa vào kết quả trừ hai đơn thức theo từng cột, xác định đơn thức $S(x)$.
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Quan sát bảng để đưa ra các đơn thức thích hợp phù hợp với biến có số mũ tương ứng.
c) Xác định đơn thức $S(x)$ dựa vào kết quả phần b).
a) $P(x)=4 x^2+1+3 x=4 x^2+3 x+1$
$Q(x)=5 x+2 x^2+3=2 x^2+5 x+3$
b)
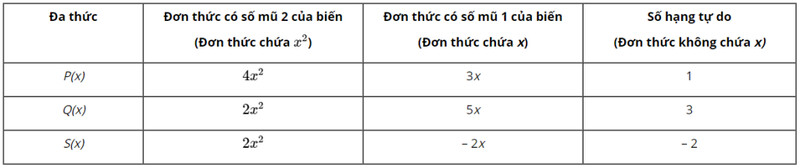
c) Vậy $S(x)=2 x^2-2 x-2$
Hoạt động 6 trang 58
$P(x)=-3 x^2+2+7 x$ và $Q(x)=-4 x+5 x^2+1$
a) Sắp xếp các đa thức $P(x)$ và $Q(x)$ theo số mũ giảm dần của biến.
b) Viết hiệu $P(x)-Q(x)$ theo hàng ngang, trong đó đa thức $Q(x)$ được đặt trong dấu ngoặc.
c) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức $Q(x)$, nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Tính hiệu $P(x)-Q(x)$ bằng cách thực hiện phép tính trong từng nhóm.
a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến. (ở cả 2 đa thức đã cho thì số mũ lớn nhất là 2 rồi đến 1 và 0 ).
b) Viết hiệu hai đa thức theo hàng ngang.
c) Nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Thực hiện phép tính sau khi đã nhóm.
a) $P(x)=-3 x^2+2+7 x=-3 x^2+7 x+2$
$Q(x)=-4 x+5 x^2+1=5 x^2-4 x+1$
b) $P(x)-Q(x)=-3 x^2+7 x+2-(5 x^2-4 x+1)$
$P(x)-Q(x)=-3 x^2+7 x+2-(5 x^2-4 x+1)$
c) $=-3 x^2+7 x+2-5 x^2+4 x-1$
$=(-3 x^2-5 x^2)+(7 x+4 x)+(2-1)$
d) $P(x)-Q(x)=(-3 x^2-5 x^2)+(7 x+4 x)+(2-1)=-8 x^2+11 x+1$
Luyện tập vận dụng 1 trang 55
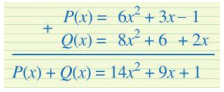
Xem lại cách thức cộng hai đơn thức theo hàng dọc:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
– Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
Và xem lại Ví dụ 2.
Cách làm của bạn Dũng chưa đúng.
Lí do:
+ Vì các đơn thức 3x và 6 không có cùng số mũ của biến nên chúng không được viết ở cùng cột.
+ Vì các đơn thức – 1 và 2x không có cùng số mũ của biến nên chúng không được viết ở cùng cột.
Các đơn thức 3x và 2x sẽ được viết cùng cột (cùng có số mũ của biến là 1); các đơn thức 6 và – 1 sẽ được viết cùng cột (cùng số mũ của biến là 0).
Cách viết đúng là:
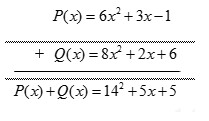
Luyện tập vận dụng 2 trang 56
$P(x)=2 x^3+\frac{3}{2} x^2+5 x-2$
$Q(x)=-8 x^3+4 x^2+6+3 x$
Nhớ lại cách thức cộng hai đa thức theo cột dọc và theo hàng ngang:
Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
– Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Viết tổng hai đơn thức theo hàng ngang;
– hóm các đơn thức có cùng số mũ của biến với nhau;
– Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
Theo cột dọc:
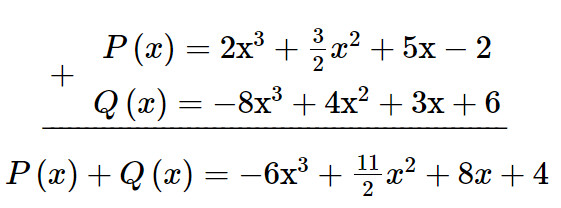
Theo hàng ngang:
$P(x)+Q(x)=2 x^3+\frac{3}{2} x^2+5 x-2+(-8) x^3+4 x^2+3 x+6$
$=(2-8) x^3+(\frac{3}{2}+4) x^2+(5+3) x+(-2+6)$
$=-6 x^3+\frac{11}{2} x^2+8 x+4$
Luyện tập vận dụng 3 trang 58
$P(x)=2 x^2-5 x-\frac{1}{3}$ và $Q(x)=-6 x^4+5 x^2+\frac{2}{3}+3 x$
Tính hiệu $P(x)-Q(x)$
Xem lại cách thức trừ hai đa thức theo cột dọc:
Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức $P(x)$ ở trên và đơn thức của $Q(x)$ ở dưới;
– Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
$P(x) – Q(x)$
$= (2x^2 – 5x -\frac{1}{3}) – (-6x^4 + 5x^2 + \frac{2}{3} + 3x)$
$= 2x^2 – 5x – \frac{1}{3} + 6x^4 – 5x^2 – \frac{2}{3} – 3x$
$= 6x^4 + (2x^2 – 5x^2) + (-5x – 3x) + (−\frac{1}{3}−\frac{2}{3})$
$= 6x^4 – 3x^2 – 8x – 1$
Vậy $P(x) – Q(x) = 6x^4 – 3x^2 – 8x – 1$
Luyện tập vận dụng 4 trang 59
$P(x)=6 x^3+8 x^2+5 x-2$
$Q(x)=-9 x^3+6 x^2+3+2 x$
Nhớ lại cách thức trừ hai đa thức theo cột dọc và theo hàng ngang:
Để trừ đa thức $P(x)$ cho đa thức $Q(x)$ (theo cột dọc), ta có thể làm như sau:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức $P(x)$ ở trên và đơn thức của $Q(x)$ ở dưới;
– Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Để trừ đa thức $P(x)$ cho đa thức $Q(x)$ (theo hàng ngang), ta có thể làm như sau:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Viết hiệu $P(x)-Q(x)$ theo hàng ngang, trong đó đa thức $Q(x)$ được đặt trong dấu ngoặc;
– Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức $Q(x)$, nhóm các đơn thức có cùng số mũ của biến với nhau;
Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Theo hàng dọc:
$P(x) = 6x^3 + 8x^2 + 5x – 2$
-$Q(x) = – (-9x^3 + 6x^2 + 3 + 2x)$
$=15x^3 + 2x^2 + 3x – 5$
Theo hàng ngang:
$P(x)-Q(x)=6 x^3+8 x^2+5 x-2-(-9 x^3+6 x^2+2 x+3)$
$=6 x^3+8 x^2+5 x-2+9 x^3-6 x^2-2 x-3$
$=(6+9) x^3+(8-6) x^2+(5-2) x+(-2-3)$
$=15 x^3+2 x^2+3 x-5$
Giải bài tập SGK Bài 3 Chương 6 Toán 7 Cánh diều tập 2
Sau khi đã tìm hiểu phần nội dung của bài học, cùng ôn lại những kiến thức đã học qua phần giải đáp chi tiết các bài tập trong SGK Toán 7 Cánh diều tập 2 trang 59 dưới đây nhé.
Bài tập 1 trang 59
$R(x)=-8 x^4+6 x^3+2 x^2-5 x+1$ và $S(x)=x^4-8 x^3+2 x+3$.
Tính:
a) $R(x)+S(x)$;
b) $R(x)-S(x)$.
Xem lại cách thức cộng và trừ hai đa thức:
Cộng hai đa thức:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– Viết tổng hai đơn thức theo hàng ngang;
– Nhóm các đơn thức có cùng số mũ của biến với nhau;
– Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
Trừ hai đa thức:
– Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
– V Viết hiệu $P(x)-Q(x)$ theo hàng ngang, trong đó đa thức $Q(x)$ được đặt trong dấu ngoặc;
– Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức $Q(x)$, nhóm các đơn thức có cùng số mũ của biến với nhau;
Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
a) $R(x)+S(x)=-8 x^4+6 x^3+2 x^2-5 x+1+x^4-8 x^3+2 x+3$
$=(-8+1) x^4+(6-8) x^3+2 x^2+(-5+2) x+(1+3)$
$=-7 x^4-2 x^3+2 x-3 x+4$
b) $R(x)-S(x)=-8 x^4+6 x^3+2 x^2-5 x+1-(x^4-8 x^3+2 x+3)$
$=-8 x^4+6 x^3+2 x^2-5 x+1-x^4+8 x^3-2 x-3$
$=(-8-1) x^4+(6+8) x^3+2 x^2+(-5-2) x+(1-3)$
$=-9 x^4+14 x^3+2 x-7 x-2$
Bài tập 2 trang 59
$A(x)=-8 x^5+6 x^4+2 x^2-5 x+1$ và $B(x)=8 x^5+8 x^3+2 x-3$
Muốn xác định bậc của hai đa thức là tổng và hiệu của 2 đa thức khác, ta phải tính tổng và hiệu của 2 đa thức đó. Và bậc của đa thức là số mũ cao nhất của biến có trong đa thức.
Tổng 2 đa thức:
$A(x)+B(x)=-8 x^5+6 x^4+2 x^2-5 x+1+8 x^5+8 x^3+2 x-3$
$=(-8+8) x^5+6 x^4+8 x^3+2 x^2+(-5+2) x+(1-3)$
$=6 x^4+8 x^3+2 x^2-3 x-2$
Vậy bậc của hai đa thức là tổng là: 4
Hiệu 2 đa thức:
$A(x)-B(x)=-8 x^5+6 x^4+2 x^2-5 x+1-(8 x^5+8 x^3+2 x-3)$
$=-8 x^5+6 x^4+2 x^2-5 x+1-8 x^5-8 x^3-2 x+3$
$=(-8-8) x^5+6 x^4-8 x^3+2 x^2+(-5-2) x+(1+3)$
$=-16 x^5+6 x^4-8 x^3+2 x^2-7 x+4$
Vậy bậc của hai đa thức là hiệu là: 5
Bài tập 3 trang 59
a) Ở ngân hàng thứ hai?
b) Ở cả hai ngân hàng?
a) Muốn tính sau kì hạn 1 năm, bác Ngọc có bao nhiêu tiền cả gốc lẫn lãi ở ngân hàng thứ 2. Ta cần tính số tiền bác Ngọc lãi được sau kì hạn 1 năm. (Bằng số tiền gốc nhân với lãi suất chia 100).
b) Muốn tính sau kì hạn 1 năm, bác Ngọc có bao nhiêu tiền cả gốc lẫn lãi ở cả 2 ngân hàng. Ta cần tính số tiền bác Ngọc lãi được sau kì hạn 1 năm ở ngân hàng thứ nhất (bằng số tiền gốc nhân với lãi suất chia 100) rồi cộng với số tiền ở ngân hàng thứ 2.
a) Số tiền lãi bác Ngọc có được sau kì hạn 1 năm ở ngân hàng thứ hai là:
$\frac{80 .(x+1,5)}{100}=0,8 .(x+1,5)=0,8 x+1,2$ (triệu đồng)
Vậy sau kì hạn 1 năm, số tiền bác Ngọc có được cả gốc lẫn lãi ở ngân hàng thứ hai là:
$80+(0,8 x+1,2)=0,8 x+81,2$ (triệu đồng)
b) Số tiền lãi bác Ngọc có được sau kì hạn 1 năm ở ngân hàng thứ nhất là:
$\frac{90 . x}{100}=0,9 . x$ (triệu đồng)
Vậy sau kì hạn 1 năm, số tiền bác Ngọc có được cả gốc lẫn lãi ở ngân hàng thứ nhất là:
$90+0,9 x$ (triệu đồng)
Vậy sau kì hạn 1 năm, số tiền bác Ngọc có được cả gốc lẫn lãi ở cả hai ngân hàng là:
$90+0,9 x+0,8 x+81,2=(0,9+0,8) x+(90+81,2)=1,7 x+171,2$ (triệu đồng)
Bài tập 4 trang 59
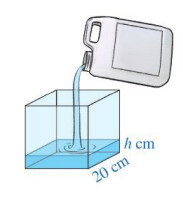
Để tính được thể tích nước còn lại trong can, ta tính thể tích của chiếc bể đến độ cao h. (Đồng nghĩa với việc tính thể tích hình hộp chữ nhật, cạnh bằng 20 và chiều cao bằng h). Rồi lấy thể tích của nước trong can ban đầu trừ đi thể tích của chiếc bể đến độ cao h.
Chú ý: Đơn vị là dm
Đổi $20 \mathrm{~cm}=2 \mathrm{dm}$; $\mathrm{h} \mathrm{~cm}=\frac{h}{10} \mathrm{dm}$.
Thể tích của chiếc bể tính đến độ cao $h$ là: $2.2 . \frac{h}{10}=0,4 . h(d m^3)=0,4 . h$ (lít)
Vậy khi mực nước trong bể cao $h(\mathrm{~cm})$ thì thể tích nước trong can còn lại là:
$10-0,4 . h$ (lít)
Bài tập 5 trang 59
Muốn kiểm tra xem hai bạn đúng hay sai, ta có thể lấy những ví dụ hoặc xem xét hệ số đi cùng biến có số mũ là bốn.
* Giả sử, cho hai đa thức biết:
– Trong đa thức thứ nhất: hệ số $a$ của đơn thức $a x^4$.
– Trong đa thức thứ hai: hệ số $-a$ của đơn thức $-a x^4$.
Như vậy, bậc của tổng của hai đa thức sẽ là bậc 3 . (Vì khi cộng hai đa thức với nhau, ta có $a+(-a)=0$ nên biến với số mũ là 4 sẽ không còn).
Vậy bạn Minh nói như vậy là không đúng.
* Giả sử, cho hai đa thức biết:
– Trong đa thức thứ nhất: hệ số $a$ của đơn thức $a x^4$.
– Trong đa thức thứ hai: hệ số $a$ của đơn thức $a x^4$.
Như vậy, bậc của hiệu của hai đa thức sẽ là bậc 3. (Vì khi trừ hai đa thức với nhau, ta có $a-a=0$ nên biến với số mũ là 4 sẽ không còn).
Vậy bạn Quân nói như vậy là không đúng.
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Bài 3 Chương VI Biểu thức đại số trang 54, 55, 56, 57, 58, 59 sách Toán 7 Cánh diều tập 2. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn học tốt!





