Giải SGK bài Hai Tam giác bằng nhau trang 78, 79 Toán 7 Cánh Diều tập 2
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, hoạt động vận dụng luyện tập cũng như bài tập cuối SGK trong bài Hai Tam giác bằng nhau trang 78, 79 Toán 7 Cánh Diều tập 2. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK bài Hai Tam giác bằng nhau trang 78 79 Toán 7 Cánh Diều
Những lời giải dưới đây sẽ giúp bạn đi tìm đáp án cho các hoạt động khởi động, luyện tạp và vận dụng ở các trang 78, 79 Toán 7 Cánh Diều trong bài Hai Tam giác bằng nhau một cách nhanh chóng và dễ hiểu. Cùng theo dõi ngay nhé!
Khởi động trang 78

Khi hai tam giác có thể chồng khít lên nhau thì các cạnh và các góc tương ứng liên hệ với nhau như thế nào?
Học sinh có thể cụ thể hóa dây chuyền sản xuất đó bằng cách cắt các hình tam giác giống nhau rồi chồng chúng lên nhau.
Khi hai tam giác có thể trồng khít lên nhau thì các cạnh tương ứng của hai tam giác bằng nhau và các góc tương ứng của hai tam giác bằng nhau.
Hoạt động 1 trang 78
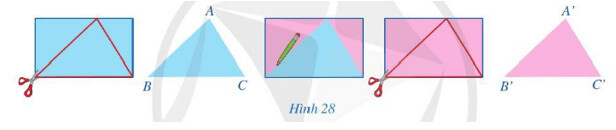
Sau khi đặt tam giác $A B C$ chồng khít lên tam giác $A^{\prime} B^{\prime} C^{\prime}$, hãy so sánh:
a) Các cạnh tương ứng: $A B$ và $A^{\prime} B^{\prime} ; B C$ và $B^{\prime} C^{\prime} ; ~ C A$ và $C^{\prime} A^{\prime} ;$
b) Các góc tương ứng: $\widehat{A}$ và $\widehat{A^{\prime}} ; \widehat{B}$ và $\widehat{B^{\prime}}, \widehat{C}$ và $\widehat{C^{\prime}}$.
Sau khi đặt tam giác $A B C$ chồng khít lên tam giác $A^{\prime} B^{\prime} C^{\prime}$ ta thấy:
a) $A B=A^{\prime} B^{\prime} ; B C=B^{\prime} C^{\prime} ; C A=C^{\prime} A^{\prime}$.
b) $\widehat{A}=\widehat{A^{\prime}} ; \widehat{B}=\widehat{B^{\prime}} ; \widehat{C}=\widehat{C^{\prime}}$
Hoạt động 2 trang 79
a) So sánh:
– Các cặp cạnh: $A B$ và $A^{\prime} B^{\prime}, B C$ và $B^{\prime} C^{\prime}, C A$ và $C^{\prime} A^{\prime}$.
– Các cặp góc: $A$ và $A^{\prime}, B$ và $B^{\prime}, C$ và $C^{\prime}$.
b) Hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có bằng nhau hay không?
c) Cắt mảnh giấy hình tam giác $A B C$ và mảnh giất hình tam giác $A^{\prime} B^{\prime} C^{\prime}$, hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?
a) Học sinh quan sát Hình 30 để so sánh các cặp cạnh và cặp góc.
b) Hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có bằng nhau hay không thì ta dựa vào mối liên hệ giữa các cặp cạnh và các cặp góc tương ứng của hai tam giác.
c) Học sinh tự thực hành cắt mảnh giấy để đưa ra kết luận.
a)
$A B=A^{\prime} B^{\prime}, B C=B^{\prime} C^{\prime}, C A=C^{\prime} A^{\prime}$
A=A^{\prime} ; B=B^{\prime}, C=C^{\prime}
b) Hai tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có bằng nhau vì chúng có các cặp cạnh và cặp góc tương ứng bằng nhau.
c) Hai hình tam giác $A B C$ và $A^{\prime} B^{\prime} C^{\prime}$ có thể đặt chồng khít lên nhau.
Luyện tập vận dụng trang 79
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.
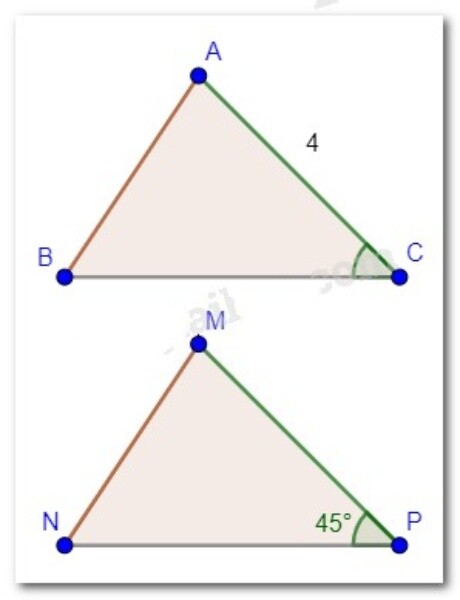
Do $\triangle \mathrm{ABC}=\triangle \mathrm{MNP}$ nên $\mathrm{AC}=\mathrm{MP}(2$ cạnh tương ứng) và $\widehat{A C B}=\widehat{M P N}$ (2 góc tương ứng).
Vậy MP $=4 \mathrm{~cm}$ và $\widehat{A C B}=45^{\circ}$.
Giải bài tập SGK bài Hai Tam giác bằng nhau trang 79 Toán 7 Cánh Diều
Để củng cố lại những kiến thức đã học, các bạn hãy cùng ôn tập qua phần giải đáp chi tiết các bài tập trong SGK bài Hai Tam giác bằng nhau trang 79 sách Toán 7 Cánh diều dưới đây nhé!
Bài 1 trang 79
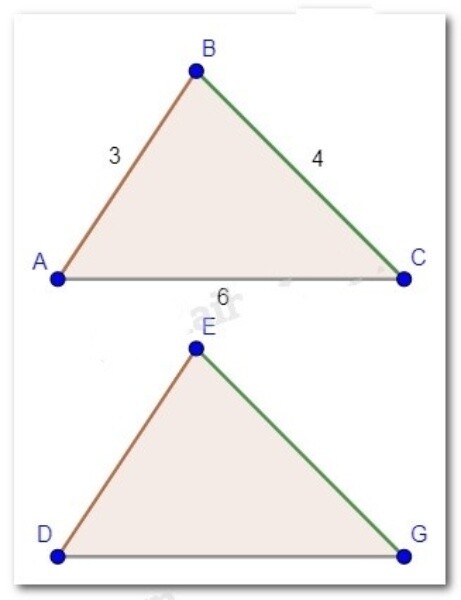
\Delta A B C=\triangle D E G \text { nên } A B=D E, B C=E G, C A=G D \text {. }
Vậy độ dài các cạnh của tam giác $D E G$ lần lượt là:
D E=3 \mathrm{~cm}, E G=4 \mathrm{~cm}, G D=6 \mathrm{~cm}
Bài 2 trang 79
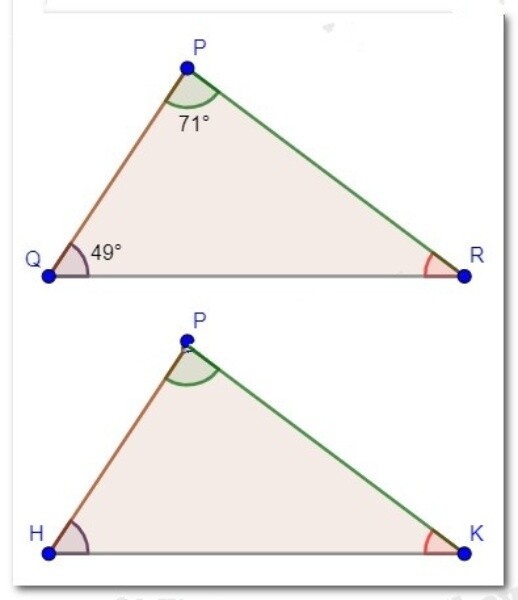
Xét tam giác PQR có: $\widehat{P}+\widehat{Q}+\widehat{R}=180^{\circ}$.
Suy ra
\widehat{R}=180^{\circ}-\widehat{P}-\widehat{Q}=180^{\circ}-71^{\circ}-49^{\circ}=60^{\circ} \text {. }
Do $\triangle \mathrm{PQR}=\Delta \mathrm{HHK}$ nên $\widehat{R}=\widehat{K}$ (2 góc tương ứng).
Do đó $\widehat{K}=60^{\circ}$.
Bài 3 trang 79
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.
Tổng ba góc trong một tam giác bằng 180°.
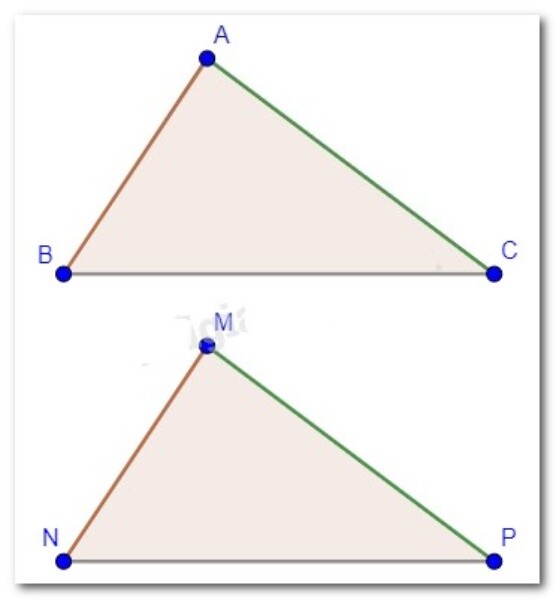
Ta có: $\triangle A B C=\triangle M N P$ nên
\widehat{A}=\widehat{M}, \widehat{B}=\widehat{N}, \widehat{C}=\widehat{P}
Mà $\widehat{A}+\widehat{N}=125^{\circ}$ hay $\widehat{M}+\widehat{N}=125^{\circ}$. Tổng ba góc trong một tam giác bằng $180^{\circ}$.
Trong tam giác MNP.
\widehat{M}+\widehat{N}+\widehat{P}=180^{\circ} \\ 125^{\circ}+\widehat{P}=180^{\circ} \\ \rightarrow \widehat{P}=180^{\circ}-125^{\circ}=55^{\circ}
Vậy số đo góc $P$ là $55^{\circ}$.
Bài 4 trang 79
a) $M$ là trung điểm của đoạn thẳng $B C$;
b) Tia $A M$ là tia phân giác của góc $B A C$ và $A M \perp B C$.4.
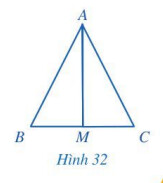
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng và các góc tương ứng bằng nhau.
a) Muốn chứng minh $M$ là trung điểm của đoạn thẳng $B C$, ta chứng minh $M B=M C$.
b) Muốn chứng minh tia $A M$ là phân giác của góc $B A C$ ta chứng minh góc $B A M=$ góc $C A M$.
Trong một tam giác, một đường thẳng vừa là trung tuyến vừa là phân giác thì đường thẳng đó vuông góc với đáy tương ứng. Hoặc ta có thể chứng minh góc được tạo bởi hai đường thẳng đó có số đo góc là $90^{\circ}$.
a) Ta có: $\triangle A M B=\Delta A M C$ nên $A B=A C, M B=M C$ nên $M$ là trung điểm của đoạn thẳng $B C$.
b) Ta có: $\triangle A M B=\Delta A M C$ nên
$\widehat{A M B}=\widehat{A M C}, \widehat{M A B}=\widehat{M A C}, \widehat{M B A}=\widehat{M C A}$.
Vậy tia $A M$ là tia phân giác của góc $B A C$ vì
$\widehat{M A B}=\widehat{M A C}$
Ta thấy: $\widehat{A M B}=\widehat{A M C}$ mà ba điểm $B, M, C$ thẳng hàng nên $\widehat{B M C}=180^{\circ}$.
$\Rightarrow \widehat{A M B}=\widehat{A M C}=\frac{1}{2} .\widehat{B M C}=\frac{1}{2} . 180^{\circ}=90^{\circ}$.
Vậy $A M \perp B C$
Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi về Giải SGK bài Hai Tam giác bằng nhau trang 78, 79 Toán 7 Cánh Diều tập 2. Hi vọng các bạn có một buổi học thật thú vị và tiếp thu được nhiều kiến thức bổ ích. Chúc các bạn học tốt!





