Giải SGK Bài 3 trang 100, 101, 102, 103, 104 chương IV Toán 7 Cánh diều tập 1
Trong bài này, HocThatGioi sẽ cùng bạn giải quyết toàn bộ các câu hỏi khởi động, hoạt động vận dụng luyện tập cũng như bài tập cuối SGK trong bài Hai đường thẳng song song trang 100, 101, 102, 103, 104 Toán 7 Cánh Diều tập 1. Hy vọng các bạn có thể hiểu được trọn vẹn bài học sau khi xem hết các phương pháp giải và lời giải cực chi tiết mà HocThatGioi trình bày ở dưới.
Trả lời câu hỏi SGK Bài 3 Chương 4 trang 100, 101, 102, 103 Toán 7 Cánh Diều tập 1
Khởi động bài học với những câu hỏi hoạt động và luyện tập vận dụng sẽ giúp bạn dễ dàng tiếp thu kiến thức về bài học Hai đường thẳng song song.
Câu hỏi khởi động trang 100
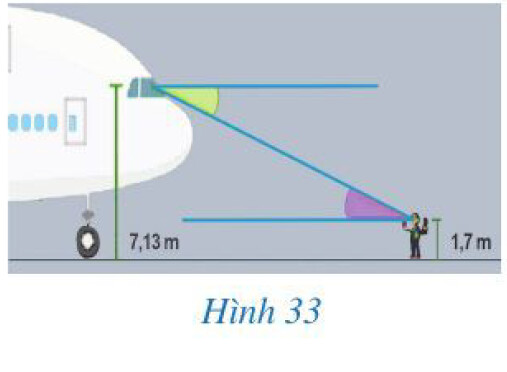
Theo em dự đoán, hai góc đó có bằng nhau hay không?
Ước lượng số đo 2 góc
Theo em dự đoán, hai góc đó có bằng nhau
Hoạt động 2 trang 101
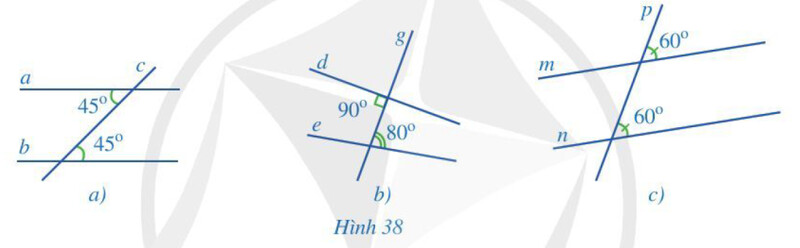
2 đường thẳng song song là hai đường thẳng không có điểm chung
Hình 38a: a và b song song
Hình 38b: không có 2 đường thẳng nào song song
Hình 38c: m và n song song
Hoạt động 3 trang 102
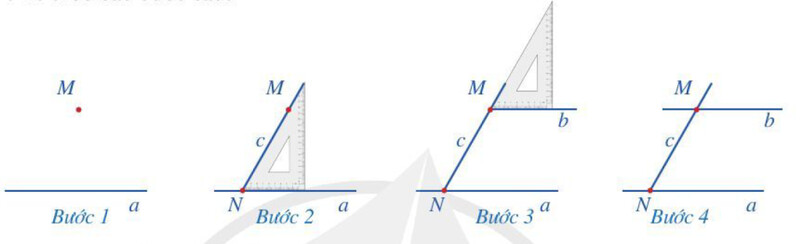
b) Giải thích vì sao đường thẳng b song song với đường thẳng a
Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
b) Đường thẳng b song song với đường thẳng a vì đường thẳng c cắt 2 đường thẳng a và b tạo ra một cặp góc đồng vị bằng nhau
Luyện tập vận dụng trang 103
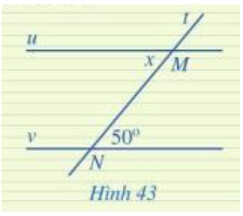
Sử dụng tính chất: Đường thẳng c cắt 2 đường thẳng song song, tạo thành 1 cặp góc so le trong bằng nhau.
Vì u // v nên x = 50^o ( 2 góc so le trong)
Giải bài tập SGK Bài 3 Chương 4 trang 104 Toán 7 Cánh Diều tập 1
Sau khi đã tìm hiểu phần nội dung của bài học, cùng ôn lại những kiến thức đã học qua phần giải đáp chi tiết các bài tập trong SGK Toán 7 Cánh diều tập 1 trang 104 dưới đây nhé.
Bài tập 1 trang 104
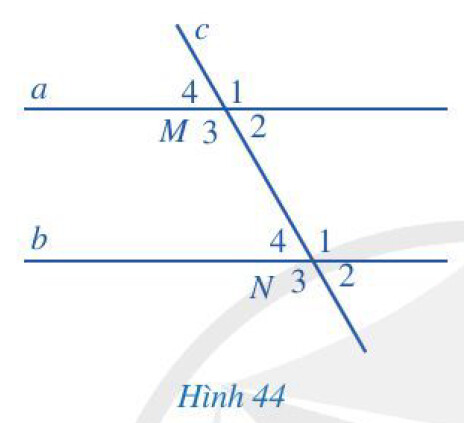
a) So sánh $\widehat{M_1}$ và $\widehat{N_3} ; \widehat{M_4}$ và $\widehat{N_2}$ ( mỗi cặp góc $\mathrm{M}_1$ và $\mathrm{N}_3, \mathrm{M}_4$ và $\mathrm{N}_2$ gọi là một cặp góc so le ngoài)
b) Tính: $\widehat{M_2}+\widehat{N_1}$ và $\widehat{M_3}+\widehat{N_4}$ ( mỗi cặp góc $\mathrm{M}_2$ và $\mathrm{N}_1, \mathrm{M}_3$ và $\mathrm{N}_4$ gọi là một cặp góc trong cùng phía)
+ 1 đường thẳng cắt 2 đường thẳng song song tạo ra các cặp góc so le trong bằng nhau, đồng vị bằng nhau.
+2 góc đối đỉnh thì bằng nhau.
+ 2 góc kề bù có tổng số đo bằng $180^{\circ}$
a) Vì $a // b$ nên $\widehat{M_1}=\widehat{N_1} ; \widehat{M_4}=\widehat{N_4}$ ( 2 góc đồng vị) mà $\widehat{N_3}=\widehat{N_1}$; $\widehat{N_4}=\widehat{N_2}$ ( 2 góc đối đỉnh) nên $\widehat{M_1}=\widehat{N_3} ; \widehat{M_4}=\widehat{N_2}$
b) Vì $a // b$ nên $\widehat{M_2}=\widehat{N_2} ; \widehat{M_3}=\widehat{N_3}$ ( 2 góc đồng vị), mà $\widehat{N_1}+\widehat{N_2}=180^{\circ} ; \widehat{N_3}+\widehat{N_4}=180^{\circ}$ ( 2 góc kề bù) nên $\widehat{M_2}+\widehat{N_1}=$ $180^{\circ} ; \widehat{M_3}+\widehat{N_4}=180^{\circ}$
Chú ý:
Nếu đường thẳng $\mathrm{c}$ cắt cả hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau
+ Hai góc trong cùng phía có tổng số đo bằng $180^{\circ}$
Bài tập 2 trang 104
a) Vì sao hai đường thẳng $a$ và $b$ song song với nhau?
b) Tính số đo góc $BCD$.
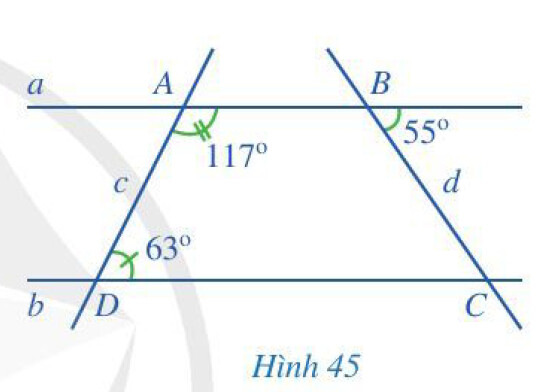
+ Sử dụng tính chất: Hai góc kề bù có tổng số đo bằng 180 độ
+ Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong bằng nhau hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ Sử dụng tính chất: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
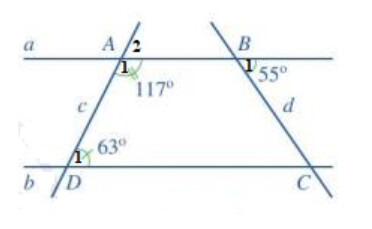
a) Vì $\widehat{A_1}+\widehat{A_2}=180^{\circ} \quad(2$ góc kề bù) nên $117^{\circ}+\widehat{A_2}=180^{\circ} \Rightarrow \widehat{A_2}=180^{\circ}-117^{\circ}=63^{\circ}$
vì $\widehat{A_2}=\widehat{D_1}$ ( cùng bằng 63 độ)
Mà 2 góc này ở vị trí đồng vị
$\Rightarrow$ $a // b$ (Dấu hiệu nhận biết hai đường thẳng song song) ( đpcm)
b) Vì $a // b$ nên $\widehat{B_1}=\widehat{B C D}$ ( 2 góc so le trong), mà $\widehat{B_1}=55^{\circ} \Rightarrow \widehat{B C D}=55^{\circ}$
Bài tập 3 trang 104
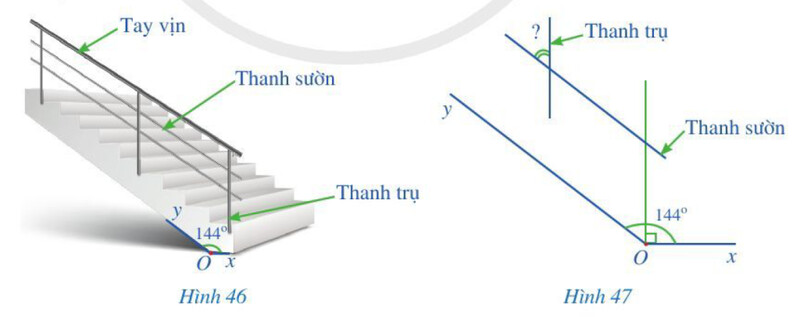
Trong Hình 46, góc $xOy$ bằng 144^o . Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ?
Sử dụng tính chất:
+ Hai góc kề bù có tổng số đo bằng 180 độ
+ Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
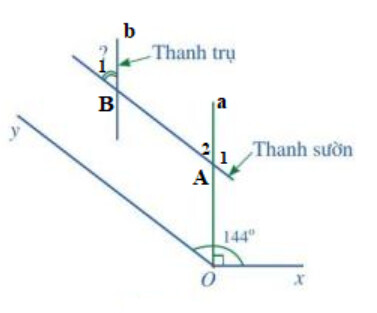
Ta có: $\widehat{x O a}+\widehat{a O y}=\widehat{x O y} \Rightarrow \widehat{a O y}=144^0-90^0=54^0$
Vì $AB // Oy$ nên $\widehat{a O y}=\widehat{A_2}$ ( 2 góc đồng vị) $\Rightarrow \widehat{A_2}=54^{\circ}$
Vì $a // b$ nên $\widehat{B_1}=\widehat{A_2}$ ( 2 góc đồng vị) $\Rightarrow \widehat{B_1}=54^{\circ}$
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Bài 3 Chương IV Góc – Đường thẳng song song trang 100, 101, 102, 103, 104 sách Toán 7 Cánh diều tập 1. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn học tốt!





