SGK Toán 7 - Cánh Diều
Giải SGK Bài tập cuối chương 7 trang 119, 120 Toán 7 Cánh diều tập 2
Ở bài viết lần này, HocThatGioi sẽ trả lời các câu hỏi ôn tập trong phần Bài tập cuối chương VII trang 119, 120 SGK Toán 7 Cánh diều tập 2. Hy vọng những lời giải chi tiết dưới đây sẽ giúp bạn hiểu và nắm rõ các kiến thức của phần ôn tập cuối chương này.
Bài tập 1 trang 119
Cho tam giác $A B C$ có: $\widehat{A}=42^{\circ}, \widehat{B}=37^{\circ}$.
a) Tính $\widehat{C}$.
b) So sánh độ dài các cạnh $A B, B C, C A$.
a) Tính $\widehat{C}$.
b) So sánh độ dài các cạnh $A B, B C, C A$.
Phương pháp giải:
a) Tổng số đo ba góc trong một tam giác bằng $180^{\circ}$.
b) Cạnh đối diện với góc lớn hơn thì có số đo độ dài lớn hơn.
a) Tổng số đo ba góc trong một tam giác bằng $180^{\circ}$.
b) Cạnh đối diện với góc lớn hơn thì có số đo độ dài lớn hơn.
Lời giải chi tiết:
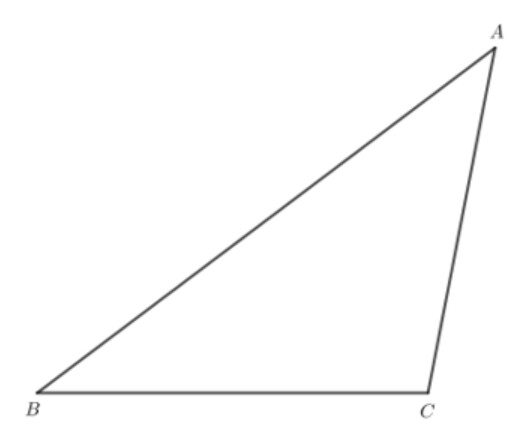
a) Trong tam giác $A B C: \widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=180^{\circ}-42^{\circ}-37^{\circ}=101^{\circ}$.
b) Trong tam giác $A B C: \widehat{B}<\widehat{A}<\widehat{C}$ nên $A C \lt B C \lt A B$. (Vì $A C$ đối diện với góc $B ; B C$ đối diện với góc $A$; $A B$ đối diện với góc $C$ ).

a) Trong tam giác $A B C: \widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=180^{\circ}-42^{\circ}-37^{\circ}=101^{\circ}$.
b) Trong tam giác $A B C: \widehat{B}<\widehat{A}<\widehat{C}$ nên $A C \lt B C \lt A B$. (Vì $A C$ đối diện với góc $B ; B C$ đối diện với góc $A$; $A B$ đối diện với góc $C$ ).
Bài tập 2 trang 119
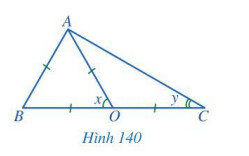
Tìm các số đo x, y trong Hình 140.

Phương pháp giải:
Tổng ba góc trong một tam giác bằng $180^{\circ}$.
Trong tam giác đều, ba góc có số đo bằng nhau và bằng $60^{\circ}$.
Tổng ba góc trong một tam giác bằng $180^{\circ}$.
Trong tam giác đều, ba góc có số đo bằng nhau và bằng $60^{\circ}$.
Lời giải chi tiết:
Tam giác $A B O$ là tam giác đều nên $\widehat{A B O}=\widehat{A O B}=\widehat{B A O}=60^{\circ}$. Vậy $x=60^{\circ}$
Ba điểm $B, O, C$ thẳng hàng nên $\widehat{B O C}=180^{\circ}$. Mà $\widehat{A O B}=60^{\circ}$ nên $\widehat{A O C}=180^{\circ}-60^{\circ}=120^{\circ}$
Xét tam giác $A O C$ có $O A=O C$. Vậy tam giác $A O C$ cân tại $O$ nên $\widehat{O A C}=\widehat{O C A}=\frac{1}{2} .\left(180^{\circ}-\widehat{A O C}\right)=\frac{1}{2} .\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$
Hay $y=30^{\circ}$
Vậy $x=60^{\circ} ; y=30^{\circ}$
Tam giác $A B O$ là tam giác đều nên $\widehat{A B O}=\widehat{A O B}=\widehat{B A O}=60^{\circ}$. Vậy $x=60^{\circ}$
Ba điểm $B, O, C$ thẳng hàng nên $\widehat{B O C}=180^{\circ}$. Mà $\widehat{A O B}=60^{\circ}$ nên $\widehat{A O C}=180^{\circ}-60^{\circ}=120^{\circ}$
Xét tam giác $A O C$ có $O A=O C$. Vậy tam giác $A O C$ cân tại $O$ nên $\widehat{O A C}=\widehat{O C A}=\frac{1}{2} .\left(180^{\circ}-\widehat{A O C}\right)=\frac{1}{2} .\left(180^{\circ}-120^{\circ}\right)=30^{\circ}$
Hay $y=30^{\circ}$
Vậy $x=60^{\circ} ; y=30^{\circ}$
Bài tập 3 trang 119
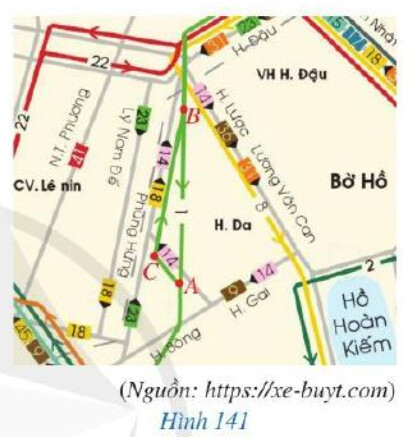
Bạn Hoa đánh dấu ba vị trí $A, B, C$ trên một phần sơ đồ xe buýt ở Hà Nội năm 2021 và xem xe buýt có thể đi như thế nào giữa hai vị trí $A$ và $B$. Đường thứ nhất đi từ $A$ đến $C$ và đi tiếp từ $C$ đến $B$, đường thứ hai đi từ $B$ đến $A$ (Hình 141). Theo em, đường nào đi dài hơn? Vì sao?
Phương pháp giải:
Trong một tam giác, tổng hai cạnh luôn lớn hơn độ dài cạnh còn lại.
Trong một tam giác, tổng hai cạnh luôn lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết:
Xét tam giác $A B C$ có: $A C+C B>A B$.
Vậy nên bạn Hoa đi đường thứ nhất đi từ $A$ đến $C$ và đi tiếp từ $C$ đến $B$ sẽ dài hơn đi đường thứ hai đi từ $B$ đến $A$.
Xét tam giác $A B C$ có: $A C+C B>A B$.
Vậy nên bạn Hoa đi đường thứ nhất đi từ $A$ đến $C$ và đi tiếp từ $C$ đến $B$ sẽ dài hơn đi đường thứ hai đi từ $B$ đến $A$.
Bài tập 4 trang 119
Cho hai tam giác $A B C$ và $M N P$ có: $A B=M N$, $B C=N P, C A=P M$. Gọi $I$ và $K$ lần lượt là trung điểm của $B C$ và $N P$. Chứng minh $A I=M K$.
Phương pháp giải:
Chứng minh $AI = MK$ bằng cách chứng hai tam giác $ABI$ và $MNK$ bằng nhau.
Chứng minh $AI = MK$ bằng cách chứng hai tam giác $ABI$ và $MNK$ bằng nhau.
Lời giải chi tiết:
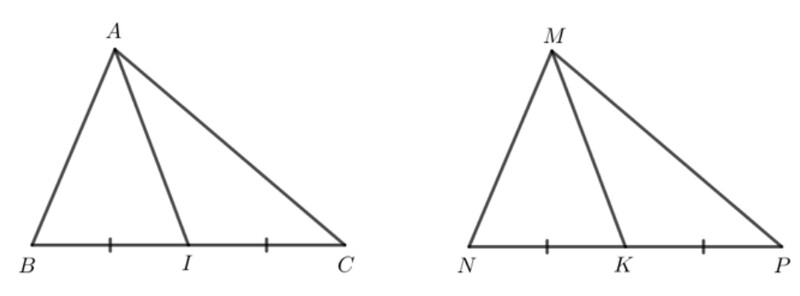
Hai tam giác $A B C$ và $M N P$ có: $A B=M N, B C=N P, C A=P M$ nên $\Delta A B C=\Delta M N P$ (c.c.c)
Suy ra: $\widehat{A B I}=\widehat{M N K}$ ( 2 góc tương ứng).
Ta có: $I, K$ lần lượt là trung điểm của $B C$ và $N P$ mà $B C=N P$, suy ra: $B I=N K$.
Xét tam giác $A B I$ và tam giác $M N K$ có:
$A B=M N ; \widehat{A B I}=\widehat{M N K} ; B I=N K$
Vậy $\Delta A B I=\Delta M N K$ (c.g.c). Suy ra: $A I=M K$ (2 cạnh tương ứng).
Vậy $A I=M K$.

Hai tam giác $A B C$ và $M N P$ có: $A B=M N, B C=N P, C A=P M$ nên $\Delta A B C=\Delta M N P$ (c.c.c)
Suy ra: $\widehat{A B I}=\widehat{M N K}$ ( 2 góc tương ứng).
Ta có: $I, K$ lần lượt là trung điểm của $B C$ và $N P$ mà $B C=N P$, suy ra: $B I=N K$.
Xét tam giác $A B I$ và tam giác $M N K$ có:
$A B=M N ; \widehat{A B I}=\widehat{M N K} ; B I=N K$
Vậy $\Delta A B I=\Delta M N K$ (c.g.c). Suy ra: $A I=M K$ (2 cạnh tương ứng).
Vậy $A I=M K$.
Bài tập 5 trang 119
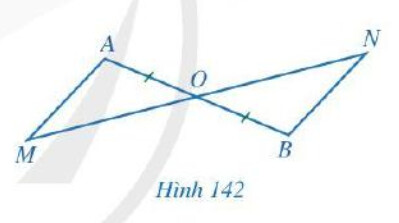
Cho Hình 142 có $O$ là trung điểm của đoạn thẳng $A B$ và $O$ nằm giữa hai điểm $M, N$. Chứng minh:
a) Nếu $O M=O N$ thì $A M / / B N$;
b) Nếu $A M / / B N$ thì $O M=O N$.
a) Nếu $O M=O N$ thì $A M / / B N$;
b) Nếu $A M / / B N$ thì $O M=O N$.

Phương pháp giải:
Chứng minh dựa vào chứng minh hai tam giác $A O M$ và $B O N$ bằng nhau.
Chứng minh dựa vào chứng minh hai tam giác $A O M$ và $B O N$ bằng nhau.
Lời giải chi tiết:
a) Xét tam giác $A O M$ và tam giác $B O N$ có:
$O A=O B$
$\widehat{A O M}=\widehat{B O N}$ (đối đỉnh);
$O M=O N$
Vậy $\triangle A O M=\triangle B O N($ c.g.c).
Suy ra: $\widehat{A M O}=\widehat{B N O}$ (2 góc tương ứng).
Mà hai góc này ở vị trí so le trong nên $A M / / B N$.
b) Ta có: $A M / / B N$ nên $\widehat{M A O}=\widehat{N B O}$ (hai góc so le trong).
Xét tam giác $A O M$ và tam giác $B O N$ có:
$\widehat{M A O}=\widehat{N B O}$
$O A=O B$
$\widehat{A O M}=\widehat{B O N}$ (đối đỉnh);
Vậy $\triangle A O M=\triangle B O N$ (g.c.g).
Suy ra: $O M=O N$ ( 2 cạnh tương ứng).
a) Xét tam giác $A O M$ và tam giác $B O N$ có:
$O A=O B$
$\widehat{A O M}=\widehat{B O N}$ (đối đỉnh);
$O M=O N$
Vậy $\triangle A O M=\triangle B O N($ c.g.c).
Suy ra: $\widehat{A M O}=\widehat{B N O}$ (2 góc tương ứng).
Mà hai góc này ở vị trí so le trong nên $A M / / B N$.
b) Ta có: $A M / / B N$ nên $\widehat{M A O}=\widehat{N B O}$ (hai góc so le trong).
Xét tam giác $A O M$ và tam giác $B O N$ có:
$\widehat{M A O}=\widehat{N B O}$
$O A=O B$
$\widehat{A O M}=\widehat{B O N}$ (đối đỉnh);
Vậy $\triangle A O M=\triangle B O N$ (g.c.g).
Suy ra: $O M=O N$ ( 2 cạnh tương ứng).
Bài tập 6 trang 119
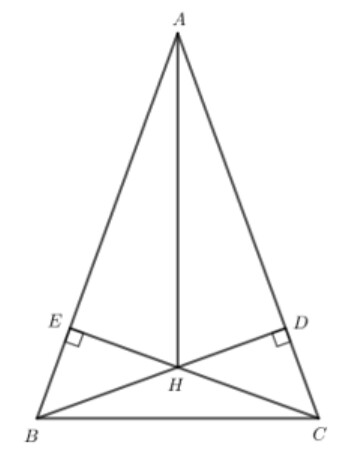
Cho tam giác $A B C$ cân tại $A$ có $\widehat{A B C}=70^{\circ}$. Hai đường cao $B D$ và $C E$ cắt nhau tại $H$
a) Tính số đo các góc còn lại của tam giác $A B C$.
b) Chứng minh $B D=C E$.
c) Chứng minh tia $A H$ là tia phân giác của góc $B A C$.
a) Tính số đo các góc còn lại của tam giác $A B C$.
b) Chứng minh $B D=C E$.
c) Chứng minh tia $A H$ là tia phân giác của góc $B A C$.
Phương pháp giải:
a) Tam giác ABC cân tại A nên số đo góc B bằng số đo góc C và tổng ba góc trong một tam giác bằng 180°.
b) Chứng minh hai tam giác vuông ADB và AEC bằng nhau.
c) Chứng minh $\widehat{BAH}=\widehat{CAH}$
a) Tam giác ABC cân tại A nên số đo góc B bằng số đo góc C và tổng ba góc trong một tam giác bằng 180°.
b) Chứng minh hai tam giác vuông ADB và AEC bằng nhau.
c) Chứng minh $\widehat{BAH}=\widehat{CAH}$
Lời giải chi tiết:
a) Tam giác $A B C$ cân tại $A$ nên: $\widehat{A B C}=\widehat{A C B}=70^{\circ}$.
Tổng ba góc trong một tam giác bằng $180^{\circ}$ nên: $\widehat{B A C}=180^{\circ}-70^{\circ}-70^{\circ}=40^{\circ}$.
b) Xét tam giác vuông $A D B$ và tam giác vuông $A E C$ có:
$A B=A C$ (tam giác $A B C$ cân);
$\widehat{A}$ chung.
Vậy $\triangle A D B=\triangle A E C$ (cạnh huyền – góc nhọn). Suy ra: $B D=C E$ ( 2 cạnh tương ứng).
c) Trong tam giác $A B C$ có $H$ là giao điểm của hai đường cao $B D$ và $C E$ nên $H$ là trực tâm trong tam giác $A B C$ hay $A F$ vuông góc với $B C$.
Xét hai tam giác vuông $A F B$ và $A F C$ có:
$A B=A C$ (tam giác $A B C$ cân);
$A F$ chung.
Vậy $\triangle A F B=\triangle A F C$ (cạnh huyền – cạnh góc vuông). Suy ra: $\widehat{F A B}=\widehat{F A C}$ ( 2 góc tương ứng) hay $\widehat{B A H}=\widehat{C A H}$.
Vậy tia $A H$ là tia phân giác của góc $B A C$.

a) Tam giác $A B C$ cân tại $A$ nên: $\widehat{A B C}=\widehat{A C B}=70^{\circ}$.
Tổng ba góc trong một tam giác bằng $180^{\circ}$ nên: $\widehat{B A C}=180^{\circ}-70^{\circ}-70^{\circ}=40^{\circ}$.
b) Xét tam giác vuông $A D B$ và tam giác vuông $A E C$ có:
$A B=A C$ (tam giác $A B C$ cân);
$\widehat{A}$ chung.
Vậy $\triangle A D B=\triangle A E C$ (cạnh huyền – góc nhọn). Suy ra: $B D=C E$ ( 2 cạnh tương ứng).
c) Trong tam giác $A B C$ có $H$ là giao điểm của hai đường cao $B D$ và $C E$ nên $H$ là trực tâm trong tam giác $A B C$ hay $A F$ vuông góc với $B C$.
Xét hai tam giác vuông $A F B$ và $A F C$ có:
$A B=A C$ (tam giác $A B C$ cân);
$A F$ chung.
Vậy $\triangle A F B=\triangle A F C$ (cạnh huyền – cạnh góc vuông). Suy ra: $\widehat{F A B}=\widehat{F A C}$ ( 2 góc tương ứng) hay $\widehat{B A H}=\widehat{C A H}$.
Vậy tia $A H$ là tia phân giác của góc $B A C$.
Bài tập 7 trang 119
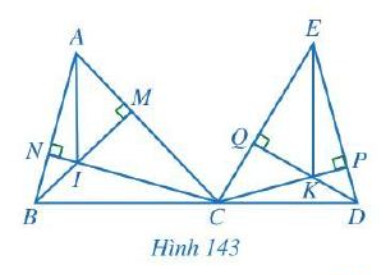
Cho hai tam giác nhọn $A B C$ và $E C D$, trong đó ba điểm $B, C, D$ thẳng hàng. Hai đường cao $B M$ và $C N$ của tam giác $A B C$ cắt nhau tại $I$, hai đường cao $C P$ và $D Q$ của tam giác $E C D$ cắt nhau tại $K$ (Hình 143). Chứng minh $A I / / E K$.

Phương pháp giải:
Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Lời giải chi tiết:
Ta có:
$I$ là giao điểm của hai đường cao $B M, C N$ trong tam giác $A B C$. Suy ra $I$ là trực tâm của tam giác $A B C$. Vậy $A I \perp B C$. (1)
$K$ là giao điểm của hai đường cao $D Q, C P$ trong tam giác $C E D$. Suy ra $K$ là trực tâm của tam giác $C E D$.
Vậy $E K \perp C D$. (2)
Mà ba điểm $B, C, D$ thẳng hàng. (3)
Từ (1), (2) và (3) suy ra: $AI / / E K$.
Ta có:
$I$ là giao điểm của hai đường cao $B M, C N$ trong tam giác $A B C$. Suy ra $I$ là trực tâm của tam giác $A B C$. Vậy $A I \perp B C$. (1)
$K$ là giao điểm của hai đường cao $D Q, C P$ trong tam giác $C E D$. Suy ra $K$ là trực tâm của tam giác $C E D$.
Vậy $E K \perp C D$. (2)
Mà ba điểm $B, C, D$ thẳng hàng. (3)
Từ (1), (2) và (3) suy ra: $AI / / E K$.
Bài tập 8 trang 120
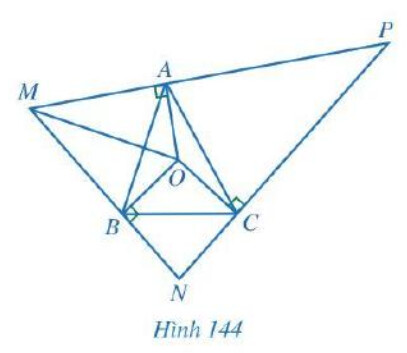
Cho tam giác $A B C$ có $O$ là giao điểm của ba đường trung trực. Qua các điểm $A, B, C$ lần lượt kẻ các đường thẳng vuông góc với $O A, O B, O C$, hai trong ba đường đó lần lượt cắt nhau tại $M, N, P$ (Hình 144). Chứng minh:
a) $\triangle O M A=\triangle O M B$ và tia $M O$ là tia phân giác của góc $N M P$;
b) $O$ là giao điểm của ba đường phân giác của tam giác $M N P$.
a) $\triangle O M A=\triangle O M B$ và tia $M O$ là tia phân giác của góc $N M P$;
b) $O$ là giao điểm của ba đường phân giác của tam giác $M N P$.

Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh dựa vào kết quả của phần a)
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh dựa vào kết quả của phần a)
Lời giải chi tiết:
a) $O$ là giao điểm của ba đường trung trực của tam giác $A B C$ nên $O$ cách đều ba đỉnh của tam giác đó hay $O A=O B=O C$. Xét hai tam giác vuông $O A M$ và $O B M$ có:
$O A=O B$
$O M$ chung.
Vậy $\triangle O A M=\triangle O B M$ (cạnh huyền – cạnh góc vuông).
Suy ra: $\widehat{O M A}=\widehat{B M O}$ (2 góc tương ứng).
Vậy $M O$ là tia phân giác của góc $B M A$ hay $M O$ là tia phân giác của góc $N M P$ (ba điểm $M, A, P$ thẳng hàng và ba điểm $M, B, N$ thẳng hàng).
b) $M O$ là tia phân giác của góc $N M P$.
Tương tự ta có:
$N O$ là tia phân giác của góc $M N P$.
$P O$ là tia phân giác của góc $M P N$.
Vậy $O$ là giao điểm của ba đường phân giác $M O, N O, P O$ của tam giác $M N P$.
a) $O$ là giao điểm của ba đường trung trực của tam giác $A B C$ nên $O$ cách đều ba đỉnh của tam giác đó hay $O A=O B=O C$. Xét hai tam giác vuông $O A M$ và $O B M$ có:
$O A=O B$
$O M$ chung.
Vậy $\triangle O A M=\triangle O B M$ (cạnh huyền – cạnh góc vuông).
Suy ra: $\widehat{O M A}=\widehat{B M O}$ (2 góc tương ứng).
Vậy $M O$ là tia phân giác của góc $B M A$ hay $M O$ là tia phân giác của góc $N M P$ (ba điểm $M, A, P$ thẳng hàng và ba điểm $M, B, N$ thẳng hàng).
b) $M O$ là tia phân giác của góc $N M P$.
Tương tự ta có:
$N O$ là tia phân giác của góc $M N P$.
$P O$ là tia phân giác của góc $M P N$.
Vậy $O$ là giao điểm của ba đường phân giác $M O, N O, P O$ của tam giác $M N P$.
Bài tập 9 trang 120
Cho tam giác $A B C$ có $G$ là trọng tâm, $H$ là trực tâm, $I$ là giao điểm của ba đường phân giác, $O$ là giao điểm của ba đường trung trực. Các điểm $A, G, H, I, O$ phân biệt. Chứng minh rằng:
a) Nếu tam giác $A B C$ cân tại $A$ thì các điểm $A, G, H, I, O$ cùng nằm trên một đường thẳng;
b) Nếu các điểm $A, H, I$ cùng nằm trên một đường thẳng thì tam giác $A B C$ cân tại $A$.
a) Nếu tam giác $A B C$ cân tại $A$ thì các điểm $A, G, H, I, O$ cùng nằm trên một đường thẳng;
b) Nếu các điểm $A, H, I$ cùng nằm trên một đường thẳng thì tam giác $A B C$ cân tại $A$.
Phương pháp giải:
a) Trong tam giác cân: đường trung tuyến tại đỉnh cân đồng thời là đường cao và đường phân giác của góc tại đỉnh đó.
b) Chứng minh tam giác $ABC$ cân tại $A$, ta chứng minh $AB$ = $AC$ hoặc góc $B$ bằng góc $C$.
a) Trong tam giác cân: đường trung tuyến tại đỉnh cân đồng thời là đường cao và đường phân giác của góc tại đỉnh đó.
b) Chứng minh tam giác $ABC$ cân tại $A$, ta chứng minh $AB$ = $AC$ hoặc góc $B$ bằng góc $C$.
Lời giải chi tiết:
a)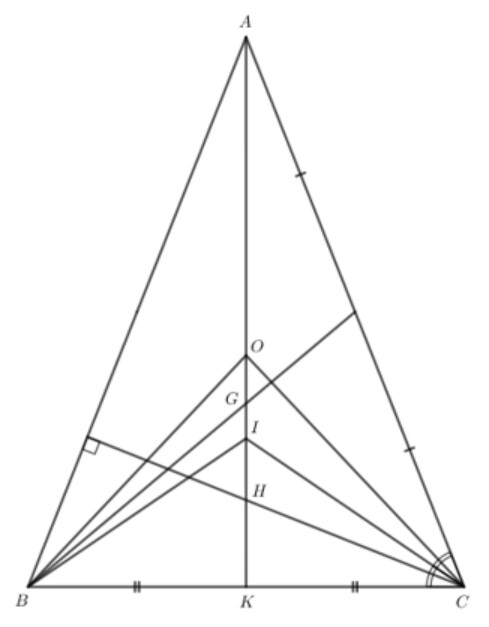
Trong tam giác $A B C$ cân tại $A$ có $A D$ là đường trung tuyến.
Xét tam giác $A B D$ và tam giác $A C D$ có:
$A B=A C$ (tam giác $A B C$ cân);
$A D$ chung;
$B D=D C(D$ là trung điểm của $B C)$.
Vậy $\triangle A B D=\triangle A C D$ (c.c.c.).
Suy ra: $\widehat{A D B}=\widehat{A D C}=90^{\circ}$ (vì ba điểm $B, D, C$ thẳng hàng);
$\widehat{B A D}=\widehat{C A D}$.
Vậy $A D$ là đường cao của tam giác và đường phân giác của góc $A$.
Suy ra: $A D$ là đường trung trực của tam giác $A B C$.
Vậy $A D$ là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác $A B C$.
Mà $G$ là trọng tâm, $H$ là trực tâm, $I$ là giao điểm của ba đường phân giác, $O$ là giao điểm của ba đường trung trực nên $A, G, H, I, O$ cùng nằm trên một đường thẳng.
Vậy nếu tam giác $A B C$ cân tại $A$ thì các điểm $A, G, H, I, O$ cùng nằm trên một đường thẳng.
b)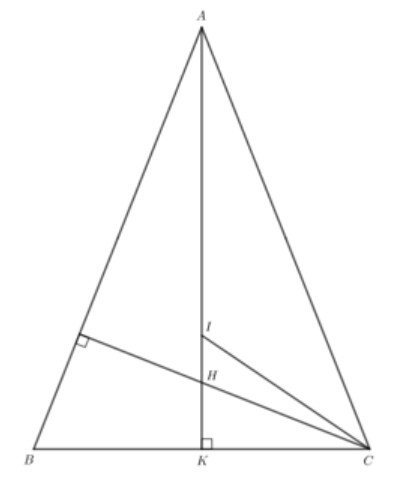
Ta có: $A D \perp B C$.
$H$ là trực tâm của tam giác $A B C$ nên $A, H, D$ thẳng hàng.
Mà $A, H, I$ thẳng hàng nên $A, H, I, K$ thẳng hàng.
Suy ra: $A D$ là tia phân giác của góc $B A C$ (Vì $AI$ là tia phân giác của góc $B A C$)
Nên $\widehat{B A D}=\widehat{C A D}$.
Xét tam giác $B A D$ và tam giác $C A D$ có:
$$\widehat{B A D}=\widehat{C A D}$$
$A D$ chung;
$\widehat{A D B}=\widehat{A D C}(A D \perp B C)$
$\triangle A B D=\triangle A C D$ (g.c.g)
Suy ra: $A B=A C$ (2 cạnh tương ứng)
Do đó, tam giác $A B C$ cân tại $A$
Vậy nếu các điểm $A, H, I$ cùng nằm trên một đường thẳng thì tam giác $A B C$ cân tại $A$.
a)

Trong tam giác $A B C$ cân tại $A$ có $A D$ là đường trung tuyến.
Xét tam giác $A B D$ và tam giác $A C D$ có:
$A B=A C$ (tam giác $A B C$ cân);
$A D$ chung;
$B D=D C(D$ là trung điểm của $B C)$.
Vậy $\triangle A B D=\triangle A C D$ (c.c.c.).
Suy ra: $\widehat{A D B}=\widehat{A D C}=90^{\circ}$ (vì ba điểm $B, D, C$ thẳng hàng);
$\widehat{B A D}=\widehat{C A D}$.
Vậy $A D$ là đường cao của tam giác và đường phân giác của góc $A$.
Suy ra: $A D$ là đường trung trực của tam giác $A B C$.
Vậy $A D$ là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác $A B C$.
Mà $G$ là trọng tâm, $H$ là trực tâm, $I$ là giao điểm của ba đường phân giác, $O$ là giao điểm của ba đường trung trực nên $A, G, H, I, O$ cùng nằm trên một đường thẳng.
Vậy nếu tam giác $A B C$ cân tại $A$ thì các điểm $A, G, H, I, O$ cùng nằm trên một đường thẳng.
b)

Ta có: $A D \perp B C$.
$H$ là trực tâm của tam giác $A B C$ nên $A, H, D$ thẳng hàng.
Mà $A, H, I$ thẳng hàng nên $A, H, I, K$ thẳng hàng.
Suy ra: $A D$ là tia phân giác của góc $B A C$ (Vì $AI$ là tia phân giác của góc $B A C$)
Nên $\widehat{B A D}=\widehat{C A D}$.
Xét tam giác $B A D$ và tam giác $C A D$ có:
$$\widehat{B A D}=\widehat{C A D}$$
$A D$ chung;
$\widehat{A D B}=\widehat{A D C}(A D \perp B C)$
$\triangle A B D=\triangle A C D$ (g.c.g)
Suy ra: $A B=A C$ (2 cạnh tương ứng)
Do đó, tam giác $A B C$ cân tại $A$
Vậy nếu các điểm $A, H, I$ cùng nằm trên một đường thẳng thì tam giác $A B C$ cân tại $A$.
Bài tập 10 trang 120
Bạn Hoa vẽ tam giác $A B C$ lên tờ giấy sau đó cắt một phần tam giác ở phía góc $A$ (Hình 145). Bạn Hoa đố bạn Hùng: Không vẽ điểm $A$, làm thế nào tìm được điểm $D$ trên đường thẳng $B C$ sao cho khoảng cách từ $D$ đến điểm $A$ là nhỏ nhất? Em hãy giúp bạn Hùng tìm cách vẽ điểm $D$ và giải thích cách làm của mình.
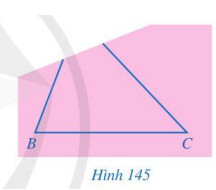

Phương pháp giải:
Vẽ giao điểm của hai đường cao từ đỉnh B, C rồi lấy giao điểm và từ giao điểm đó vẽ đường thẳng vuông góc với BC cắt BC tại D.
Vẽ giao điểm của hai đường cao từ đỉnh B, C rồi lấy giao điểm và từ giao điểm đó vẽ đường thẳng vuông góc với BC cắt BC tại D.
Lời giải chi tiết:
Trong tam giác, đường có độ dài ngắn nhất luôn là đường cao (đường vuông góc).
Vậy: khoảng cách từ $D$ đến điểm $A$ là nhỏ nhất khi $A D \perp B C$.
Bước 1: Vẽ hai đường cao hạ từ đỉnh $B$ và $C$.
Bước 2: Gọi $H$ là giao điểm của hai đường cao.
Bước 3: Vẽ đường cao hạ từ $H$ xuống $B C$. Và giao điểm của đường cao hạ từ $H$ với đoạn thẳng $B C$ là điểm $D$ ta cần tìm.
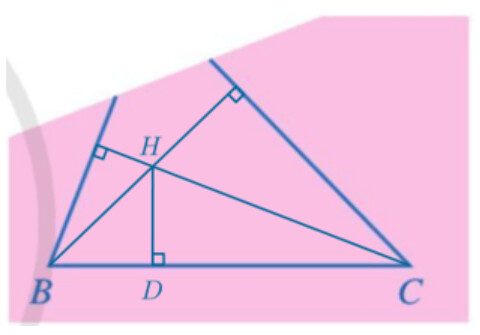
Trong tam giác, đường có độ dài ngắn nhất luôn là đường cao (đường vuông góc).
Vậy: khoảng cách từ $D$ đến điểm $A$ là nhỏ nhất khi $A D \perp B C$.
Bước 1: Vẽ hai đường cao hạ từ đỉnh $B$ và $C$.
Bước 2: Gọi $H$ là giao điểm của hai đường cao.
Bước 3: Vẽ đường cao hạ từ $H$ xuống $B C$. Và giao điểm của đường cao hạ từ $H$ với đoạn thẳng $B C$ là điểm $D$ ta cần tìm.

Bài tập 11 trang 120
Cho tam giác $A B C$ có hai đường trung tuyến $A M$ và $B N$ cắt nhau tại $G$. Khi đó
A. $A M=2 G M$.
B. $A M=2 A G$.
C. $G A=3 G M$.
D. $G A=2 G M$.
A. $A M=2 G M$.
B. $A M=2 A G$.
C. $G A=3 G M$.
D. $G A=2 G M$.
Phương pháp giải:
Khoảng cách từ đỉnh đến trọng tâm của tam giác bằng $\frac{2}{3}$ khoảng cách từ đỉnh đến trung điểm của cạnh đối diện đỉnh đó.
Khoảng cách từ đỉnh đến trọng tâm của tam giác bằng $\frac{2}{3}$ khoảng cách từ đỉnh đến trung điểm của cạnh đối diện đỉnh đó.
Lời giải chi tiết:
Đáp án D: $G A=2 G M$
Đáp án D: $G A=2 G M$
Bài tập 12 trang 120
Cho tam giác $A B C$ cân tại $A$ có $\widehat{B A C}=40^{\circ}$. Hai đường trung trực của hai cạnh $A B$, $A C$ cắt nhau tại $O$. Khi đó
A. $O A=O B=A B$.
B. $O A=O B=O C$.
C. $O B=O C=B C$.
D. $O C=O A=A C$.
A. $O A=O B=A B$.
B. $O A=O B=O C$.
C. $O B=O C=B C$.
D. $O C=O A=A C$.
Phương pháp giải:
Trong một tam giác: giao điểm của ba đường trung trực cách đều ba đỉnh của tam giác đó.
Trong một tam giác: giao điểm của ba đường trung trực cách đều ba đỉnh của tam giác đó.
Lời giải chi tiết:
Đáp án: B. $O A=O B=O C$.
Đáp án: B. $O A=O B=O C$.
Bài tập 13 trang 120
Cho tam giác $A B C$ có $B C \gt A C, I$ là giao điểm của hai đường phân giác góc $A$ và góc $B$. Khi đó
A. $\widehat{I C A}=\widehat{I C B}$
B. $\widehat{I A C}=\widehat{I B C}$.
C. $\widehat{I C A}>\widehat{I C B}$.
D. $\widehat{I A C}<\widehat{I B C}$.
A. $\widehat{I C A}=\widehat{I C B}$
B. $\widehat{I A C}=\widehat{I B C}$.
C. $\widehat{I C A}>\widehat{I C B}$.
D. $\widehat{I A C}<\widehat{I B C}$.
Phương pháp giải:
Ba đường phân giác trong tam giác cắt nhau tại một điểm.
Ba đường phân giác trong tam giác cắt nhau tại một điểm.
Lời giải chi tiết:
Ta có: $I$ là giao điểm của hai đường phân giác góc $A$ và góc $B$ nên suy ra: $C$ là đường phân giác của góc $C$.
Ta có: $I$ là giao điểm của hai đường phân giác góc $A$ và góc $B$ nên suy ra: $C$ là đường phân giác của góc $C$.
Bài tập 14 trang 120
Cho tam giác nhọn $A B C$ có $A B \lt A C$. Hai đường cao $A D$ và $C E$ cắt nhau tại $H$. Khi đó
A. $\widehat{H A B}=\widehat{H A C}$.
B. $\widehat{H A B}>\widehat{H A C}$.
C. $\widehat{H A B}=\widehat{H C B}$.
D. $\widehat{H A C}=\widehat{B A C}$.
A. $\widehat{H A B}=\widehat{H A C}$.
B. $\widehat{H A B}>\widehat{H A C}$.
C. $\widehat{H A B}=\widehat{H C B}$.
D. $\widehat{H A C}=\widehat{B A C}$.
Phương pháp giải:
Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn.
Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn.
Lời giải chi tiết:
Ta có: $A B \lt A C$ nên $\widehat{A C B} \lt \widehat{A B C}$ (góc $A C B$ đối diện với cạnh $A B$; góc $A B C$ đối diện với cạnh $A C$ )
Mà tam giác $A D B$ và tam giác $A D C$ đều vuông tại $D$.
Vì tổng hai góc nhọn trong một tam giác vuông bằng $90^{\circ}$.
Mà $\widehat{A C B} \lt \widehat{A B C}$.
Suy ra: $90^{\circ}-\widehat{A C B} \gt 90-\widehat{A B C}$ hay $\widehat{D A C} \gt \widehat{D A B}$.
Vậy $\widehat{H A C} \gt \widehat{H A B}$ hay $\widehat{H A B} \lt \widehat{H A C}$.
Suy ra: loại đáp án A, B, D.
Đáp án: C: $\widehat{H A B}=\widehat{H C B}$.
Ta có: $A B \lt A C$ nên $\widehat{A C B} \lt \widehat{A B C}$ (góc $A C B$ đối diện với cạnh $A B$; góc $A B C$ đối diện với cạnh $A C$ )
Mà tam giác $A D B$ và tam giác $A D C$ đều vuông tại $D$.
Vì tổng hai góc nhọn trong một tam giác vuông bằng $90^{\circ}$.
Mà $\widehat{A C B} \lt \widehat{A B C}$.
Suy ra: $90^{\circ}-\widehat{A C B} \gt 90-\widehat{A B C}$ hay $\widehat{D A C} \gt \widehat{D A B}$.
Vậy $\widehat{H A C} \gt \widehat{H A B}$ hay $\widehat{H A B} \lt \widehat{H A C}$.
Suy ra: loại đáp án A, B, D.
Đáp án: C: $\widehat{H A B}=\widehat{H C B}$.
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Bài tập cuối chương VII Tam giác trang 119, 120 SGK Toán 7 Cánh diều tập 2. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn ôn tập thật tốt!
Bài viết khác liên quan đến Lớp 7 – Toán – Ôn tập chương tam giác
- Giải SGK Bài tập cuối chương 8 trang 84 Toán 7 Chân trời sáng tạo tập 2
- Giải SGK Luyện tập chung trang 74 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 4 trang 87 Toán 7 Kết nối tri thức tập 1
- Giải SGK bài tập cuối chương 9 trang 84 Toán 7 Kết nối tri thức Tập 2
- Giải Luyện tập chung trang 82, 83 SGK Toán 7 Kết nối tri thức Tập 2
- Giải SGK Luyện tập chung trang 86 Toán 7 Kết nối tri thức tập 1
- Giải luyện tập chung chương 9 trang 70, 71 SGK Toán 7 Kết nối tri thức Tập 2





