SGK Toán 7 - Cánh Diều
Giải SGK Bài tập cuối chương IV Toán 7 Cánh diều tập 1
Ở bài viết lần này, HocThatGioi sẽ trả lời các câu hỏi ôn tập trong phần Bài tập cuối chương IV trang 108 SGK Toán 7 Cánh diều tập 1. Hy vọng những lời giải chi tiết dưới đây sẽ giúp bạn hiểu và nắm rõ các kiến thức của phần ôn tập cuối chương này.
Bài tập 1 trang 108
a) Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.
b) Thế nào là tia phân giác của một góc?
c) Cho một ví dụ về hai góc đồng vị, hai góc so le trong.
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau không? Hai góc so le trong có bằng nhau hay không?
e) Phát biểu tiên đề Euclid về đường thẳng song song.
b) Thế nào là tia phân giác của một góc?
c) Cho một ví dụ về hai góc đồng vị, hai góc so le trong.
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau không? Hai góc so le trong có bằng nhau hay không?
e) Phát biểu tiên đề Euclid về đường thẳng song song.
Phương pháp giải:
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
+ 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau.
+ 2 góc có tổng số đo là 180 độ là 2 góc bù nhau.
+ 2 góc kề bù nếu chúng vừa kề nhau, vừa bù nhau.
+ Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
+ 1 đường thẳng cắt 2 đường thẳng song song tạo ra các cặp góc so le trong bằng nhau, đồng vị bằng nhau.
+ Tiên đề Euclid về đường thẳng song song.
+ Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
+ 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau.
+ 2 góc có tổng số đo là 180 độ là 2 góc bù nhau.
+ 2 góc kề bù nếu chúng vừa kề nhau, vừa bù nhau.
+ Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
+ 1 đường thẳng cắt 2 đường thẳng song song tạo ra các cặp góc so le trong bằng nhau, đồng vị bằng nhau.
+ Tiên đề Euclid về đường thẳng song song.
Lời giải chi tiết:
a)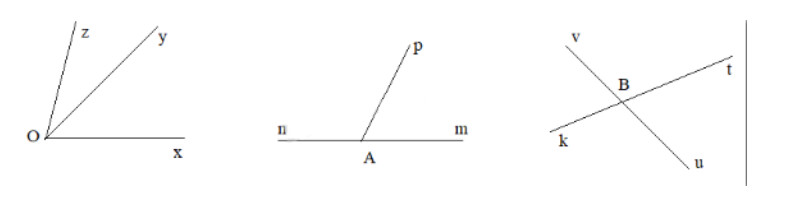
+ Ví dụ về 2 góc kề nhau: Góc $xOy$ và góc $yOz$
+ Ví dụ về 2 góc kề bù: góc $mAp$ và $pAn$
+ Ví dụ về hai góc đối đỉnh: góc $uBt$ và góc $vBk$
b) Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.
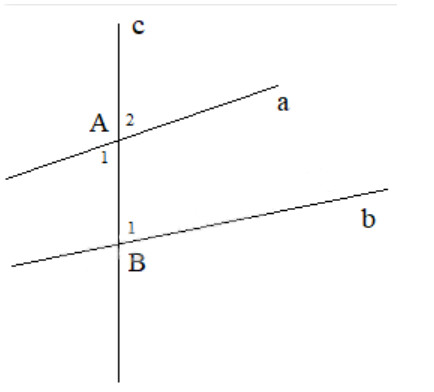
Đường thẳng c cắt hai đường thẳng a và b, tạo ra: Góc A1 và B1 là cặp góc so le trong; Góc A2 và B1 là cặp góc đồng vị
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau; hai góc so le trong bằng nhau ( Tính chất 2 đường thẳng song song)
e) Tiên đề Euclide về đường thẳng song song: Qua 1 điểm nằm ngoài đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
a)

+ Ví dụ về 2 góc kề nhau: Góc $xOy$ và góc $yOz$
+ Ví dụ về 2 góc kề bù: góc $mAp$ và $pAn$
+ Ví dụ về hai góc đối đỉnh: góc $uBt$ và góc $vBk$
b) Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

Đường thẳng c cắt hai đường thẳng a và b, tạo ra: Góc A1 và B1 là cặp góc so le trong; Góc A2 và B1 là cặp góc đồng vị
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau; hai góc so le trong bằng nhau ( Tính chất 2 đường thẳng song song)
e) Tiên đề Euclide về đường thẳng song song: Qua 1 điểm nằm ngoài đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
Bài tập 2 trang 108
a) Hai góc có tổng số đo bằng 180^ o có phải là hai góc kề bù hay không?
b) Hai góc bằng nhau và có chung đỉnh có phải là hai góc đối đỉnh hay không?
b) Hai góc bằng nhau và có chung đỉnh có phải là hai góc đối đỉnh hay không?
Phương pháp giải:
Chỉ ra một ví dụ chứng tỏ khẳng định sai
Chỉ ra một ví dụ chứng tỏ khẳng định sai
Lời giải chi tiết:
a) Hai góc có tổng số đo bằng 180^ o không phải là hai góc kề bù, vì 2 góc kề bù phải là 2 góc kề nhau và có tổng số đo bằng 180^ o , chẳng hạn:
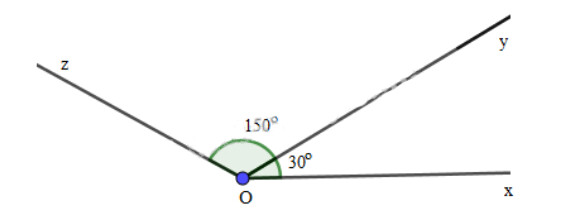
Góc $xOy$ và góc $xOz$ có tổng số đo bằng 180^ o nhưng không phải là hai góc kề bù, vì không kề nhau
b) Hai góc bằng nhau và có chung đỉnh không phải là hai góc đối đỉnh, chẳng hạn:
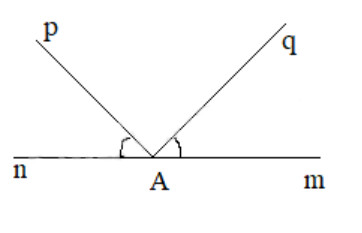
Góc $mAq$ và $nAp$ bằng nhau và có chung đỉnh nhưng không phải là hai góc đối đỉnh.
a) Hai góc có tổng số đo bằng 180^ o không phải là hai góc kề bù, vì 2 góc kề bù phải là 2 góc kề nhau và có tổng số đo bằng 180^ o , chẳng hạn:

Góc $xOy$ và góc $xOz$ có tổng số đo bằng 180^ o nhưng không phải là hai góc kề bù, vì không kề nhau
b) Hai góc bằng nhau và có chung đỉnh không phải là hai góc đối đỉnh, chẳng hạn:

Góc $mAq$ và $nAp$ bằng nhau và có chung đỉnh nhưng không phải là hai góc đối đỉnh.
Bài tập 3 trang 108
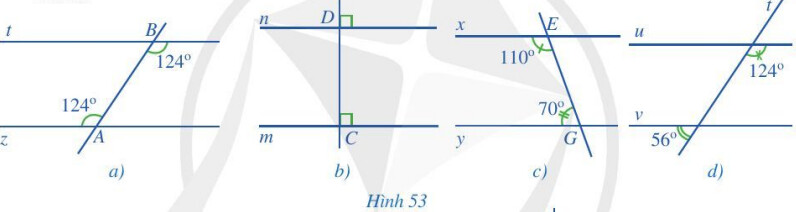
Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao?

Phương pháp giải:
+ Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ 2 góc kề bù có tổng số đo là 180 độ
+ Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ 2 góc kề bù có tổng số đo là 180 độ
Lời giải chi tiết:
a) Vì $\widehat{A_1}=\widehat{B_1}\left(=124^{\circ}\right)$. Mà 2 góc này ở vị trí so le trong nên z // $\mathrm{t}$
b) Vì $\widehat{D_1}=\widehat{C_1}\left(=90^{\circ}\right)$
Mà 2 góc này ở vị trí đồng vị nên $\mathrm{m} / / \mathrm{n}$
c) Vì $\widehat{E_1}+\widehat{E_2}=180^{\circ}$ ( 2 góc kề bù) nên
$110^{\circ}+\widehat{E_2}=180^{\circ} \Rightarrow \widehat{E_2}=180^{\circ}-110^{\circ}=70^{\circ}$
vì $\widehat{E_2}=\widehat{G_1}\left(=70^{\circ}\right)$. Mà 2 góc này ở vị trí so le trong nên $x / / \mathrm{y}$
d) Vì $\widehat{K_1}+\widehat{K_2}=180^{\circ}$ ( 2 góc kề bù) nên
$\widehat{K_1}+56^{\circ}=180^{\circ} \Rightarrow \widehat{K_1}=180^{\circ}-56^{\circ}=124^{\circ}$
vì $\widehat{H_1}=\widehat{K_1}\left(=124^{\circ}\right)$. Mà 2 góc này ở vị trí so le trong nên $u // v$
a) Vì $\widehat{A_1}=\widehat{B_1}\left(=124^{\circ}\right)$. Mà 2 góc này ở vị trí so le trong nên z // $\mathrm{t}$
b) Vì $\widehat{D_1}=\widehat{C_1}\left(=90^{\circ}\right)$
Mà 2 góc này ở vị trí đồng vị nên $\mathrm{m} / / \mathrm{n}$
c) Vì $\widehat{E_1}+\widehat{E_2}=180^{\circ}$ ( 2 góc kề bù) nên
$110^{\circ}+\widehat{E_2}=180^{\circ} \Rightarrow \widehat{E_2}=180^{\circ}-110^{\circ}=70^{\circ}$
vì $\widehat{E_2}=\widehat{G_1}\left(=70^{\circ}\right)$. Mà 2 góc này ở vị trí so le trong nên $x / / \mathrm{y}$
d) Vì $\widehat{K_1}+\widehat{K_2}=180^{\circ}$ ( 2 góc kề bù) nên
$\widehat{K_1}+56^{\circ}=180^{\circ} \Rightarrow \widehat{K_1}=180^{\circ}-56^{\circ}=124^{\circ}$
vì $\widehat{H_1}=\widehat{K_1}\left(=124^{\circ}\right)$. Mà 2 góc này ở vị trí so le trong nên $u // v$
Bài tập 4 trang 108
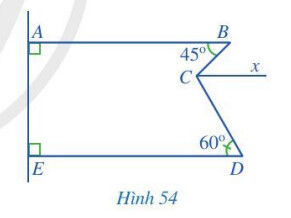
Quan sát Hình 54, trong đó $Cx$ song song với $AB$.
a) Tính số đo góc $BCx$.
b) Chứng minh rằng $Cx$ song song với $DE$.
c) Tính số đo góc $BCD$.
Phương pháp giải:
+ Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ Chú ý: 2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau
2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau
+ Sử dụng tính chất 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
+ Nếu tia $Om$ nằm trong góc $xOy$ thì $\widehat{x O m}+\widehat{m O y}=\widehat{x O y}$
+ Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ Chú ý: 2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau
2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau
+ Sử dụng tính chất 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
+ Nếu tia $Om$ nằm trong góc $xOy$ thì $\widehat{x O m}+\widehat{m O y}=\widehat{x O y}$
Lời giải chi tiết:
a) Vì $Cx$ // $A B$ nên $\widehat{A B C}=\widehat{B C x}$ ( 2 góc so le trong), mà $\widehat{A B C}=45^{\circ} \Rightarrow \widehat{B C x}=45^{\circ}$
b) Vì $A E \perp A B ; A E \perp E D$ nên $A B / / E D$ (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
Mà $\mathrm{Cx} / / \mathrm{AB}(\mathrm{gt})$
$\Rightarrow \mathrm{Cx} / / \mathrm{ED}$ (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)
c) Vì $Cx // ED$ nên $\widehat{E D C}=\widehat{D C x}$ ( 2 góc so le trong), mà
$\widehat{E D C}=60^{\circ} \Rightarrow \widehat{D C x}=60^{\circ}$
Vì tia $C x$ nằm trong góc $B C D$ nên
$\widehat{B C D}=\widehat{B C x}+\widehat{D C x}=45^{\circ}+60^{\circ}=105^{\circ}$
a) Vì $Cx$ // $A B$ nên $\widehat{A B C}=\widehat{B C x}$ ( 2 góc so le trong), mà $\widehat{A B C}=45^{\circ} \Rightarrow \widehat{B C x}=45^{\circ}$
b) Vì $A E \perp A B ; A E \perp E D$ nên $A B / / E D$ (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
Mà $\mathrm{Cx} / / \mathrm{AB}(\mathrm{gt})$
$\Rightarrow \mathrm{Cx} / / \mathrm{ED}$ (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)
c) Vì $Cx // ED$ nên $\widehat{E D C}=\widehat{D C x}$ ( 2 góc so le trong), mà
$\widehat{E D C}=60^{\circ} \Rightarrow \widehat{D C x}=60^{\circ}$
Vì tia $C x$ nằm trong góc $B C D$ nên
$\widehat{B C D}=\widehat{B C x}+\widehat{D C x}=45^{\circ}+60^{\circ}=105^{\circ}$
Bài tập 5 trang 108
Quan sát Hình 55, trong đó $mq // xt$
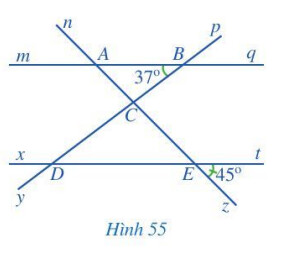
a) Kể tên các cặp góc đồng vị bằng nhau.
b) Tìm số đo các góc $BAC, CDE$.
c) Bạn Nam cho rằng: Qua điểm $C$ kẻ một đường thẳng $c$ song song với hai đường thẳng $mq$ và $xt$ thì sẽ tính được $\widehat{B C E}=82^{\circ}$. Theo em, bạn Nam nói đúng hay sai? Vì sao?
Phương pháp giải:
+ 2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau
+ Sử dụng tính chất 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
+ Nếu tia $Om$ nằm trong góc $x O y$ thì $\widehat{x O m}+\widehat{m O y}=\widehat{x O y}$
+ 2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau
+ Sử dụng tính chất 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
+ Nếu tia $Om$ nằm trong góc $x O y$ thì $\widehat{x O m}+\widehat{m O y}=\widehat{x O y}$
Lời giải chi tiết:
a) Các cặp góc đồng vị bằng nhau là: góc $m A n$ và $x E n$; góc $mAz$ và $xEz$; góc $nAq$ và $nEt$; góc $qAz$ và $tEz$; góc $pBq$ và $pDt$; góc $qBy$ và $tDy$; góc $mBy$ và $xDy$; góc $pBm$ và $pDx$
b) Vì $mq // xt$ nên $\widehat{B A C}=\widehat{z E t}$ ( 2 góc đồng vị) nên $\widehat{B A C}=45^{\circ}$.
Vì $mq // xt$ nên $\widehat{C D E}=\widehat{A B C}$ ( 2 góc so le trong) nên $\widehat{C D E}=37^{\circ}$.
c)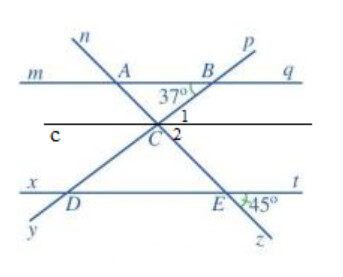
Bạn Nam nói đúng vì:
Vì $c // mq$ nên $\widehat{A B C}=\widehat{C_1}$ ( 2 góc so le trong) nên $\widehat{C_1}=37^{\circ}$
Vì $c // xt$ nên $\widehat{C E D}=\widehat{C_2}$ ( 2 góc so le trong) nên $\widehat{C_2}=45^{\circ}$
a) Các cặp góc đồng vị bằng nhau là: góc $m A n$ và $x E n$; góc $mAz$ và $xEz$; góc $nAq$ và $nEt$; góc $qAz$ và $tEz$; góc $pBq$ và $pDt$; góc $qBy$ và $tDy$; góc $mBy$ và $xDy$; góc $pBm$ và $pDx$
b) Vì $mq // xt$ nên $\widehat{B A C}=\widehat{z E t}$ ( 2 góc đồng vị) nên $\widehat{B A C}=45^{\circ}$.
Vì $mq // xt$ nên $\widehat{C D E}=\widehat{A B C}$ ( 2 góc so le trong) nên $\widehat{C D E}=37^{\circ}$.
c)

Bạn Nam nói đúng vì:
Vì $c // mq$ nên $\widehat{A B C}=\widehat{C_1}$ ( 2 góc so le trong) nên $\widehat{C_1}=37^{\circ}$
Vì $c // xt$ nên $\widehat{C E D}=\widehat{C_2}$ ( 2 góc so le trong) nên $\widehat{C_2}=45^{\circ}$
Cảm ơn bạn đọc đã theo dõi bài viết của HocThatGioi về Bài tập cuối chương IV. Góc – Đường thẳng song song trang 108 SGK Toán 7 Cánh diều tập 1. Hy vọng các bạn đã nắm được toàn bộ kiến thức của bài học này. Chúc các bạn ôn tập thật tốt!





